|
|
Относительные уровни издержек на предприятиях 8 глава
Если бы эти затраты были равными для выпивки и закуски, то и на одно, и на другое пришлось бы по
откуда
х= 12 л выпивки или 12 кг закуски. Следовательно: 1) Было закуплено 12 л выпивки и 12 кг закуски. 2) Стоимость выпивки равна 12 х 20 = 240 у. д. ед., стоимость закуски – 12 х 10 = 120 у.д.ед. 3) Всего потрачено 240 + 120 = 360 у. д. ед.
113. Обозначим через х фактическую цену продажи партии товара. При этом цена его покупки будет
Итак, условие задачи можно записать следующим образом:
откуда
Следовательно: 1) Партия товара была продана за 200 тыс. у. д. ед., а единица товара стоила
2) Цена покупки партии товара равна
114. Обозначим через х сумму, выделенную фирмой для закупки компьютеров, через у – равные количества компьютеров обоих видов (при первом варианте закупки); через z – количество компьютеров вида «МА» и w – вида «МБ» (при втором варианте закупки). При этом условие задачи можно записать так: первый вариант закупки:
второй вариант закупки:
Из уравнения (1) следует, что общее количество закупленных компьютеров по первому варианту равно:
Из уравнения (2) следует, что общее количество закупленных компьютеров по второму варианту равно:
По второму, более выгодному, варианту может быть закуплено компьютеров больше, чем по первому, на
Иными словами, при закупке по второму варианту фирма дополнительно (по сравнению с первым вариантом) бесплатно получает на каждые 120 компьютеров еще один. 115. Обозначим через х, у, z количество купленных компьютеров, телефонов и столов соответственно. Тогда условие задачи можно записать так:
или после умножения левой и правой частей на 4:
Вычитая (2) из (1), получим:
откуда
Из (3) следует, что, во-первых, х может быть равен только 2, так как z и x должны быть целыми положительными числами, во-вторых, х не может быть равен 1, так как при этом z становится равным 53, что противоречит условию (всего куплено 30 предметов), и, в-третьих, х не может быть больше 2, так как при этом z становится отрицательным. Итак, х = 2 единицам. Из (3) следует, что z = 90 – 37 x 2=16 единиц, из (2) следует, что у = 30 – 2 – 16 =12 единиц. 116. Обозначим через х и у стоимость единиц товара А и Б соответственно. Тогда условие задачи можно записать так:
Решим систему из двух уравнений с двумя неизвестными, для чего умножим правую и левую часть уравнения (1) на 7, а уравнения (2) на 5:
Вычитая второй результат из первого, получим:
Из (1) следует, что
117. Обозначим через х и у соответствующее количество компонентов «Радость» и «Сладость» в 50 литрах коктейля. Тогда условие задачи можно будет записать так:
Решим систему из двух уравнений с двумя неизвестными. Подставляя из (2) в (1), получим:
откуда
Из (2) следует, что
Следовательно, в коктейле
напитка «Радость»
и напитка «Сладость».
118.Обозначим через х количество приобретенных шин (или аккумуляторов), а через у – количество непроданных аккумуляторов. Тогда количество непроданных шин составит 7 - у, количество проданных аккумуляторов х - у, количество проданных шин х - (7 - у). Стоимость покупки равна:
Стоимость продажи (с учетом прибыли) равна:
По условию задачи стоимость продажи равна стоимости покупки:
или после преобразований
Решая последнее (так называемое диофантовое) уравнение, следует иметь в виду следующие ограничения: 1) х и у – целые числа, 2) х и у – положительны, 3) х и у – меньше 7. Указанным ограничениям отвечают только значения у, равные 5 или 2 (при всех других значениях у значения х не будут целыми числами); у = 2 не подходит, так как из (*) при этом нарушается условие
продажи шин парами (33 не делится на 2). Следовательно, у = 5. При этом стоимость покупки составляет Зх = 3 х 44 = 132 тыс. у. д. ед. Нетрудно убедиться, что при оставшихся непроданных пяти аккумуляторах и двух шинах их стоимость составляет:
что как раз равно 0,1 от стоимости покупки, т. е. прибыль действительно равна 10 %. 119. Обозначим стоимость первой квартиры при ее покупке через х, а второй – через у. Тогда условие задачи можно записать так:
Из (1) следует, что
Подставляя значение у в (2), получим:
откуда х = 180 тыс. у. д. ед.
120. Обозначим через х деньги родителей, а через у деньги детей. Тогда условие задачи можно записать так:
Из (1) следует, что
Подставляя значение у в (2), получим:
или после преобразований
2) Цена участка по условию задачи равна остающейся у родителей или у детей сумме денег
Значит, она равна 121.Вначале рассчитаем процент и вес сухого остатка в товаре. При первом замере жидкости сухой остаток составил 1 % и весил 1 т. При втором замере – соответственно 4 % и снова 1 т (вес сухого остатка не меняется). Интересующий нас вес всего товара (100 %) при втором замере (х) находим из очевидной пропорции:
Откуда х = 25т. За этот товар следует заплатить 25т х 300 тыс. у. д. ед. = 7,5 млн у. д. ед. 122. Задача допускает несколько решений. Одно из наиболее интересных следующее. Фирма Б заключает с фирмой В контракт на поставку лишь половины товара, получаемого от фирмы А. Тогда сумма этого контракта будет 100 млн руб. и неустойка фирме В составит лишь 10 млн руб. В случае, если фирма А сорвет контракт, фирма Б ничего не потеряет, выплачивая фирме В только то, что получит от фирмы А. Если же фирма А сделает нормальную поставку, фирма Б заключит с фирмой В контракт и на вторую половину товара. 123. Будем рассуждать следующим образом: 1) За сколько дней Иванов израсходует 10 бочек?
10 x 14 = 140 дней.
2) Сколько бочек за эти же 140 дней израсходовали бы Иванов и Петров совместно?
3) Сколько бочек за эти 14 дней израсходовал бы Петров?
14 - 10 = 4 бочки.
4) За сколько дней Петров израсходовал бы одну бочку?
124. Нужда – это нехватка определенного круга предметов или услуг (например, нужда в пище, одежде, квалифицированной медицинской помощи). Потребность – это нужда в конкретном товаре. Спрос – это потребность, подкрепленная возможностью покупателя заплатить за товар.
125. В предвкушении еды нас интересует не величина яблока, а его объем. Отношение объемов шаров пропорционально отношению кубов их радиусов. В нашей задаче это отношение равно:
Следовательно, по объему первое яблоко больше второго примерно в 2 раза. А стоит оно всего в 1,5 раза дороже. Значит, такое яблоко покупать выгоднее. 126. Руководствуясь теми же соображениями, что и в решении задачи 125, составим отношение объемов яиц:
Следовательно, второе яйцо выгоднее. Уместно отметить, что соображения, высказанные при решении двух последних задач, справедливы по отношению к любым фруктам или овощам шарообразной или близкой к ней формы: чем они крупнее, тем выгоднее. 127. Для решения задачи вообразим, что диаметр крупинок муки крупного помола больше, чем мелкого, скажем, в 10 раз. Увеличим мысленно крупинки мелкой муки до размера крупинок крупной. Одновременно увеличим во столько же раз и размер мешка. Тогда объем его вырастет в 10х 10 х 10= 1000 раз. Во столько же раз увеличится и вес муки. И если мы теперь отсыпем из этого огромного мешка один наш мешок, то он составит одну тысячную веса большого мешка. Но ведь это и будет мешок муки крупного помола. И вес его окажется точно таким же, как и у мешка муки мелкого помола. Следовательно, одинаковые по объему мешки муки мелкого и крупного помола равны и по весу.
128. 1) Если на все деньги купить только радиоаппаратуру, то ее окажется 480 тыс. у. д. ед.: 30 тыс. у. д. ед. = 16 единиц. Но при этом экспедитор нарушает задание – купить товары всех трех видов. Поэтому ему придется ограничиться 15-ю единицами радиоаппаратуры, оставив деньги на более мелкие покупки (одежду и бытовую технику). 2) Допустим, мелкие покупки уже сделаны. Тогда если бы радиоаппаратура стоила по 10 тыс. у. д. ед. за единицу, то за 15 единиц пришлось бы заплатить 150 тыс. у. д. ед. (менее 200 тыс. у. д. ед.) и осталось бы явно более 28 тыс. у. д. ед. (480 - 200) на доплату стоимости радиоаппаратуры – по 20 тыс. у. д. ед. (30 - 10) за каждую единицу. Следовательно, куплено было бы более 14 единиц (280 тыс. у. д. ед.: 20 тыс. у. д. ед.). Итак, можно купить радиоаппаратуры не более 15 единиц, но более 14, т. е. 15 единиц. За 15 единиц радиоаппаратуры будет заплачено 450 тыс. у. д. ед. и, таким образом, на мелкие покупки останется 30 тыс. у. д. ед. (480 - 450). 3) На оставшиеся 30 тыс. у. д. ед. должно быть сделано 5 (20 - 15) мелких покупок двух видов. Если бы бытовая техника стоила 10 тыс. у. д. ед. за единицу, то 5 ее единиц обошлись бы в 50 тыс. у. д. ед., т. е. пришлось бы переплатить сверх задания 20 тыс. у. д. ед. (50 - 30) из-за переплаты по 5 тыс. у. д. ед. (10-5) на каждой единице. Поэтому приходится покупать не 5 единиц бытовой техники, а 4 – всего на 20 тыс. у. д. ед. (4 x 5 тыс. д. ед.). 4) На оставшиеся 10 тыс. у. д. ед. (30 - 20) можно купить третий вид товара – одежду. Этого как раз хватит на 1 единицу одежды. Итак, экспедитор покупает: 15 единиц радиоаппаратуры, 1 единицу одежды и 4 единицы бытовой техники.
129. Не только не переоценивает, но даже преуменьшает. Возьмем в руки самый подробный каталог товаров. Вряд ли он будет иметь более 1000 страниц. Откроем его посередине, на 500-й странице, и зададим 1-й вопрос: «Задуманный товар находится на этой странице или после нее?» Получив ответ, мы уменьшаем количество претендентов на задуманный товар ровно в 2 раза. Продолжая таким же образом «половинить» каталог, на 10-м вопросе мы дойдем до одной его страницы, на которой и будет искомый товар. Далее подобным же путем найдем один из двух столбцов, в которых располагаются товары (11-й вопрос). В столбце вряд ли будет более 10 товаров. Чтобы «споловинить» и их, потребуется еще максимум 4 вопроса. Итого 15 вопросов, и задача решена. 130. Действие чашечных весов основано на принципе рычага. Если правое плечо весов имеет длину П, левое – Л, и грузы, которые мы взвешиваем на правой и левой чашках, равны соответственно Рп и Рл, то должно действовать известное из физики равенство:
Поскольку весы неисправны, при первом взвешивании вес гири Г соответствует хкг товара, а при втором взвешивании – укг товара. Равновесие наступает при следующем равенстве: П х Г = Л х х – для первого взвешивания; Л х Г = П х х – для второго взвешивания. Из этих соотношений следует, что
При этом общий вес товара равен:
Из алгебры известно, что
(кроме случаев, когда
Значит, фактический вес товара больше, чем полученный в результате предложенного способа взвешивания.
131. После первой замены бензина на колонке оставалось 36 - 12 = 24 т высококачественного бензина. При этом в одном литре смеси высококачественный бензин составлял При второй замене в 9 т израсходованной смеси содержалось А в одном литре смеси – соответственно
После третьей замены в 8 т израсходованной смеси содержалось 14 т из 36 – это 39 % высококачественного бензина и 61 % (100 - 39) низкосортного. 132. 150 т. 133. Пожалуй, дешевле всего будет перенести увеличенное изображение небольшого часового циферблата на экран, помещенный на башне, с помощью оптического проектора. 134. Обозначая стоимость клипсов через Кл, броши – Бр, кольца – Кол и заколки – Зак, можно по условию задачи составить следующие два уравнения:
Совместное решение уравнений (1) и (2) даст искомый результат:
135. Предположим, вторая крестьянка имела в К раз больше яиц, чем первая. Так как они обе выручили одинаковые суммы, из сделанного предположения следует, что первая продавала яйца в К раз дороже, чем вторая. Если бы перед торговлей они поменялись яйцами, то у первой было бы в К раз больше яиц, чем у второй, и она продавала бы их в К раз дешевле. При этом она выручила бы денег в К х К = К2раз больше второй. Из этого следует отношение их выручек:
Деля 100 яиц в отношении 3 : 2, получим, что у первой крестьянки было 60 яиц, а у второй - 40. 136. Норма прибыли (рентабельность) рассчитывается по формуле:
где НРПР – норма прибыли, ПР – прибыль, З – затраты.
137. Из формулы, приведенной в решении задачи 136, следует:
где В –выручка. Откуда
138. Норма накопления (НН) рассчитывается по формуле:
где Пнак – масса прибыли, направленная на накопление; Ппот – масса прибыли, направленная на потребление.
139. По формулам, приведенным в решении задач 136 и 137:
140. По формулам, приведенным в решении задачи 136, следует:
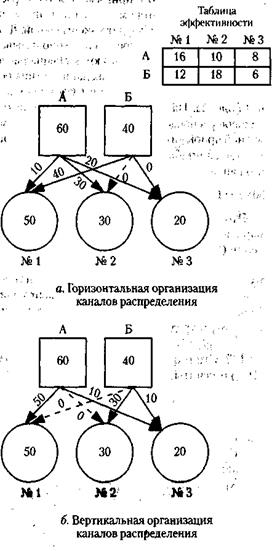
141. При горизонтальной организации каналов распределения товаров (см. рис.) каждый из производителей стремится направить свой товар по каналам, обеспечивающим наибольшую прибыль. При этом интересы производителей сталкиваются: один и тот же канал может оказаться привлекательным для обоих производителей, а пропускная способность каждого канала ограничена. В итоге стихийно складывается распределение, один из возможных вариантов которого показан на рисунке. При этом производитель товаров А получает прибыль, реальную сумме произведений единиц товара, направляемых каждому из потребителей, на соответствующие эффективности.
Прибыль производителя товара А = 10 х 16 + 30 x 10 + 20 x 8 = 620. Аналогично рассчитывается прибыль производителя товара Б : 40 х 12 + 0 х 18 + 0 х 6 = 480. Производитель товара А оказался в явном выигрыше. Казалось бы, что может быть для него лучше? Не будем, однако, торопиться с выводами. Рассмотрим вертикальную организацию каналов распределения товаров (см. рис.). В этом случае распределение товаров осуществляется в интересах не отдельного производителя товара, а системы в целом: принимается такое распределение, при котором суммарная прибыль обоих производителей будет максимальной. Для нахождения такого распределения (оно называется оптимальным) используются специальные методы. В простейших задачах данного типа решение может быть получено и глазомерно, путем подбора. На рисунке показано такое оптимальное распределение. Найдем величину суммарной прибыли обоих производителей товаров. Общая прибыль производителей товаров А и Б равна:
50 x 16 + 0 x 10 + 10 x 8 + 0 x 12 + 30 x 18 + 10 x 6 = 1480.
Это существенно (на 35 %) больше, чем суммарная прибыль при горизонтальном распределении (620 + 480 = 1100). Разделив соответствующую вертикальному распределению общую прибыль пополам (1480 : 2), получим 740 единиц, что значительно больше, чем прибыль победителя при горизонтальном распределении товара (740 - 620 = 120). 142.Стоимость оптимальной партии товара (Попт) рассчитывается по формуле:
где Г – годовая стоимость заказа, Изг – стоимость издержек изготовления партии товара, Хр – стоимость издержек хранения товара.
Объем партии товара (Об) при этом равен:
143.1000 у. д. ед. стоит 1 кг орехов или 400 г ядер. Следовательно, 1 кг ядер должен стоить в 2,5 раза (1000 г : 400 г) дороже, т. е. 2500 у. д. ед. Значит, выгоднее покупать неочищенные орехи.
144. Можно обойтись всего двумя взвешиваниями. Первое: положить на каждую чашку весов по 3 любые монеты; если монеты уравновесятся, значит, фальшивая в оставшейся тройке; если одна из чашек окажется легче – искомая монета в ней. Второе: из тройки монет, в которой обнаружена фальшивка, две любые монеты разложить по чашкам весов; если монеты уравновесятся, значит, фальшивая – оставшаяся; если одна из монет окажется легче – она и есть фальшивая. Итак, взвешивание обойдется в 200 у. д. ед.
145. Один делит пополам, второй выбирает свою часть. (Кто делит, а кто выбирает, определяется по жребию.)
146. Вначале по жребию определяется, кто будет делить (это может быть один или несколько человек). Производится раздел, который утверждается на общем собрании товарищества. Полученные части распределяются по жребию. (Описанная процедура раздела должна быть заранее одобрена всеми членами товарищества.)
147. Обозначим первоначальный капитал через х
148. 5 млн руб. и 2 млн руб.
149.1) Поскольку общий капитал без первого предпринимателя на 50 тыс у. д. ед. больше, чем без второго, то капитал первого на 50 тыс. у. д. ед. меньше, чем второго. 2) По тем же соображениям капитал третьего предпринимателя на 50 тыс. у. д. ед. больше, чем второго. 3) Следовательно, если сложить капиталы первого, второго и третьего предпринимателей, то разница в капиталах первого и второго взаимно компенсируется и общая сумма будет равна трехкратному капиталу второго предпринимателя. 4) Но сумма капиталов первого, второго и третьего предпринимателей – это и есть общий капитал без четвертого, который, как известно, равен 750 тыс. у. д. ед. Следовательно, капитал второго предпринимателя, в соответствии с п. 3, равен 750 тыс. у. д. ед.: 3 = 250 тыс. у. д. ед. 5) Следовательно, капитал первого равен 200 тыс. у. д. ед. (на 50 тыс. у. д. ед. меньше, чем у второго), капитал третьего равен 300 тыс. у. д. ед. (на 50 тыс. у. д. ед. больше, чем у второго). 6) Поскольку, как следует из п. 1 и 2, капитал четвертого предпринимателя на 50 тыс. у. д. ед. больше, чем третьего, он равен 350 тыс. у. д. ед.
150. 1) По формуле сложных процентов (проценты на проценты) завещанный капитал (В) через С лет составит К:
где п – проценты на капитал, е – основание натурального логарифма, равное 2,731828. Подставляя в формулу соответствующие значения, получим:
С помощью таблицы сложных процентов, помещенной в приложении, получим: С = 1000 х 131,539 = 131 539 фунтов стерлингов. 2) После выделения 100 тыс. фунтов стерлингов на постройку общественных зданий останется: 131 539 - 100 000 = 31 539 фунтов стерлингов. 3) Еще через 100 лет эта сумма составит (с учетом сложных процентов): 31 539 х 131 539 = 4 147 380 фунтов стерлингов. 4) После вычета из этой суммы 3 млн фунтов стерлингов бостонским жителям достанется: 4 147 380 - 3 000 000 = 1 147 380 фунтов стерлингов. По данной формуле рассчитана таблица сложных процентов, помещенная в приложении к решениям.
151. Четыре брата и три сестры. 152. Решение данной задачи неоднозначно и зависит от толкования воли завещателя. 1) Если считать волей завещателя дать сыну наследство вдвое больше, чем матери ( 2) Если же считать волей завещателя также желание оставить матери не менее |
|

 у. д. ед. Исходя из этого, условие задачи можно записать так:
у. д. ед. Исходя из этого, условие задачи можно записать так: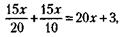
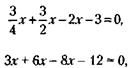
 . Если бы товар был куплен на 30 % дешевле, цена покупки составила
. Если бы товар был куплен на 30 % дешевле, цена покупки составила  . Продажа этого товара по цене на 60 % дороже цены покупки была бы равна в этом случае
. Продажа этого товара по цене на 60 % дороже цены покупки была бы равна в этом случае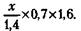

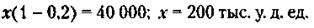
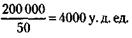
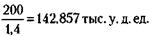
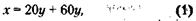
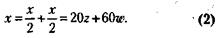


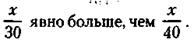
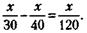
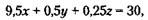

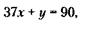

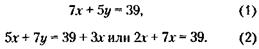
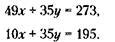

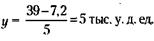
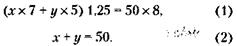
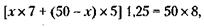
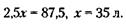
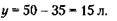
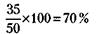
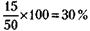
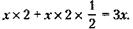
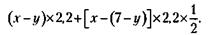
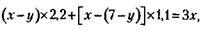
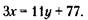
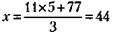
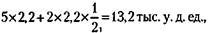

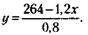
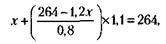
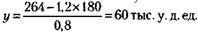

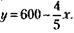
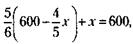

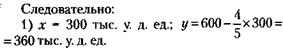

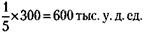
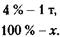
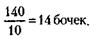
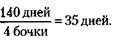

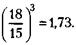
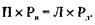

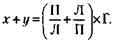

 )* .
)* .
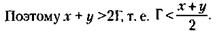
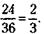
 высококачественного бензина. Следовательно, в оставшемся на колонке бензине высококачественного было 24 - 6= 18 т.
высококачественного бензина. Следовательно, в оставшемся на колонке бензине высококачественного было 24 - 6= 18 т.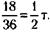
 высококачественного бензина. Следовательно, в оставшемся на колонке бензине высококачественного было 18 - 4= 14т.
высококачественного бензина. Следовательно, в оставшемся на колонке бензине высококачественного было 18 - 4= 14т.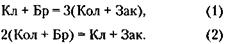
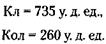
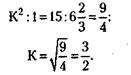
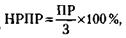
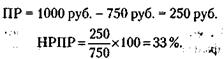


 Н,
Н,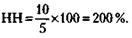
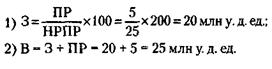
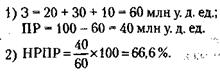
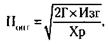
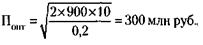
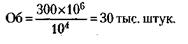
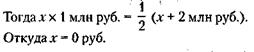
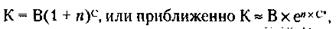
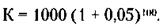
 и
и  ), а дочери – вдвое меньше, чем матери (
), а дочери – вдвое меньше, чем матери (  ), то наследство следует разделить в пропорции: дочери – 1 часть, матери – 2 части, сыну – 4 части, т. е.
), то наследство следует разделить в пропорции: дочери – 1 часть, матери – 2 части, сыну – 4 части, т. е. 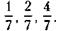
 меньше
меньше  ). Тогда дочь получает
). Тогда дочь получает  , сын
, сын  , а мать
, а мать  наследства.
наследства.