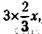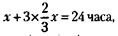|
|
Относительные уровни издержек на предприятиях 9 глава153.Обозначив искомый процент по вкладам через х, по формуле сложных процентов (см. решение задачи 150) получим:
Логарифмируя с помощью таблицы логарифмов, получим:
Антилогарифм 1+ х = 1,042. х = 4,2 % 154.Норма процента (НП) равна:
где Д – доход, Сс – величина ссуды.
155. Величина ссуды (Сс) равна (см. решение задачи 154):
156. Величина дохода (Д) равна (см. решение задачи 154):
157. Банковская прибыль (БП) равна:
158.
159. 1) Положив деньги в банк, можно получить за год 8 тыс. руб. (8 %от 100 тыс. руб.). 2) Можно купить 4 привилегированные акции и получить 10 тыс. руб. дивидендов (10 % от 4 х 20 тыс. руб.). 3) Можно купить обыкновенные акции. Доход по ним определим исходя из следующих соображений. После первоочередной выплаты по всем привилегированным акциям 200 тыс. руб. (80 х 25 х 10 %) на выплату по обыкновенным акциям останется 800 - 200 = 600 тыс. руб. Следовательно, на каждую обыкновенную акцию придется 6 тыс. руб. дивидендов Если купить на все деньги 5 обыкновенных Следовательно, самое выгодное вложение капитала – покупка обыкновенных акций. 160.Суммарный капитал равен 150 млн руб. Прибыль на капитал равна Выплата за ссуду составит 5 млн руб. Предпринимательский доход равен 45 - 5 = 40 млн руб.
161. В соответствии с теорией статистических решений среднеожидаемая прибыль равна:
Следовательно: – при вложении капитала в кинофильм
– при вложении капитала в торговлю
Таким образом, выгоднее вкладывать капитал в торговлю.
162. При вложении денег один раз в год доход равен 150 тыс. руб. При вложении денег два раза на 6 месяцев (с учетом вложения дохода за первое полугодие) доход равен 172,25 тыс. руб. При вложении денег четыре раза на 3 месяца (с учетом вложения доходов за каждый квартал) доход равен 185,6 тыс. руб. Следовательно, выгоднее всего вкладывать деньги на 3 месяца.
163. 1) Издание книги будет безубыточным (точка безубыточности – ТБ) при тираже:
2) При цене одной книги 11 у. д. ед.:
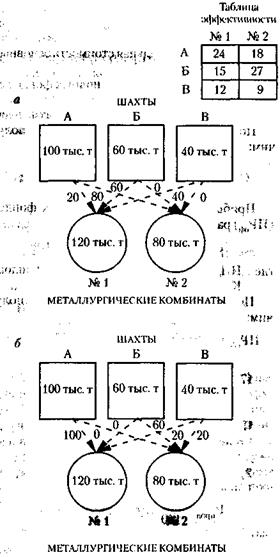
164. Один из наиболее простых и очевидных вариантов глазомерного решения показан на рисунке а. Общая стоимость перевозки руды при этом будет составлять:
Однако методами математического планирования можно разработать значительно более экономный план перевозки руды (см. рис. б). В данном случае это можно сделать и путем простого перебора вариантов. При таком оптимальном плане общая стоимость перевозок уменьшится примерно на 25 % и составит:
165.Обозначим закупочную цену единицы товара через х. Тогда оптовая цена составит 1,2х, розничная цена – 1,3 (1,2х), а после ее снижения - 0,9 [1,3(1,2х)]. По условию задачи эта последняя цена равна 100 у. д. ед., т. е. 0,9 х 1,3 х 1,2х = 100.
166. Обозначим цену товара до и после ее снижения через х и у соответственно. Тогда условие задачи запишется так:
Из (1) следует:
Подставляя значение у в (2), получим:
167. Планируемый доход (Д) рассчитывается по формуле:
где К – количество выпущенных лотерейных билетов; Б – стоимость одного лотерейного билета; С – количество счастливых билетов; В – величина выигрыша на один счастливый билет.
Отсюда
С учетом того, что требуемый доход должен составить
При этом вероятность выигрыша на 1 билет (Рв) равна:
168. Для того чтобы Рв = 1 %, или 0,01, количество счастливых билетов С должно вырасти в десять раз и составить 9870. Тогда Д = 107 х 103 - 9870 х 10-7 = -88,7 х 109 руб. Иными словами, убыток составит около 89 млрд руб.
169. Расчет производится по формуле теории вероятностей:
где N – требуемое количество билетов, из которых хотя бы один (не менее одного) выиграет, Руд – вероятность удачи, выигрыша хотя бы одного из купленных билетов, Рв – вероятность выигрыша в лотерею на один билет.
170. Обозначая через А и П стоимости автомобиля и прицепа, получим следующие очевидные равенства:
Складывая левые и правые части равенств, получим:
Следовательно, А = 1,4 млн у. д. ед., П = 0,1 млн у. д. ед. 171. Прибыль (ПР) рассчитывается по формуле:
где В – выручка, МЗ – материальные затраты, HP – накладные расходы, ЗЗП – затраты на зарплату. Подставляя соответствующие цифры, получим: ПР = 100 000 - (50 000 + 10 000 + 10 000) = 30 000 у. д. ед. Налог на прибыль (НПР) равен 32 % от ПР, т. е. 9600 у. д. ед. Чистая прибыль (ЧПР) равна: ПР - НПР = 30 000 - 9600 = 20 400 у. д. ед. 172. Остаточная стоимость основных фондов (ОС) рассчитывается по формуле:
где ПС –первоначальная стоимость основных фондов, ПИ –процент износа основных фондов за 1 год, СИ – срок использования основных фондов. Подставляя соответствующие цифры, получим:
Прибыль от реализации основных фондов (ПРоф) рассчитывается по формуле:
где ПЦ – продажная цена основных фондов, К – индекс инфляции. Подставляя соответствующие цифры, получим:
173. 1) Общие затраты составляют: 60 + 50 + 20 + 10 = 140 у. д. ед.
Прибыль равна:
200 - 140 = 60 у. д. ед.
2) Рентабельность продукции равна:
174. На 10 000 у. д. ед. (в том числе 6000 у. д. ед. стоимость шапки и 4000 у. д. ед.– сдача). 175. Плата за кредит (Кр) рассчитывается по формуле:
где В – величина суммы кредита (первоначального вклада в Сбербанк), П – процентная ставка, С – срок кредита. Подставляя соответствующие цифры, получим:
176. По формуле сложных процентов (см. решение задачи 150) через два года вклад будет составлять:
177. По формуле сложных процентов (см. решение задачи 150) через С лет вклад будет составлять:
Логарифмируя, получим:
откуда
По приближенной формуле:
178. В первом круге операции участвует 1 покупатель, во втором – 2, в третьем – 4... в 11 круге – 1024 покупателя. Еще через 10 кругов чисто участников операции станет более миллиона, в городе не останется покупателей, и те, у кого талоны оказались нереализованными, уже нe сумеют их продать. Вот эти-то незадачливые покупатели и оплачивают разницу в цене продажи и покупки товара.
179. За 30 дней мне заплатят 30 х 100 тыс. долларов = 3 млн долларов. Я же заплачу: за 1-й день – 1 цент, за 2-й день – 2 цента, за 11-й день – 10 долларов 24 цента, за 21-й день – 10 485 долларов 76 центов, за 30-й день – 5 368 709 долларов 12 центов. За 30 дней общая сумма, которую мне придется выплатить, составит 10 737 418 долларов 3 цента, т. е. примерно в три раза больше того, то я получу.
180. Обозначим через х количество сотен тысяч рублей, указанных в чеке, а через у количество тысяч рублей, указанных в чеке. Тогда общая сумма, указанная в чеке, будет равна (х х 100 + у) тыс. руб., а сумма, выданная клиенту, – (х + l00у) тыс. руб. Условие задачи при этом будет выглядеть так:
Преобразуя его, получим первое уравнение с двумя неизвестными:
Второе уравнение составляется исходя из следующего, не очень заметного обстоятельства, содержащегося в условии задачи: сумма в тысячах рублей, превращенная в сумму в сотнях тысяч рублей, после того как из нее вычитаются три с половиной сотни тысяч, должна при делении на число сотен тысяч (теперь это тысячи рублей) дать без остатка число 2. Вот как можно записать это условие с учетом того, что число сотен тысяч нужно, кроме трех, уменьшить еще на единицу (из которой вычитается половина сотни тысяч):
Отсюда получаем второе уравнение:
Совместное решение уравнений (1) и (2) дает ответ задачи:
181. Все зависит от того, сколько было денег вначале. Если в начале сделки вы располагали всего 2100 руб., то к концу первого месяца их станет 2100 х 2 - 2400 = 1800 руб., к концу второго месяца: 1800 х 2 - 2400 = 1200 руб., к концу третьего: 1200 х 2 - 2400 = 0 руб. И на этом сделка закончится с вашим убытком в 2100 руб. Нетрудно сообразить, что для успеха сделки ваш первоначальный вклад должен быть больше, чем та сумма, которую вы должны ежемесячно выплачивать банку. Математически это условие запишется так. Обозначим необходимую для второй сделки сумму первоначального вклада через х. Тогда х х 2 - 2400 > х, откуда видно, что х > 2400 руб.
182. 1) На 50%. 2) На 100%.
183. Извлечение корня квадратного из обеих частей выражения (**) допускает два решения. Первое решение (***) неверно. Верно второе решение: x-z = -(y-z), из которого следует, что х- 2 = z- у, а это не приводит к ошибке. Действительно, так как z и у положительны, то из равенства (*) следует, что
Но это означает, что в случае 1) х - у > 0, у - z < 0 и равенство (***) неверно, или в случае 2) х - z < 0 х - у > 0 и равенство (***) также неверно. Второе же решение не противоречит ни одному из этих случаев.
184. Обозначая цену товара до и после снижения через х1 и х2, получим следующее очевидное соотношение:
из которого видно, что х1 = 100 руб.
185. Примем первоначальную цену товара и зарплату в 1000 руб. Тогда новая цена товара будет 150 000 руб., а новая зарплата – 100 000. Реальная зарплата при этом уменьшилась на
186. Вначале рассчитывается, каков процент неучастия объединения во внешнеэкономических операциях со всеми странами, кроме США: с Великобританией это 20 % (100 % - 80 %), с Японией – 15 %, с Германией – 10 %. Затем находится суммарный процент в операциях со всеми этими странами, который равен 20 % + 15 % + 10 % = 45 %. Этот процент следует вычесть из процента участия в операциях США, что и будет ответом по данной задаче: 60 % - 45 % = 15 %.
187. Надо разделить 25 руб. на 50 частей (49 + 1). Это даст 25 : 50 = 0,5 руб., что явится меньшей из двух частей. Большая часть будет содержать 49 частей и составит 0,5 х 49 = 24,5 руб.
188. По формуле теории вероятностей необходимое количество операций (N) будет равно:
189. По формулам, приведенным в решении задачи 171: 1) Д = 100+ 50 =150 млн руб. 2) ОПР = 150 - 90 = 60 млн руб. 3) НПР = 35 % от ОПР = 21 млн руб. 4) ЧПР = 60-21 = 39 млн руб. 5) Взносы в бюджет из фонда оплаты труда (ВОТ): ВОТ = 39 % от 50 млн руб. = 19,5 млн руб.
190. 1) 100 % + 20 % (это выручка + НДС) = 240 млн руб. Откуда НДС = 40 млн руб. 2) Предприятие уплатит НДС по формуле:
Следовательно, 16,67 % от (300 - 240) млн руб. = 10 млн руб.
191. Средняя месячная оплата труда менеджера составляет:
За 7 месяцев зарплата в деньгах составит: 52 тыс. у. д. ед. х 7 мес. = 364 тыс. у. д. ед. Но за это время менеджер уже получил 240 тыс. у. д. ед. Следовательно, премия оценена в 364 - 240= 124 тыс.у.д.ед.
192. Выход существует. Ведь условия соглашения касаются лишь выигрыша первого дела. Значит, если учитель подаст в суд повторно, то оговоренное условие уже не будет действовать, и он сможет получить деньги по решению суда.
193. Для быстрого устного решения задачи нужно сообразить, что сумма последовательных чисел от 1 до 100 складывается из следующей суммы пар чисел: 1-го с последним, 2-го с предпоследним и т. д. Каждая такая пара равна в сумме 101, а всего таких пар 50. Итак, нужно просто у множить 101 на 50, что легко сделать устно: 101 х 50 = 5050. 194.80 % от 25 % равно 20 %.
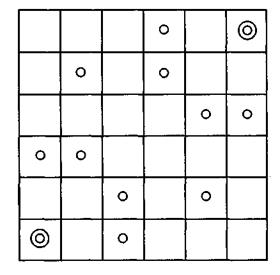
196.12 павильонов (включая два административных). Решение задачи ясно из рисунка.
197. Эту задачу удобно начинать решать с конца. Обозначим через х конечные капиталы каждого из партнеров. Тогда к началу третьей операции (в этом месяце) текущие капиталы партнеров А, Б, В должны были соответственно составить К началу второй операции (месяц назад) текущие капиталы партнеров А, Б, В соответственно составляли А к началу первой операции (два месяца назад) начальные капиталы партнеров А, Б, В выглядели так:
При этом потери партнера А равны:
Следовательно, начальный капитал партнера А равен:
партнера Б
партнера В:
198. Обозначим через х и у вложения в операции А и Б соответственно. Тогда условие задачи можно записать так:
Решим систему из двух уравнений с двумя неизвестными. Из (1) следует: у = 8 - х. Подставляя значение у в(2), получим:
откуда
Решая квадратное уравнение по стандартной формуле, получим:
х1 = 6 (х2 не подходит, так как при нем х < у, что противоречит условию). Следовательно, сумма вложения в операцию А равна 6 млн у. д. ед., в операцию Б: 8 – 6 = 2 млн у. д. ед. 199. Обозначим через х возраст сооружения Б. Тогда условие задачи можно записать так:
Следовательно: возраст сооружения А – 9 лет, возраст сооружения Б – 3 года, возраст сооружения В – 45 лет, возраст сооружения Г – 3 года, возраст сооружения Д – 70 лет. 200. Обозначим через х количество дней, когда предприниматель был здоров, а через у – нездоров. Тогда условие задачи можно записать так:
Здесь х и у – целые положительные числа. Произведем перебор х. При х = 1 выражение (*) будет таким:
откуда
(такое дробное значение у не подходит). При х = 2 выражение (*) будет таким:
откуда
(это значение у подходит). Итак: 1) Количество дней, когда предприниматель был здоров, равно 2, нездоров – 8. 2) Действие договора продолжалось 2 + 8 = 10 дней. 201. Интерполируя с помощью таблицы сложных процентов, получим:
Откуда х1 = 12 месяцев.
202. Интерполируя с помощью таблицы сложных процентов, получим:
откуда х = 4 дня. 203. Прибыль торговой фирмы может составить для каждой партии товара: при закупке партий в 1000 единиц (100 - 80) х 1000 = 20 000 у. д. ед.; при закупке партий в 2000 единиц (100 - 60) х 2000 = 80 000 у. д. ед. Если фирма располагает информацией о том, что с равной вероятностью может иметь место спрос как на 1000, так и на 2000 единиц товара, то среднеожидаемая прибыль (математическое ожидание прибыли) равна:
20 000 х 0,5 + 80 000 х 0,5 = 50 000 у. д. ед.
Если такая полная информация о покупательском спросе отсутствует и будет принято решение о закупке 1000 единиц товара при вероятности реализации этой партии 0,5, то прибыль составит:
20 000 х 0,5 = 10 000 у. д. ед.,
а при закупке 2000 единиц (при той же вероятности реализации):
80 000 х 0,5 = 40 000 у. д. ед.
Следовательно, даже при более благоприятном варианте закупки 2000 единиц потери от неполноты информации равны:
50 000 - 40 000 = 10 000 у. д. ед.
1) Это и есть стоимость информации, т. е. та сумма, которую целесообразно израсходовать на изучение покупательского спроса. 2) Наиболее прибыльна закупка партии товара при наличии полной информации: в половине случаев следует закупать 1000 единиц товара, а в половине – 2000 единиц. 204. Обозначим вес большого арбуза через х, а стоимость одного килограмма его – через у. При этом стоимость большого и малого арбуза будет составлять:
Решая полученную систему из двух уравнений с двумя неизвестными, придем к квадратному уравнению:
Решая уравнение по стандартной формуле, получим:
x1 не подходит, так как общий вес покупки равен 14 кг. Следовательно, х2 = 10 – вес большого арбуза, а маленький арбуз весит 14-10 = 4 кг.
205. Обозначим капитал акционера А через х, а капитал акционера Б через у и составим два очевидных уравнения:
Решая совместно уравнения (1) и (2), найдем: х = 7 млн руб., у = 5 млн руб. 206. Проще всего решить эту задачу так. Мысленно включим в раздел еще один – восемнадцатый автомобиль. Тогда договорные доли от 18 автомобилей составят: для участника А – 9 автомобилей, для участника Б – 6 автомобилей, для участника В – 2 автомобиля. В сумме это и будет 17 автомобилей. Такой раздел не совсем точен, но понятен и по-своему справедлив. 207. Возраст фирмы Б равен: 31 -8 = 23 года. Возраст фирмы А : 23 х 2 = 46 лет. 208. Обозначив уставной фонд предприятия А через х, а уставной фонд предприятия Б через у, можем записать:
Из этого следует, что
Иными словами, уставной фонд предприятия Б в полтора раза больше, чем предприятия А. 209. Обозначив через х искомое количество акционеров, составим следующее очевидное уравнение:
Решение этого уравнения дает искомый ответ: х = 30 человек. 210. Вначале определим, какой процент от общего числа составляют отсутствующие акционеры:
Тогда процент, который составляли присутствующие акционеры, будет равен:
100 % - 16,7 % = 83,3 %. 211. Обозначим уставной фонд в рублях через х, тогда доля первого участника в уставном фонде составит
откуда следует, что х = 30 000 руб. Доля первого участника – 10 000 руб., доля второго – 7500 руб., доля третьего – 6000 руб. 212. Если обозначить время, которое прошло, через х, то оставшееся время будет равно
а всего в сутках
отсюда х = 8 часам (утра). 213. Обозначив возраст предприятия через х, можно записать условие задачи следующим образом: |
|

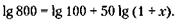
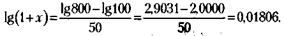

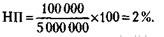
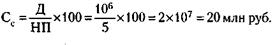
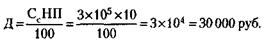
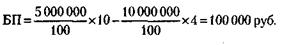

 , что составляет 30 %.
, что составляет 30 %. 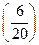
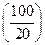 акций, то доход по ним составит 30 тыс. руб. (30 % от 100 тыс. руб.).
акций, то доход по ним составит 30 тыс. руб. (30 % от 100 тыс. руб.).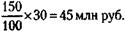
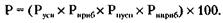
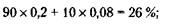
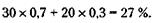

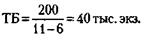
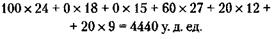
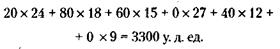

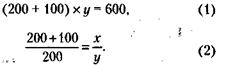
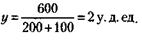
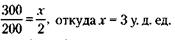
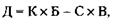

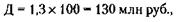
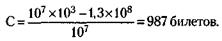
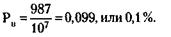
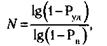
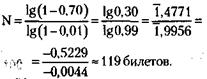

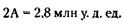
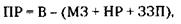
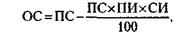
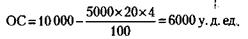
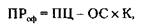
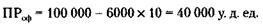

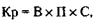

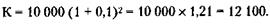
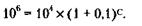
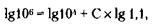
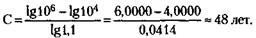
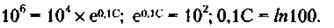
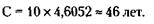
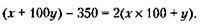
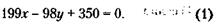
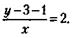

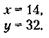
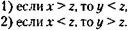
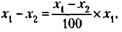
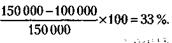
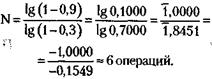

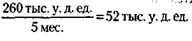

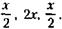
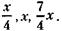
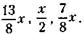
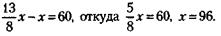
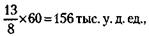
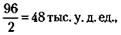
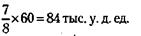

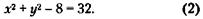
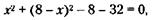
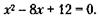
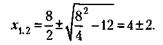
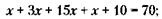

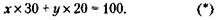
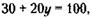
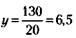
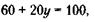
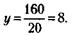
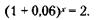
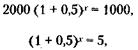
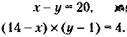
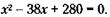
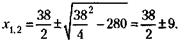
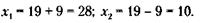
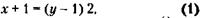


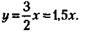
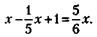
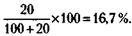
 х, доля второго участника -
х, доля второго участника -  , доля третьего -
, доля третьего -  х, а весь уставной фонд будет равен:
х, а весь уставной фонд будет равен: