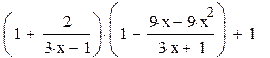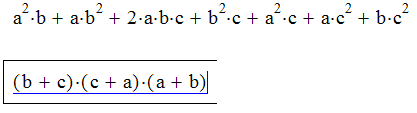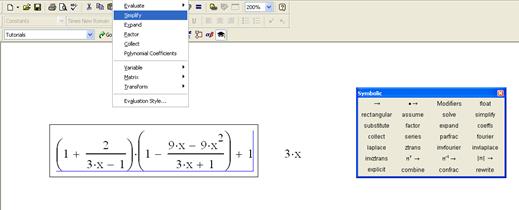
Тема 1. Символьные вычисления с использованием

встроенных операторов пакета MathCAD

Наряду с численным выводом, в MathCAD имеется возможность символьного, или аналитического, вычисления значения выражений. Для символьных вычислений имеется ряд специальных средств, которые будут детально рассмотрены позднее, самое простое из них – это оператор символьного вывода (Symbolic Evaluation). Он находится в меню Symbolic (рис. 1.2) и обозначается символом →.

Рисунок 1.2. Кнопка вставки оператора символьного вывода

В большинстве случаев этот оператор применяется так же, как оператор численного вывода, однако внутреннее различие между действием этих двух операторов огромно: численный вывод – это, в обычном смысле этого слова, «запрограммированный» расчет по формулам и численным методам, скрытый от глаза пользователя, а символьный вывод – результат работы системы искусственного интеллекта, встроенной в MathCAD, и называемой символьным процессором. Работа символьного процессора также невидима (и, чаще всего, даже трудно представима) пользователю и заключается в анализе самого текста математических выражений. Конечно, символьно можно рассчитать гораздо более узкий круг формул, так как относительно небольшая часть математических задач допускает аналитическое решение. Рассмотрим пример.

Пример: Вычислить символьно математическое выражение В•sin(arcsin(С•Х)), где В, С, Х – некоторые переменные.

Алгоритм решения задачи:

• Ввести выражение В•sin(asin(С•Х));

· Ввести оператор символьного вывода сочетанием клавиш <Ctrl+<>, либо нажатием соответствующей кнопки на панели Symbolic (Символика) или Evaluation (Выражения);

· Полученное решение появится cправа от символа оператора символьного вывода: В•sin(arcsin(С•Х))→B·C·x.

Если символьному процессору MathCAD не удается аналитически упростить выражение, то оно будет выдано справа от знака → в том же виде, что и слева. Для символьного вывода не требуется предварительно определять переменные, входящие в левую часть выражения! Если же переменным были все-таки присвоены ранее некоторые значения, символьный процессор просто подставит их в упрощенную формулу и выдаст результат с учетом этих значений.

В MathCAD можно выполнить следующие символьные преобразования алгебраических выражений:

simplify (упростить) – выполнить арифметические операции, привести подобные, сократить дроби, использовать для упрощения основные тождества (формулы сокращения, тригонометрические тождества и т.д.);

expand(развернуть) – раскрыть скобки, перемножить и привести подобные;

factor (разложить на множители) – представить, если это возможно, выражение в виде произведения простых сомножителей;

substitute (подставить) – заменить в алгебраическом выражении букву или выражение другим выражением;

convert to partial faction – разложить рациональную дробь на простейшие дроби.

Рассмотрим примеры, которые необходимо выполнить в задании №1. Задание выполняется каждым студентом самостоятельно. Задачи по теме 1, которые необходимо выполнить, находятся в таблицах 1.1 – 1.11. Номер варианта определяется по последней цифре номера зачётной книжки студента.

Задача 1. Упростить выражение с применением встроенного оператора Simplify:

Указание: Для начала необходимо ввести выражение в рабочее поле программы, используя клавиатуру:

<1> <+> <2> </> <3> <*> <x> <-> <1>

Прежде чем вводить знак умножения и второй сомножитель, нажмите несколько раз клавишу <пробел>, пока не выделится все введенное выражение линией, после чего нажмите на клавишу <*>. Первый сомножитель выделится скобками. После этого вводим второй сомножитель: <(> <1> <-> <9> <*> <x> <-> <9> <*> <x> <^> <2> <Space> несколько раз, пока не выделится 9x-9x²; </> <3> <*> <x> <+> <1> <Space> несколько раз, пока не выделится второй сомножитель <+> <1>.

Выделите введенное выражение, затем выбирайте на панели символьных вычислений (см. рис. 1.1) функцию Упростить (Simplify). Результат показан на рисунке 1.3.

Рисунок 1.3. Упрощение алгебраического выражения

Задача 2. Разложить по степеням выражение с применением встроенного оператора Expand.

Указание: Выделите введенное выражение, и затем выбирайте на панели символьных вычислений (см. рис. 1.1) функцию Расширить (Expand). Результат показан ниже.

Задача 3. Разложить на множители выражение с применением встроенного оператора Factor.

Указание: Выделите введенное выражение, затем выбирайте на панели символьных вычислений (см. рис. 1.1) функцию Фактор (Factor). Результат показан ниже.

Задача 4. Разложить выражение по подвыражению с использованием процедуры Collection Subexpression.

Указание: Для этого необходимо выбрать на панели символьных вычислений (см. рис. 1.1) функцию Подобные (Collect), слева ввести выражение, затем ввести переменную, по которой приводим подобные (в нашем случае - по х). Результат показан ниже.

Задача 5.Определить коэффициенты полинома, используя встроенную процедуру Coeffs.

Указание: Для этого необходимо выбрать на панели символьных вычислений (см. рис. 1.1) функцию Коэффициенты полинома (Coeffs), слева ввести выражение, затем ввести переменную, по которой приводим подобные (в нашем случае - по х). Результат показан ниже.

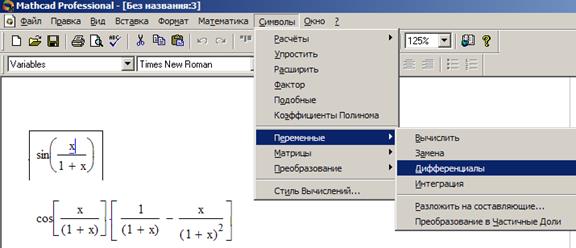
Задача 6.Продифференцировать выражение.

Указание: Для этого необходимо ввести выражение, и, выделив его, выбрать в меню Символы (Symbolic) функцию Переменные (Variable), далее Дифференциалы (Differentiate). Результат показан на рисунке 1.4.

Рисунок 1.4. Пример дифференцирования

Задача 7.Проинтегрировать выражение.

Указание: Для этого необходимо ввести выражение, и, выделив его, выбрать в меню Символы (Symbolic) функцию Переменные (Variable), далее Интеграция (Integrate). Результат показан ниже.

Задача 8.Произвести подстановку тождества f₁(x) в выражение y(x), применив оператор Substitute. Пусть известны выражение y(x) и тождество f₁(x).

Указание: Для этого необходимо в меню Символы (Symbolic) выбрать функцию Переменные (Variable), далее Замена (Substitute), слева ввести выражение y(x), затем ввести тождество f₁(x), по которому производим подстановку (в нашем случае – cos (x)²+sin (x)²═1). Обратите внимание на знак «═». Это, так называемое, Булево равенство. Оно находится в меню Вид →Панель инструментов →Булево →═. Результат показан ниже.

Задача 9.Разложить функцию f(x) в ряд Тейлора в окрестности точки x = 0 и взять первых девять членов ряда. Определить погрешность представления данной функции с помощью ряда для точки x = x₀. Пусть известны функция f(x) и величина x₀.

Указание: Для этого необходимо выбрать на панели символьных вычислений (см. рис. 1.1) функцию Series, слева ввести функцию y(x), затем ввести количество членов ряда. Нужно учесть, что при вводе количества членов ряда нужно использовать знак Булево равенство «═». Оно находится в меню Вид →Панель инструментов →Булево →═. Результат показан ниже.

Задача 10.Разложить выражение относительно переменной x на элементарные дроби, с применением процедуры Parfrac.

Указание: Для этого необходимо выбрать на панели символьных вычислений (см. рис. 1.1) функцию Parfrac, слева ввести выражение, затем ввести переменную, по которой производим разложение (в нашем случае - по х). Результат показан ниже.

Задача 11.Найти пределы функции.

Указание: Для этого необходимо выбрать на панели математического анализа(см. рис. 1.1) функцию Предел (Lim), далее указать пределы функции и ввести выражение. Результат показан ниже.

Тема 2. Матричная алгебра

Рассмотрим задачи, которые необходимо выполнить в задании №1. Работа выполняется каждым студентом самостоятельно. Задачи по теме 2, которые необходимо выполнить, находятся в таблицах 1.12 – 1.14. Номер варианта определяется по последней цифре номера зачётной книжки студента.

Задача 11.Транспонировать матрицу.

Указание: Для этого необходимо использовать панель матриц(см. рис. 1.1), далее ввести свой вариант задания для решения. Результат показан ниже.

Задача 12.Найти обратную матрицу от известной матрицы.

Указание: Для этого необходимо использовать панель матриц(см. рис. 1.1), далее ввести свой вариант задания для решения. Результат показан ниже.

Задача 13.Вычислить аналитически определитель матрицы. Получить численный ответ с применением оператора Substitute, при этом известны коэффициенты a, b и c

Указание: Для этого необходимо использовать панель матриц(см. рис. 1.1) и оператор Substitute (см. выше задание 8), далее ввести свой вариант задания для решения. Результат показан ниже.

Тема 3. Решение уравнений