|
|
Определение характеристик случайной величины для выборки большого объема.Факультет «Процессы и машины в агробизнесе» Кафедра «Эксплуатация машинно-тракторного парка и высокие технологии в растениеводстве» Левшин А.Г., Левшин А.А., Бутузов А.Е., Майстренко Н.А. «Планирование и организация эксперимента» Рабочая тетрадь Москва Издательство РГАУ-МСХА
Планирование и организация эксперимента: Рабочая тетрадь/ Составители Левшин А.Г., Левшин А.А., Бутузов А.Е., Майстренко Н.А.- М.: Изд-во РГАУ-МСХА, 2015.- 48 с.
В рабочей тетради представлен материал для лабораторно-практических занятий по дисциплине «Планирование и организация эксперимента». Рабочая тетрадь предназначена для самостоятельной работы студентов, обучающихся по программам магистратуры по направлениям: «Агроинженерия», «Стандартизация и метрология», «Управление качеством» и «Эксплуатация транспортно-технологических машин и комплексы». Отдельные задания могут быть рекомендованы бакалаврам. Будут полезны для повышения квалификации специалистов, занимающихся вопросами испытании сельскохозяйственной техники и аспирантам.
© Левшин А.Г., Левшин А.А., Бутузов А.Е., Майстренко Н.А. © РГАУ-МСХА им. К.А. Тимирязева; © Издательство РГАУ-МСХА;
Статистическая обработка одномерной выборки случайной величины
Цель и задачи.
Цель – изучить методику статистической обработки одномерной выборки случайной величины. Задачи – освоить основные понятия (случайная величина, выборка, характеристики случайной величины), методику формулировки и проверки статистических гипотез, изучить требования к выборке и методику проверки их соблюдения, научиться определять достоверные статистические характеристики случайной величины.
Задание.
Для сформированной на компьютере выборки объемом N=_25___ выполнить проверки соблюдения требований к достоверной (репрезентативной) выборке: 1) проверить наличие грубых ошибок в выборке; 2) проверить соблюдение требований о случайном характере выборки; 3) проверить соблюдения требований о достаточности выборки; 4) определить оценочные статистические характеристики случайной величины.
Выполнение расчетов.
1. Определяем оценочные характеристики случайной величины: - выборочное среднее
- выборочная дисперсия
- среднее квадратическое отклонение
2. Проверяем наличие и исключаем грубые ошибки. Проверяем, является ли Xmax грубой ошибкой, и рассмотрим порядок проверки статистических гипотез. 2.1. Формулируем основную и альтернативную статистические гипотезы: H0 :_____________________________________; H1 :_____________________________________. 2.2. Для проверки справедливости выдвинутых гипотез выбираем статистический критерий и находим его расчетное значение
Таблица 1.1. Исходные данные для расчета оценочных характеристик.
2.3. Находим критическое значение статистического критерия по таблице 1.2.
Таблица 1.2. Значения Uα; nкритерия V (для отбрасывания грубых ошибок при измерениях), определяемые из условия Р(V> Uα; n)=α
2.4. Расчетное значение критерия Vр сравниваем с критическим значением Vкр и выбираем справедливую гипотезу H0 или H1 . Вывод:_______________________________________________________________________________________________________________________ Проверяем, является ли Xmin грубой ошибкой. Расчетное значение критерия равно
Вывод: _______________________________________________________ ___________________________________________________________
3. Проверяем случайность выборки.
Для проверки случайности используем метод разностей. Для данной выборки формируем новую случайную величину di , равную разности смежных значений Рассчитываем дисперсию Cx 2
Проверку гипотезы о случайности выборки выполним по критерию τ
где Sx2 – дисперсия случайной величины X; Cx2 – дисперсия, подсчитанная по методу разностей.
Критическое значение выбранного критерия для объема выборки n ≤ 20
Таблица 1.3. Критические значения τα; kкритерия τ, определяемые из условия Р(τ< τα; k)=α
Для выборки объемом больше n>20 τ распределено по нормальному закону распределения с параметрами
В этом случае
Для n=25, α=0,05 находим параметр нормирования ЗНР Искомое значение будет равно Тогда
Если τр ≥ τкр , то принимаем гипотезу о случайности выборки, τр <τкр, то принимаем гипотезу о не случайном характере выборки. Вывод: ___________________________________________________________ __________________________________________________________________.
4. Оцениваем достаточность выборки.
1.Рассчитаем оценочное значение среднего (1.1) для первых 3, 5, 10 и 25 значений и построим график зависимости среднего от объема выборки
n Рис. 1.1 Зависимость среднего от объема выборки
Необходимо проанализировать закономерность изменения среднего Вывод: ____________________________________________________ _______________________________________________________________. 2.Определяем минимально необходимый объем выборки
Значение относительной погрешности задается методикой испытаний или измерений (в расчетах принимаем Δ=10% или 0,1). Полученное расчетное значение округляем до большего целого значения np =_________ и сравниваем с объемом выборки Вывод:______________________________________________________________________________________________________________________.
5. Определение минимально необходимого числа измерений при разработке методики исследования.
В практической работе исследователя чаще всего встречается задача обоснования необходимого числа измерений при разработке рабочей методики испытаний. На этом этапе выборочных значений не имеем. Значения величин по формуле (15) найти не можем, так как они зависят от искомого объема выборки. При выполнении задания необходимо самостоятельно разобраться и объяснить, как поступить в этом случае? Ответ студента: _______________________________________________ ______________________________________________________________________________________________________________________________________________________________________________________________________ Контрольные вопросы: 1. Дать определение случайной величины и привести примеры из своей практики. 2. Как будут изменяться статистические характеристики случайной величины при увеличении и выборки? 3. Объяснить порядок проверки статистических гипотез. 4. Объяснить понятие статистического критерия. 5. Как сравнить два исследуемых идентичных процесса с разными средними и дисперсиями одного признака?
Определение характеристик случайной величины для выборки большого объема.
Цель и задачи.
Цель – изучить методику статистической обработки выборки большого объема случайной величины. Задачи – освоить основные понятия (выборка большого объема, ряд распределения, гистограмма, полигон распределения, комулята), методику преобразования выборки в ряд распределения, научиться представлять в графическом виде ряд распределения, определять статистические характеристики случайной величины и оценивать их достоверность.
Задание Для анализа методики статистической обработки выборки большого объема необходимо определить по данным из 1-ого задания: - преобразовать выборку объемом n= 25 (взять из 1-ой работы) в ряд распределения; - определить статистические характеристики; - сравнить значения статистических характеристик, полученных в 1-ом и 2-ом задании.
2.3.Выполнение задания
1. Задаемся количеством классов m=_____ , на которые необходимо разбить интервал 2. Определяем ширину класса.
3. Строим расчетную таблицу. - установить левые и правые границы для каждого класса и занести в таблицу 2.1 ; - определить среднее значение для каждого класса Xi; - принимается допущение 1: «значение случайной величины может принимать любое значение в пределах интервала, но в расчетах используем среднее значение (установили вариационный признак); - подсчитываем количество выборочных значений, попадающих в каждый интервал (частоту) ni; - определяем частость (опытную вероятность) pi (проверить условие нормирования: - принимаем допущение 2: «значение вероятности в пределах интервала принимаем постоянными или подчиненными закону равномерной плотности».
Таблица 2.1 Расчетная таблица
4. Определяем статистические характеристики. Оценочное среднее:
Оценочная дисперсия:
5. Сравниваем полученные статистические характеристики, и характеристики подсчитанные в 1 задании.
Для сравнения статистических характеристик, полученных в 1-ой и 2-ой работе, подсчитаем относительную погрешность.
______________________________________ (2.3)
Для дисперсий:
Сравниваем полученные погрешности. Если относительная погрешность окажется более 5% указать возможные причины и какие возможные действия необходимо предпринять. ____________________________________________________________ ____________________________________________________________ ____________________________________________________________
Для приближения оценочной дисперсии
Для уменьшения относительной погрешности можно попробовать увеличить число интервалов и (или) провести дополнительные опыты.
6. Представить ряд распределения в графическом виде.
Для построения гистограммы на горизонтальной оси в выбранном масштабе отмечаем границы соответствующих интервалов. На вертикальной оси выбираем масштаб в соответствии с максимальным значением опытной вероятности и откладываем значения вероятности для интервала. Строят столбчатую диаграмму, затем середины столбчатой диаграммы соединяют отрезками ломаной прямой (рис. 2.1).
pi
X Рис.2.1 Гистограмма и полигон распределения
Для построения графика накопленных относительных частот по вертикальной оси в интервале (0,1) откладываем накопленные частоты из условия:
F*(x)
X Рис. 2.2 Опытная функция распределения (кумулята)
Контрольные вопросы: 1. В какой форме представлена случайная величина? 2. Какие причины могут вызвать большую относительную погрешность определения оценочной дисперсии? 3. Как будут изменяться частости (опытные вероятности) при увеличении числа измерений?
3. Выбор закона распределения случайной величины Цель и задачи
Цель – изучить методику выбора закона распределения для описания одномерной выборки случайной величины. Задачи – освоить основные понятия (закон распределения, функция распределения, функция плотности распределения, вероятность согласия), методику выбора закона распределения, изучить свойства функции распределения, научиться определять критические значения критериев согласия Пирсона и Колмогорова и вероятность согласия опытных данных определенному закону распределения.
3.2. Задание: Для имеющихся данных (задание 2) - проверить гипотезу о возможности использования закона нормального распределения для сглаживания опытных данных по критерию Пирсона (χ2); - проверить гипотезу о возможности использования закона нормального распределения для сглаживания опытных данных по критерию Колмогорова (l); - определить по одному из критериев вероятность согласия опытных данных и теоретической функции распределения с опытными параметрами.
Порядок выполнения
1.Проверка гипотезы по критерию согласия Пирсона.
- из таблицы 2.1 перенести значения середин интервалов Xi и опытные вероятности pi в таблицу 3.1(столбцы 2 и 3); - вычислить параметр нормирования ti для закона нормального распределения (среднее
- по значению ti находим по таблице 9 (приложение 1) значения теоретической функции плотности распределения для закона нормального распределения
Таблица 3.1. Расчетная таблица преобразования выборки в ряд распределения
- подсчитаем расчетное значение критерия Пирсона
- найдем критическое значение критерия Пирсона
- сравним полученное расчетное значение с критическим и сделаем вывод о справедливости проверяемой гипотезы: _______________________ __________________________________________________________ 2 Проверка гипотезы по критерию согласия Колмогорова А.Н.
- из таблицы 3.1 переносим значения середин интервалов xi, опытные вероятности pi и параметра нормирования ti ; - находим значения опытной функции F*(xi) распределения для середины интервалов (столбец 5): F*(x1)=1/2p1=____________; F*(x2)=p1+1/2p2=__________________; F*(x3)=p1+p2+1/2p3=________________________; F*(x4)=p1+p2+p3+1/2p4=___________________________; F*(x5)=p1+p2+p3+p4+1/2p5=______________________________; - находим значения теоретической функции распределения для ti по таблице 10 (приложение 1), при этом учитываем знак: для ti<0 значение F(x)=0.5-Ф(t), а для ti>0 значения F(x)=0.5+Ф(t). Полученные значения заносят в таблицу 3.2 (столбец 6); - находим разницу между опытной и теоретической функцией распределения (столбец 7):
- находим максимальное значение Di и рассчитываем расчетное значение критерия Колмогорова: Dmax =max
Таблица 3.2 Расчетная таблица для критерия Колмогорова
- по таблице 5 (приложение 1) находим критическое значение для заданного уровня доверительной вероятности 0,95 - сравниваем критическое значение с расчетным lр и делаем вывод о справедливости проверяемой гипотезы: ____________________________ _________________________________________________________________. Контрольные вопросы: 1. Что оценивает расчетное значение критерия Пирсона? 2. Что оценивает расчетное значение критерия Колмогорова? 3. С какой вероятность делается вывод о справедливости проверяемой гипотезы? 4. Как определить вероятность согласия опытных данных и теоретического закона распределения? 5. Как выбрать лучший закон распределения для имеющихся опытных данных?
|
|
 ; (1.1)
; (1.1) ; (1.2)
; (1.2) . (1.3)
. (1.3) . (1.4)
. (1.4)
 (1.5).
(1.5). = --------------- =________. (1.6)
= --------------- =________. (1.6)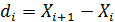 ( см. табл.1.1).
( см. табл.1.1). (1.7)
(1.7) , (1.8)
, (1.8)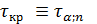 находим по таблице 1.3.
находим по таблице 1.3. ;
;  . (1.9)
. (1.9) определяется из условия
определяется из условия . (1.10)
. (1.10) по таблице 10 (приложения1) соответствующий уровню доверительной вероятности 0,95, получим
по таблице 10 (приложения1) соответствующий уровню доверительной вероятности 0,95, получим  , для 0,05
, для 0,05 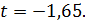
 . Значение
. Значение 
 подсчитываем по формуле (9)
подсчитываем по формуле (9) 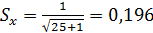
 (1.11)
(1.11)
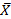
 при увеличении объема выборки.
при увеличении объема выборки. . (1.15)
. (1.15) .
. .
. );
);


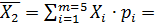 _________________________________________. (2.1)
_________________________________________. (2.1) ______________________________________._ (2.2)
______________________________________._ (2.2) Для средних значений:
Для средних значений: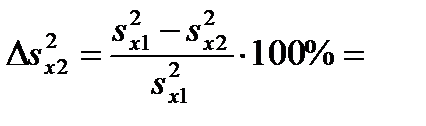 ______________________________________ (2.4)
______________________________________ (2.4)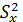 к истинному значению при ограниченном числе опытных данных вводят корректирующую поправку Шепарда.
к истинному значению при ограниченном числе опытных данных вводят корректирующую поправку Шепарда. =. (2.5)
=. (2.5) . По горизонтальной оси, как и для гистограммы, отмечаем границы интервалов.
. По горизонтальной оси, как и для гистограммы, отмечаем границы интервалов. =______ и среднее квадратическое
=______ и среднее квадратическое  берутся из задания 1). Значения ti записываем в столбец 4 таблицы 3.1.
берутся из задания 1). Значения ti записываем в столбец 4 таблицы 3.1.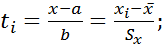 (3.1)
(3.1) ;
;
 ; (3.4)
; (3.4) , по таблице 4 (приложение 1) для уровня достоверности 0,95 и числу степеней свободы k=m-1=5-1=4
, по таблице 4 (приложение 1) для уровня достоверности 0,95 и числу степеней свободы k=m-1=5-1=4 ; (3.5)
; (3.5) ; (3.6)
; (3.6)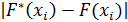 = _________; (3.7)
= _________; (3.7) ; (3.8)
; (3.8)