|
|
Поиск области экстремума функции методом крутого восхождения (спуска)
Цель и задачи
Цель – изучить методику планирования многофакторного эксперимента для поиска области расположения экстремума функции. Задачи – освоить основные понятия планирования многофакторного эксперимента по методу крутого спуска (восхождения), научиться планировать, проводить и обрабатывать результаты многофакторного эксперимента при поиске опытным путем экстремума функции.
Задание Для уровней варьирования 3-х факторов, принятые в задании 6, и уравнения регрессии (6.6) : - рассчитать допустимые смещения вдоль осей для движения вдоль вектора градиента и составить план эксперимента; - с помощью имитационной модели для условного 3-х факторного пространства проводить опыты, начиная с центра факторного пространства; - после каждого опыта провести анализ динамики изменения частного сечения неизвестной функции отклика и проводить опыты до достижения максимума.
8.3. Порядок выполнения задания
1. Задаемся уровнями варьирования факторов Таблица 8.1). При выполнении задания уровни варьирования перенесем из задания 6.
Таблица 8.1. Уровни варьирования действующих факторов
2. В качестве опорного решения берем результаты полного факторного эксперимента (задание 6). Уравнение регрессии, полученное при проведении полного факторного эксперимента
3. Построение расчетной таблицы и матрицы планирования (таблица 8.2). 3.1.В первую строчку запишем коэффициенты уравнения с соблюдением знака (учитываем только значимые значения коэффициентов). 3.2.Значения коэффициентов умножаем на величину интервала варьирования (табл.8.1) и результат записываем во вторую строчку. 3.3.Находим базовый коэффициент, соответствующий минимуму абсолютных значений второй строчки. 3.4.Подсчитываем масштабный коэффициент и рассчитываем расчетный шаг движения вдоль градиента (строчка 3). Расчетные значения округляют до удобного для реализации эксперимента значения Δi.
Таблица 8.2 Расчетная таблица матрица планирования эксперимента
4. Проведение имитационного моделирования. Задать начальную точку, соответствующую центру эксперимента (точка xio ). Проведение эксперимента осуществляется в том же порядке, что и задании 6. Результаты моделирования среднее [mean(y)] заносят в таблицу 8.2. и анализируем значения функции отклика. Если происходит увеличение функции, продолжаем движение вдоль градиента пока значения не начнут уменьшаться. В окрестности максимальной точки далее следует искать искомый максимум. Контрольные вопросы: 1. Как выбрать начальную точку планирования эксперимента? 2. Как определить направление движения в факторном пространстве? 3. Как определить шаг движения вдоль градиента? 4. При каком условии прекращается проведение эксперимента?
Описание области экстремума функции уравнениями второго порядка
Цель и задачи.
Цель – изучить методику планирования многофакторного эксперимента для описания области экстремума функции уравнениями второго порядка. Задачи – освоить основные понятия планирования многофакторного эксперимента для планов второго порядка, научиться планировать, проводить и обрабатывать результаты многофакторного эксперимента при описании области экстремума функции уравнениями второго порядка.
Задание. С помощью имитационной модели для условного 2-х факторного пространства: - выбрать диапазоны варьирования факторов для точки локального экстремума (координаты, полученные при выполнении задания 8); - построить план-матрицу планирования многофакторного эксперимента типа В2; - провести имитационное моделирование эксперимента в соответствии с блоком планирования план-матрицы и выбранными уровнями варьирования факторов; - провести дисперсионный анализ полученных результатов; - найти экстремум полученной функции отклика.
9.3. Порядок выполнения задания
1.Определить уровни варьирования факторов. При выборе уровней варьирования факторов в качестве основного уровня принять координаты локального экстремума, полученные при выполнении задания 8. Затем задаться интервалами варьирования факторов и рассчитать верхний и нижний уровни. Данные записать в таблицу 9.1. В дальнейшем принять один фактор постоянным и свести задачу к 2-х факторной (исследовать частное сечение отклика).
Таблица 9.1. Уровни варьирования действующих факторов
2.Построить план-матрицу эксперимента типа В2. Для этого по принципу центрального композиционного планирования в качестве ядра плана выбираем план ПФЭ 22 (4 опыта). В качестве звездных точек выбираем точки пересечения вписанной окружности в факторное пространство (количество точек 2n=4). Выделенные столбцы представляют блок планирования.
Таблица 9.2. План- матрица эксперимента В2
3.Проведение имитационного моделирования. Проведение имитационного эксперимента по программе «Планирование эксперимента» (рис. 6.1) осуществляется в том же порядке, что и в предыдущем задании 6. Результаты моделирования: среднее значение функции отклика
Рис. 9.1 Программа «В2Н» определения коэффициентов уравнения регрессии.
4.Дисперсионный анализ результатов эксперимента. 4.1. Проверка однородности ряда дисперсий
Критическое значения критерия равно
Расчетное значение сравниваем с критическим и делаем вывод: _________________________________________________________________ 4.2. Определяем дисперсию воспроизводимости
Число степеней свободы для дисперсии воспроизводимости 4.3. Определение коэффициентов уравнения регрессии. Значения коэффициентов уравнения регрессии находим по методу наименьших квадратов в матричной форме по программе «В2Н» (рис. 9.1). Для определения коэффициентов вводим в программу вектор полученных значений функции отклика Метод наименьших квадратов представлен в виде матричного уравнения
где x - матрица планирования (6х8). Получим уравнение
4.4. Определяем дисперсию адекватности
Число степеней свободы равно 4.5. Оцениваем адекватность модели. Для оценки адекватности полученного уравнения подсчитываем расчетное значение критерия Фишера
Критическое значение критерия находим по таблице 7 (приложения 1) для α=0.05;
Сравниваем расчетное значение с критическим и делаем вывод: ____ ______________________________________________________________ 5. Оцениваем значимость коэффициентов уравнения регрессии. Для этого определяем среднее квадратическое отклонение для коэффициентов
Далее определяем расчетные значения критерия Стьюдента для каждого коэффициента при неизвестных
По таблице 1 (приложения 1) определяем критическое значение критерия Стьюдента для α=0.05,
Сравниваем расчетные значения с критическим и делаем вывод: _____ _______________________________________________________________ 6. Находим экстремум функции отклика. Для уравнения 2х переменных
Находим решение системы уравнений: Полученные значения в кодированной системе координат переводим в физическую систему _________________________________________________________.
Контрольные вопросы: 1. По какому принципу формируется блок планирования план-матрицы? 2. На что влияет выбираемая величина интервала варьирования? 3. Как повысить точность определения коэффициентов уравнения регрессии ? 4. Какие виды планов второго порядка Вы знаете и опишите их особенности? Содержание
Учебное издание Составители: |
|
 . (8.1)
. (8.1)







 (9.1)
(9.1)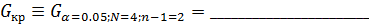 . (9.2)
. (9.2)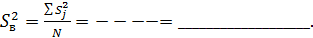 (9.3)
(9.3) равно
равно 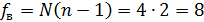 .
.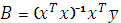 , (9.4)
, (9.4) . (9.5)
. (9.5)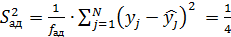 ________=__________ (9.6)
________=__________ (9.6)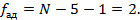
 =----------=_________________. (9.7)
=----------=_________________. (9.7)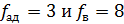
 . (9.8)
. (9.8) (9.9)
(9.9)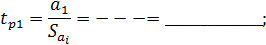
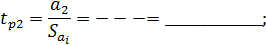
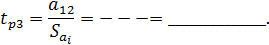


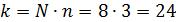
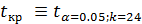 = ________.
= ________.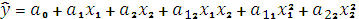 находим частные производные и приравниваем их к нулю:
находим частные производные и приравниваем их к нулю: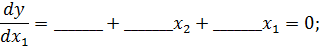
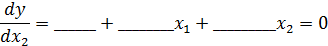
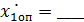 __;
__;