|
|
Оценка статистической взаимосвязиДвух случайных величин
Цель и задачи
Цель – изучить методику статистической оценки системы случайных величин. Задачи – освоить основные понятия (система случайных величин, эллипс рассеивания, ковариация и корреляционный момент, коэффициент парной и множественной корреляции), методику оценки статистической взаимосвязи двух случайных величин, изучить виды взаимосвязи случайных величин, научиться определять коэффициент парной корреляции и оценивать его значимость.
Задание
1.Для заданного типа сельскохозяйственных машин разных марок и производителей по справочным данным выбрать два показателя (4…6 значений) и оценить их взаимосвязь. 2. Оценить значимость взаимосвязи между выбранными параметрами однотипных машин. 3. Для области рассеивания опытных данных получить уравнение большой оси эллипса рассеивания и привести его к каноническому виду. 4. Выбрать масштаб осей и нанести опытные данные на координатное поле и в пределах поля рассеивания точек нарисовать полученное уравнение.
Порядок выполнения
1. Для заданного вида сельскохозяйственных машин разных марок и производителей по каталогам или рекламным проспектам выбрать два показателя и для 4…6 моделей однитипных машин занесем в таблицу 4.1
Таблица 4.1. Исходные данные для оценки статистической взаимосвязи двух случайных величин
2. Определим статистические характеристики:
3. Оценим значимость коэффициента парной корреляции. Для этого расчетное значение коэффициента парной корреляции сравним с критическим значением (таблица 4.2)
Сравниваем расчетное и критическое значение и делаем вывод: __________________________________________________________________Находим уравнение большой оси эллипса (4.3) рассеивания и строим график
y
x Рис. 4.1 Корреляционная зависимость ________________
Таблица 4.2. Критические значения коэффициента парной корреляции
Контрольные вопросы:
1. Какие могут быть виды вероятностной взаимосвязи между двумя случайными характеристиками? 2. Может ли оценить наличие значимой взаимосвязи коэффициент парной корреляции для нелинейных зависимостей? 3. Как будет изменяться коэффициент парной корреляции при увеличении объема выборки? 4. С какой достоверность принимается или отвергается гипотеза о наличии вероятностной (стохастической) взаимосвязи между двумя случайными величинами?
Аппроксимация опытных данных математическими зависимостями по методу наименьших квадратов
Цель и задачи
Цель – изучить методику аппроксимации опытных данных математическими зависимостями. Задачи – освоить основные понятия (аппроксимация, линеаризация, дисперсия адекватности, регрессия) и методику аппроксимации опытных данных математическими зависимостями и оценки их достоверности, изучить метод наименьших квадратов, научиться определять эмпирические коэффициенты и оценивать точность математических уравнений на основе дисперсионного анализа.
Задание
1.Для имеющихся данных однотипны сельскохозяйственных машин разных марок и производителей (исходные данные задания 4) найти коэффициенты уравнения и дисперсию адекватности для прямой. 2. Для тех же данных найти коэффициенты уравнения и дисперсию адекватности для параболы (компьютерная программа «Регрессия»). 3. Сравнить полученные дисперсии и сделать вывод о виде зависимости, рекомендуемой для аппроксимации опытных данных.
5.3. Порядок выполнения задания
1. Находим по методу наименьших квадратов коэффициенты a и b уравнения прямой
Для уравнения
Число степеней свободы 2.Эмпирические коэффициенты для уравнения параболы находим по программе «Полиноминальная регрессия» (рис. 5.1). Для этого в водим вектор переменной x и y (рис.5.1). В результате расчета в векторе S для уравнения 2-ой степени три последних цифры показывают значения коэффициентов уравнения: a=_______; b=________; c=________ и дисперсии адекватности
Рис. 5.1. Программа «Полиноминальная регрессия»
3. Сравниваем дисперсии
По таблице 7 (приложение 1) находим критическое значение
Вывод:_____________________________________________ ___________________________________________________ Контрольные вопросы: 1. В чем разница корреляционного и регрессионного уравнения? 2. В чем суть метода наименьших квадратов? 3. Если подобрать значения фактора так, что сумма будет равна нулю 4. Что оценивает дисперсия адекватности? 5. Как поступить, если расчетное значения критерия Фишера будет меньше 1? Планирование полного факторного эксперимента (ПФЭ) 2n.
Цель и задачи
Цель – изучить методику планирования многофакторного эксперимента для получения линейной формы. Задачи – освоить основные понятия планирования многофакторного эксперимента и методику дисперсионного анализа полученных результатов, метод наименьших квадратов для ортогональных матриц, научиться планировать и проводить многофакторный эксперимент и оценивать адекватность полиноминального уравнения и значимость его коэффициентов.
Задание С помощью имитационной модели для условного 3 факторного пространства: - задаться диапазоном варьирования каждого фактора; - построить план-матрицу полного факторного эксперимента (ПФЭ 23; - провести имитационное моделирование в соответствии с блоком планирования план-матрицы и выбранными уровнями варьирования; - провести дисперсионный анализ полученных результатов; - получить уравнение регрессии и оценить его адекватность; - оценить значимость коэффициентов уравнения.
6.3. Порядок выполнения задания
1. Выбираем уровни варьирования действующих факторов. Верхний и нижний уровень варьирования каждого действующего фактора задаемся произвольно из допустимого диапазона (0,100) для условной физической системы и записываем в таблицу 6.1. При выборе интервала варьирования необходимо учитывать, что большие значения интервала повышают точность линейной аппроксимации, но при этом увеличивают погрешность описания.
Таблица 6.1. Уровни варьирования действующих факторов
2. Строим план-матрицу полного факторного эксперимента 23. План-матрица представляет таблицу (таблица 6.2), в которой в первом столбце указывается номер опыта (для плана 23 потребуется проведение 8 опытов), второй – фиктивный столбец, необходимый для определения среднего значения функции отклика, 3, 4 и 5 столбцы представляют блок планирования и указывают очередность одновременного изменения факторов. Для повышения точности аппроксимации включаем 3 повторности (столбцы 6, 7 и 8), в которые будем записывать результаты опытов. В столбцы 9 и 10 записываются результаты статистической обработки полученных результатов: среднее значение функции отклика в опыте и дисперсия. В последний столбец записывают значения отклика, подсчитанные по уравнению регрессии (6.6).
Таблица 6.2. План-матрица полного факторного эксперимента ПФЭ
3. Проведение имитационного моделирования. Проведение эксперимента осуществляется в следующем порядке. Для каждого опыта в соответствии с блоком планирования (столбцы переменных выделены жирной чертой) в программе «Планирование эксперимента» (МаthCAD, рис. 6.1) устанавливают значения переменных в физической системе (табл. 6.1) на верхнем (+1) или на нижнем (-1) уровне. В каждом опыте задают моделирование трех значений (n:=3) центрированных случайных поправок. Результаты моделирования заносят в таблицу 6.2 : - значения функции отклика для каждой повторности – 1, 2 и 3; - среднее [mean(y)] ; - дисперсию [var(y)]. В указанном порядке проводят 8 опытов.
Рис. 6.1. Программа имитационного моделирования «Планирование эксперимента»
4. Дисперсионный анализ результатов эксперимента 4.1. Проверяем однородность ряда дисперсий. Для оценки наличия грубых ошибок в полученных данных проверяем гипотезу об однородности ряда дисперсий, для этого выбираем максимальное значение дисперсии из проведенных опытов и подсчитываем расчетное значение критерия Кохрена
Критическое значения критерия находят по таблице 8 (приложение 1 Методических указаний) для относительной ошибки α=0,05, для N=8 опытов и 3 повторностей n=3
Расчетное значение сравнивают с критическим и делают вывод: _________________________________________________________________ _________________________________________________________________ 4.2. Определяем дисперсию воспроизводимости, оценивающую точность определения показателя (отклика функции) y
Число степеней свободы для дисперсии воспроизводимости 4.3. Определяем коэффициенты
Для ортогональной матрицы (
Получим уравнение
4.4. Определяем дисперсию адекватности
Число степеней свободы для дисперсии адекватности равно 4.5. Оцениваем адекватность полученного уравнения, для чего сравниваем дисперсию воспроизводимости
Критическое значение критерия находим по таблице 7 (приложения 1 Методических указаний) для α=0.05;
Сравниваем расчетное значение с критическим и делаем вывод: ____ ______________________________________________________________ ______________________________________________________________ 4.6. Оцениваем значимость коэффициентов уравнения регрессии. Для этого определяем среднее квадратическое отклонение для коэффициентов
Далее определяем расчетные значения критерия Стьюдента для каждого коэффициента при неизвестных
По таблице 1 (приложения 1 Методических указаний) определяем критическое значение критерия Стьюдента для α=0.05,
Сравниваем расчетные значения с критическим и делаем вывод: _____ _______________________________________________________________ _______________________________________________________________
Контрольные вопросы: 1. Что собой представляет нормированное факторное пространство? 2. Как подсчитать значения отклика y для заданной точки факторного пространства: 3. Можно ли по значениям оценить силу влияния каждого фактора?
Планирование дробного факторного эксперимента (ДФЭ) 2n-k
Цель и задачи
Цель – изучить методику планирования дробного многофакторного эксперимента для получения линейной формы уравнения. Задачи – освоить основные понятия планирования дробного многофакторного эксперимента, научиться планировать, проводить и обрабатывать результаты многофакторного эксперимента и оценивать адекватность уравнения.
Задание С помощью имитационной модели для условного 3-х факторного пространства для диапазонов варьирования факторов, принятых при моделировании полного факторного эксперимента (задание 6): - построить план-матрицу дробного факторного эксперимента ДФЭ 23-1; - провести имитационное моделирование в соответствии с блоком планирования план-матрицы и заданными уровнями варьирования; - провести дисперсионный анализ полученных результатов; - получить уравнение регрессии и оценить его адекватность.
7.3. Порядок выполнения задания
1. Задаемся уровнями варьирования факторов. В данном задании уровни варьирования перенесем из задания 6.
Таблица 7.1. Уровни варьирования действующих факторов
2. Построение план-матрицы дробного факторного эксперимента 23-1. За основу плана берем план-матрицу ПФЭ 22 (4 опыта). Значения фактора X3 приравняем к парному произведению
Таблица 7.2 План-матрица ДФЭ 23-1
3. Проведение имитационного моделирования. Проведение эксперимента осуществляется в том же порядке, что и в предыдущем задании 6. Результаты имитационного моделирования заносят в таблицу 7.2 : - среднее [mean(y)] ; - дисперсию [var(y)].
4. Дисперсионный анализ результатов эксперимента 4.1. Проверка однородности ряда дисперсий
Критическое значения критерия равно
Расчетное значение сравнивают с критическим и делают вывод: _________________________________________________________________ _________________________________________________________________ __________________________________________________________________ 4.2. Определяют дисперсию воспроизводимости
Число степеней свободы для дисперсии воспроизводимости 4.3. Определяют коэффициенты
Получим уравнение
4.4. Определяем дисперсию адекватности
Число степеней свободы равно 4.5. Для оценки адекватности полученного уравнения подсчитываем расчетное значение критерия Фишера
Критическое значение критерия находим по таблице (приложения 1) для α=0.05;
Сравниваем расчетное значение с критическим и делаем вывод: ____ ______________________________________________________________ ______________________________________________________________ _______________________________________________________________ Контрольные вопросы: 1. По какому принципу формируется блок планирования? 2. Что оцениваю коэффициенты уравнения? 3. Можно ли по значение коэффициентов однозначно утверждать о силе влияния того или иного фактора ? 4. Какое преимущество и недостатки имеет метод дробного планирования?
|
|
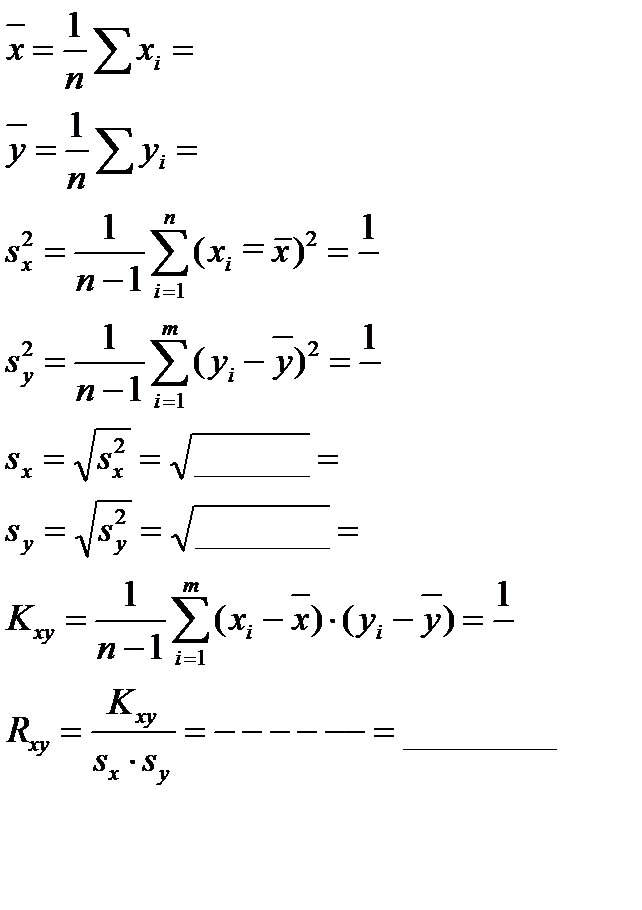
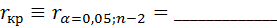 .
.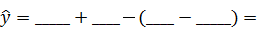 _____________.
_____________.
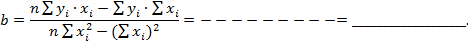
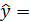 a
a 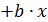 =_____+____x подсчитаем дисперсию адекватности
=_____+____x подсчитаем дисперсию адекватности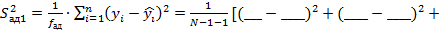
 ______________.
______________.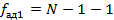 =_________.
=_________.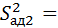 _______, Число степеней свободы
_______, Число степеней свободы 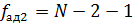 =______.
=______.


















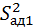 и
и  по критерию Фишера
по критерию Фишера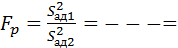 _______.
_______.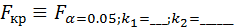 =__________.
=__________.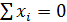 , как изменятся формулы для определения коэффициентов?
, как изменятся формулы для определения коэффициентов?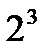
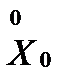
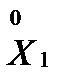

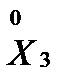
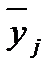












 (6.3)
(6.3)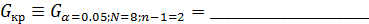 . (6.4)
. (6.4)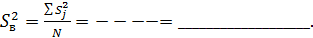 (6.5)
(6.5) равно
равно 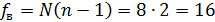 .
.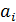 уравнения регрессии (6.6) по методу наименьших квадратов
уравнения регрессии (6.6) по методу наименьших квадратов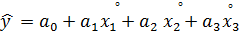 . (6.6)
. (6.6) метод наименьших квадратов примет вид
метод наименьших квадратов примет вид (6.7)
(6.7) .
.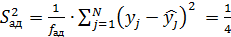 ________=__________ (6.8)
________=__________ (6.8)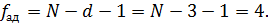
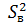 и дисперсию адекватности
и дисперсию адекватности 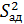 . Для этого подсчитываем расчетное значение критерия Фишера
. Для этого подсчитываем расчетное значение критерия Фишера =----------=_________________. (6.9)
=----------=_________________. (6.9)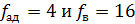
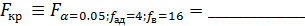 . (6.10)
. (6.10) (6.11)
(6.11)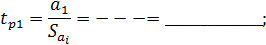
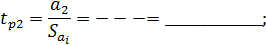

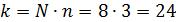
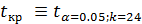 =__________.
=__________. ,
,  и
и 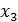 ?
?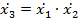 (столбец 5). Повторности будем учитывать при проведении имитационного моделирования, но в таблицу 7.2 будем записывать только средние значения и дисперсию.
(столбец 5). Повторности будем учитывать при проведении имитационного моделирования, но в таблицу 7.2 будем записывать только средние значения и дисперсию.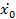
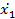
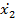
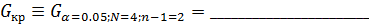 . (7.2)
. (7.2)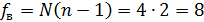 .
. ____-____+____-_____+_____)=______;
____-____+____-_____+_____)=______;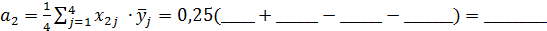 .
.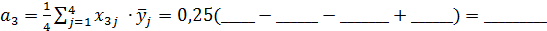 .
.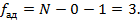 Если дисперсия адекватности близка к 0, точки принадлежат поверхности и п 7 не проводят, считаем модель адекватной.
Если дисперсия адекватности близка к 0, точки принадлежат поверхности и п 7 не проводят, считаем модель адекватной.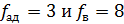
 . (7.9)
. (7.9)