|
|
Определение нормальной глубины для русла трапецеидальной формы сеченияВведение Существующие методики гидравлических расчетов по теме «Неравномерное движение воды в открытых руслах» [1,2,3], ориентированные на использование табличных данных и калькуляторов, для студентов весьма сложны, трудоемки и отнимают у них массу времени на выполнение лишних или точнее дополнительных действий, таких, например, как интерполяция по таблицам, вычерчивание таблиц и построение графиков. Для облегчения работы студентов и повышения производительности труда предлагается использовать современную систему компьютерной математики Mathcad. За основу принята методика, применяемая на кафедре «Гидравлика и водоснабжение» МИИТа [1,2]. Однако, непосредственное использование этой методики с применением специальных таблиц не представляется возможным. Между тем, разработанная нами программа в системе Mathcad позволила создать шаблоны расчетов, в которых студенту предлагается заменить исходные данные на свои, а с результатами по ходу расчетов студент может соглашаться или не соглашаться. В Приложениях 1,2 приведены два бланка заданий: «Задание 2, Вариант 1» и «Задание 2, Вариант 2». В дальнейшем мы будем называть их Задание 2/1 и Задание 2/2. Методика автоматизированного расчета Исходные данные Исходные данные для расчетов в данной работе используются из применяющихся до последнего времени бланков заданий [3]. Однако, ввод исходных данных в программу требует некоторых разъяснений. Часть исходных данных задается в задании непосредственно. К ним относятся: число N, коэффициент откоса – m, уклон дна канала – I0 и другие. Другая часть данных задана в виде зависимостей от N, например, расход воды Q и другие. В этих зависимостях вместо знака равенство необходимо ввести знак присвоения, набрав на клавиатуре «Shift+». Третья часть данных задается студентом по своему усмотрению, например глубина воды h. Эта часть исходных данных может быть введена в программу различными способами, от которых будут зависеть дальнейшие действия. В данной работе мы приводим несколько способов введения в документ-шаблон исходных данных. Перед началом работы необходимо запустить систему Mathcad. Помните, что ввод исходных данных и расчеты производятся на английском языке. Так, например, для Задания 2/1 исходные данные записываются следующим образом:
Значение
Расход воды Q: = 4 + 0.2·N Q = 12 м³/с
Ускорение свободного падения, м/с² g: = 9.81
Характеристики канала:
Коэффициент откоса
Относительная ширина канала
Ширина канала по дну b(h) := β·h
Уклон дна канала
Мощение дна и стенок канала – рваным камнем
Длина участка канала ГД, м
Глубина в конце участка канала ГД hд: = 2+0.01·N; hд=2.4 м Перепад БВГ: сечение на перепаде – прямоугольное; высота перепада P: = 2 + 0.02·N P = 2.8 м; ширина перепада должна быть такой, чтобы на участке АБ обеспечивалось равномерное движение. Результаты со знаком присвоения необходимо ввести заново, согласуясь с исходными данными своего варианта задания. Для удобства пользователя блоки присвоения, которые необходимо редактировать, выделены серым цветом и заключены в рамку. Блоки присвоения, содержащие массив, просто заключены в рамку. Блоки с формулами расчета отдельных показателей никак не выделены в тексте. После ввода своих исходных данных произойдет автоматический пересчет результатов. Блоки с выводом основных результатов вычислений выделены серым цветом.
Определение нормальной глубины для русла трапецеидальной формы сечения Данная задача по гидравлическому расчету каналов относится к типу задач, когда живое сечение канала не задано, т.е. не известны ширина и глубина канала, и их надо найти. Решаем задачу с двумя неизвестными [4].
Зададимся глубиной м. В этой рамочке после буквы h следует знак присвоения, первая цифра массива соответствует минимальному, а последняя – максимальному значению глубины h, вторая – является вторым числом массива, а разность между вторым и первым числами соответствует интервалу между числами множества h. Площадь живого сечения водного потока ω, смоченый периметр χ, гидравлический радиус R, коэффициент Шези C и расходная характеристика K определяются по известным формулам [4], но записываться должны, как функции от h.
h= ω(h) = χ(h) = R(h) = C(h) = K(h) = b(h) =

Определим значение заданной расходной характеристики K0 по формуле
Первый способ определения h0 - интерполяцией табличных данных. Определим по таблице значения K1 (ближайшее меньшее) и K2 (ближайшее большее по отношению к K0) и соответствующие им значения h1 и h2. Если наибольшее табличное значение K оказалось меньше значения K0, то интервал исходных (задаваемых) значений h необходимо сместить в сторону возрастания значений h. Если же наименьшее табличное значение K больше K0, то интервал исходных значений h следует сместить, наоборот - в сторону уменьшения значений h.
h1 : =1.6 h2 : =1.7 K1: =554.296 K2 : =651.273
h0 = 1.647 м Второй способ определения h0 – графо-аналитический. Используя данные таблицы, строим график K=f(h). Курсор совмещаем с пиктограммой «Инструменты графика» и кликаем левой клавишей мыши (КЛК). Появляются новые пиктограммы, из которых необходимо выбрать пиктограмму «Декартов график», КЛК, предварительно указав место расположения графика. Появится двойная рамка с метками в виде черного и красного квадратиков, в которых необходимо набрать с помощью клавиатуры название осей: по оси абсцисс – K(h), по оси ординат – h. КЛК вне рамки, появится график. Курсор совместить с графиком и произвести двойной клик левой клавишей мыши. Появится окно, в котором нужно убрать флажки (галочки) «Авто сетка» и указать число делений по осям. Установить флажки «Вспомогательные линии». Курсор совместить с «ОК» и КЛК. На графике появится сетка. Также флажки должны стоять в окнах «Нумерация». Для наглядности курсор наводим на графики, производим двойной КЛК. Появится меню, в котором необходимо активизировать (установить флажок) кнопки по осям X и Y «Показать метки», курсор совместить с «ОК» и КЛК. Возле каждой оси появятся по два черных маленьких прямоугольника. Совмещаем курсор с одним из них по оси X, КЛК, на клавиатуре набираем значение K0, курсор совмещаем с прямоугольником у оси Y, КЛК, и, определив по графику, набираем значение h0. Переводим курсор за пределы графика и КЛК, появятся перекрещивающиеся штриховые линии, возле которых будут указаны значения K0 и h0. Помните, что при изменении исходных данных, старый график надо удалить, КЛК на графике, курсор совместить с пиктограммой «Вырезать» и КЛК. Затем повторить все действия по построению графика.
Рисунок 1
Проверка правильности решения: Рассмотренные способы решения – не очень точные. Поэтому далее правомерность нашего решения необходимо проверить. Определяем расход Q0 при найденной глубине h0 и сравниваем с заданным значением расхода Q (см. прил. 1,2). Допускаемая ошибка в определении h0 не должна превышать 5% [1].
h0 = 1.647 b(h0) = 4.941
ω(h0) = 12.209 χ(h0) = 10.88 R(h0) = 1.122 C(h0) = 46.301 K(h0) = 598.789
Условие выполняется, принимаем для дальнейшего расчета
и . Условие не выполняется тогда, когда решение производилось грубо, т.е. слишком приближенно. В этом случае для уменьшения ошибки расчета нужно выбрать меньший шаг, задаваясь глубиной h, и, может быть, дополнительно увеличить число делений по осям при построении графика, если использовался второй способ расчета. |
|
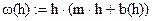

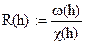
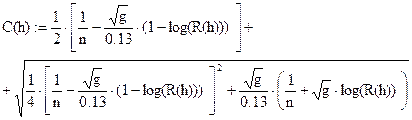
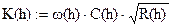































 K0 = 600 м³/c.
K0 = 600 м³/c.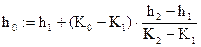
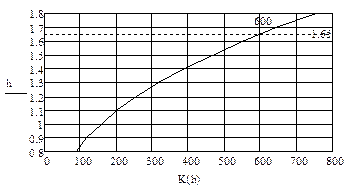
 Q0 = 11.976 ΔQ: = |Q-Q0| ΔQ = 0.024
Q0 = 11.976 ΔQ: = |Q-Q0| ΔQ = 0.024 δ = 0.202% δдоп ≤ 5 %
δ = 0.202% δдоп ≤ 5 %