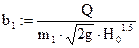|
|
Расчет кривой свободной поверхности потокаКривая свободной поверхности должна быть рассчитана для того участка канала, на котором имеет место неравномерное движение водного потока. В Задании 2/2 неравномерное движение будет на подводящем участке АБ, а на отводящем участке канала ДЕ будет равномерное движение. В Задании 2/1 на подводящем участке канала АБ будет равномерное движение, а на отводящем ГД – неравномерное. До расчета кривой свободной поверхности необходимо определить ее вид (кривая подпора или кривая спада). Для этого нужно сравнить друг с другом нормальную глубину h0, заданную глубину hд (Задание 2/1) или H (Задание 2/2) и критическую глубину hк [1].
Если hк<h0<hд(H) - кривая подпора; если hк<hд(H)<h0 – кривая спада; если hд(H)<hк<h0 – кривая спада с hк в сечении Д.
Определим вид кривой для нашего случая:
hк=0.826; h0=1.647; hд=2.4, т.е. имеет место кривая подпора 0.826<1.647<2.4.
Далее приступаем непосредственно к расчету кривой свободной поверхности потока. Для этого весь канал с неравномерным движением воды делится сечениями с глубинами h1 и h2 на несколько участков,
h2 - глубина в сечении ниже Длины этих участков определяют с помощью уравнения Б.А. Бахметева [4]. Начинают расчет с определения гидравлического показателя русла х. Он принимается постоянным для всего участка канала с неравномерным движением [1].
hср = 2.023 ωср = 16.14 χср = 12.237 Rср = 1.319
Гидравлический показатель русла
Принимаем α: = 1.2 . hд = 2.4 h0 =1.647 Разбивку канала на участки следует начинать от известной глубины hд (Задание 2/1) или H (Задание 2/2). Глубины в соседних сечениях должны отличаться друг от друга не больше, чем на 5…10 см [1]. Глубина русла на участке канала ГД (АБ – Задание 2/2) изменяется от hд=2.4 (Н-Задание 2/2) до h0=1.647 м, поэтому максимальное значение h2=2.4 м, а h1=2.3 м, минимальное значение h1=1.7 м (чуть больше значения h0), минимальное значение h2 больше h1 на 0.1 м, а hс=0.5(h1+h2)м.
Относительная глубина потока выше (η1) и ниже (η2) по течению:
Далее находят средние на рассматриваемом участке потока характеристики: ω(hс):=(b+m·hс)·hс
h1= h2 = hc = η1(h1)= η2(h2)= B(hc) =
ω(hc) = χ(hc) = R(hc) = C(hc) = K(hc) = j(hc) =
Расчет кривой свободной поверхности ведем по формуле Б.А. Бахметева, в которой вместо разности функций относительной глубины, определяемых по специальным таблицам [1], подставлен определенный интеграл. Границами этого интеграла являются относительные глубины η1(h1) и η2(h2), которые являются функциями h1 и h2, что не дает возможности определить значения интеграла. Поэтому, ранее определенные значения η1(h1) и η2(h2), необходимо переписать без знака функции, т.е η1 и η2. А чтобы можно было получить значения интеграла во всех сечениях и в дальнейшем перемножать и складывать с другими множествами, необходимо выражение интеграла справа от знака присвоения отметить синим уголком, пользуясь курсором и клавишей пробела, а затем векторизовать, совместив курсор (стрелочку) со знаком «Задать вектор» в окне «Матрицы» и КЛК.
Значения относительных глубин в виде векторов можно записать используя ниже приведенные формулы. Значение i должно соответствовать числу строк выше приведенной таблицы, за вычетом единицы i:=0.. 6 .
Далее курсором указывается место расположения этих векторов. В окне «Греческий алфавит» выбираем букву η, КЛК, с помощью клавиатуры набираем нужную цифру и знак равенства.
Для набора интеграла курсор совмещаем с кнопкой «Операторы математического анализа» на панели инструментов Math (Математика), КЛК, появляется окно, в котором курсор совмещаем со знаком определенного интеграла, КЛК, предварительно указав место его расположения. При помощи символов греческого алфавита и кнопок клавиатуры записываем границы и выражение под знаком интеграла. Совмещаем курсор с пиктограммой «Векторные и матричные операции», КЛК, появляется окно «Матрицы». В этом окне курсор совмещаем с кнопкой «Задать вектор» и КЛК, предварительно объединив интеграл справа от знака присвоения синим уголком с помощью клавиши «Пробел».
i: = 0.. 6
I:=
1-j(hc) =
 
Чтобы получить значение вектора V1, необходимо векторизовать произведение (V·І) по аналогии с интегралом. После этих преобразований формула для определения расстояний между соседними сечениями водного потока ΔL с глубинами, отличающимися друг от друга на 0.1 м (0.05 м), примет новый вид
Теперь необходимо записать вектор L1, каждый член которого представляет собой сумму предыдущих членов вектора ΔL. Для записи вектора L курсор совмещаем с кнопкой «Векторные и матричные операции» на панели Math, КЛК, появляется окно «Матрицы». Курсор совмещаем с кнопкой «Создать матрицу или вектор», КЛК. Появляется окно «Вставить матрицу», в котором необходимо указать число строк и столбцов, КЛК на клавише «ОК», предварительно указав место расположения вектора.
Запишем вектор L1 как вектор L, добавив ноль и округлив
i:=0…7 hi:=hд-0.1·i
Для построения кривой свободной поверхности воды в русле канала воспользуемся линейной регрессией общего вида. Если Вас значение i не устраивают, то Вы можете их изменить. Построение графика кривой производится аналогично предыдущему графику. Однако, возле оси Y через запятую записываются три функции: I0·L+h; I0·L; h0+I0·L. Набираем следующие функции, определяющие значения ординат. После каждой функции набираем знак равенства. Появляются три вектора.
Чтобы построить график нескольких функций, надо в черном прямоугольнике по оси абсцисс набрать букву L, а по оси ординат через запятую: I0·L+h, I0·L, h0+I0·L и КЛК.
Рисунок 3 Чтобы показать на чертеже отметку 2000 м, соответствующую заданной длине канала L (см. прил. 1), надо курсор совместить с графиком, КЛК два раза, появится окно, в котором необходимо активизировать кнопку «Показать метки» и КЛК на кнопке «ОК». У оси абсцисс вместо черного прямоугольника набрать на клавиатуре число 2000, против которого на графике появится вертикальная штриховая линия. Подобную операцию выполняют только для Задания 2/1, в котором необходимо определить глубину hг. Для определения глубины hг на расстоянии 2000 м от сечения Д – в сечении Г, составим пропорцию. Для определения параметров пропорции из значений векторов L и h выписываем L1 = 1497 (ближайшее меньшее от 2000 м) и соответствующее ему h1 = 2.0, а также L2=2007 (ближайшее большее к 2000 м) и h2 =1.9.
h1 : =2.0 h2 : =1.9 L1: =1497 L2 : =2007 Lг:= 2000
h1 – h2 = 0.1 L2 – L1 = 510 h1 – hг Lг – L1 = 503
h г = 1.901 м
Определение ширины перепада Ширину перепада необходимо определить только в Задании 2/1, т.к. в этом случае она неизвестна. В Задании 2/2 ширина перепада соответствует ширине отверстия дорожной трубы, расположенной на нем. Определяют ширину перепада b1 исходя из того, что в подводящем канале АБ движение равномерное с глубиной h0. Входная часть перепада по характеру работы близка к неподтопленному водосливу с широким порогом. Поэтому расчет ведется с использованием формулы пропускной способности такого водослива [4]
H0 – напор на водосливе; m1 – коэффициент расхода водослива.
Принимаем [1].
Средняя скорость в трапецеидальном канале при глубине h0
b1 = 3.684 м
|
|
 h1 - глубина в сечении выше по течению.
h1 - глубина в сечении выше по течению. ωср:=(b+m·hср)·hср
ωср:=(b+m·hср)·hср
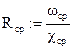
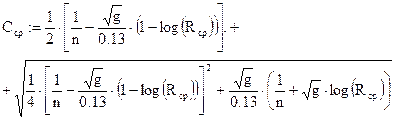
 Cср = 47.503 Kср = 880.525
Cср = 47.503 Kср = 880.525 x = 3.726.
x = 3.726. α = 1.216
α = 1.216
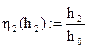
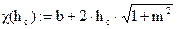
 B(hс):=2·m·hс+b
B(hс):=2·m·hс+b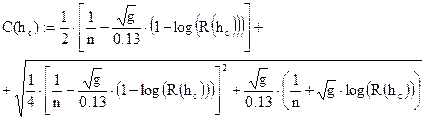
 ;
; 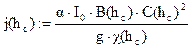










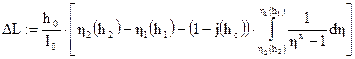

 η:=η2-η1
η:=η2-η1

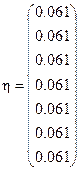

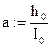




 ΔL:= а·(η –V1)
ΔL:= а·(η –V1) 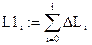

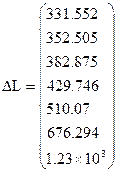
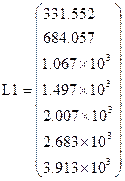


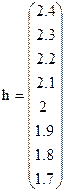


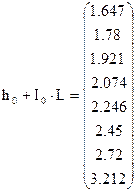
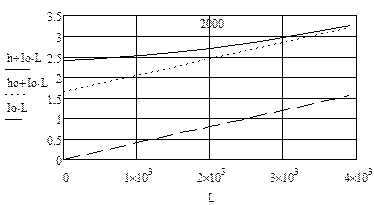
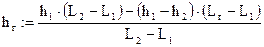
 , откуда находят b1.
, откуда находят b1.

 =0.983 м/с
=0.983 м/с H0 = 1.706 м
H0 = 1.706 м