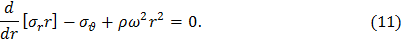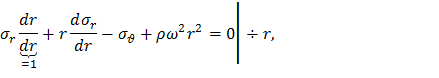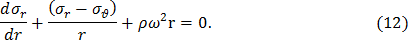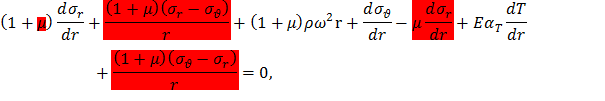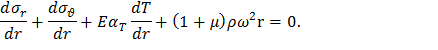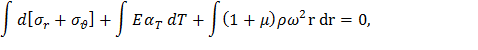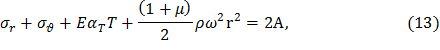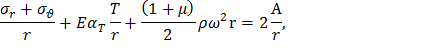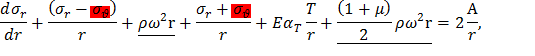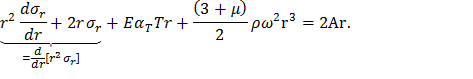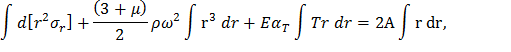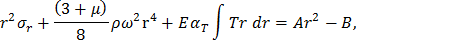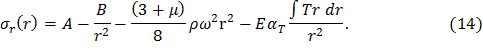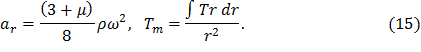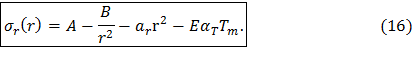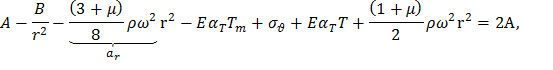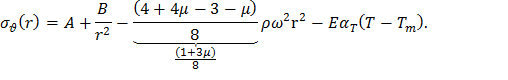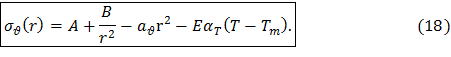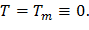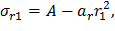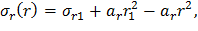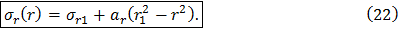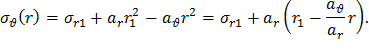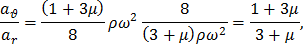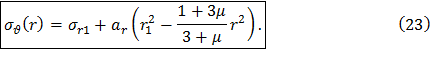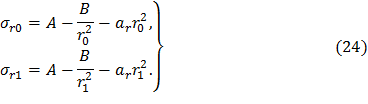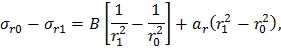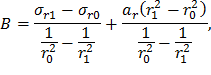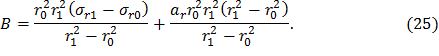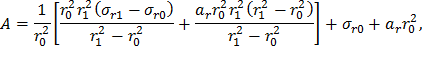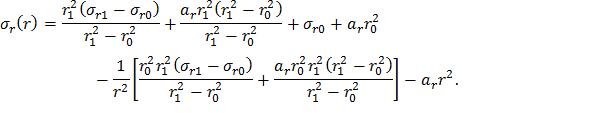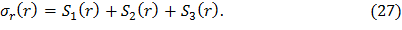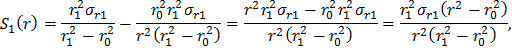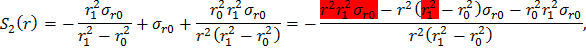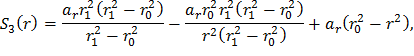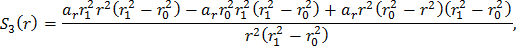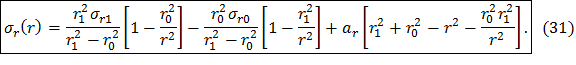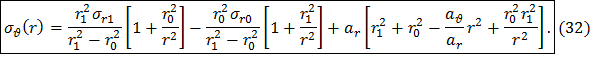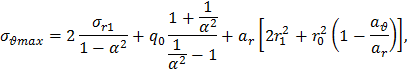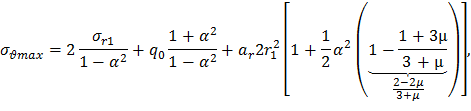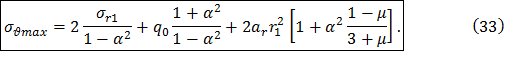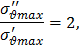Распределение напряжений в тонком вращающемся неравномерно нагретом диске постоянной толщины

Полагая h=const, из уравнения равновесия (4) получим

Применяя правило дифференцирования произведения, имеем

Уравнение равновесия (12) для диска постоянной толщины используем для исключения четвертого слагаемого в уравнении (9), что позволит легко его проинтегрировать. Для этого умножим (12) на 1+μ и сложим с (9):

В полученном уравнении разделим переменные и проинтегрируем, воспользовавшись правилом суммирования производных,

где 2A – постоянная интегрирования.

Уравнение равновесия в форме (12) содержит обе неизвестные величины σ_r и σ_θ. Исключим из него σ_θ, применив общее решение (13). С этой целью разделим (13) на r и сложим с (12):

В последнем уравнении разделим переменные и проинтегрируем

где B – постоянная интегрирования. Выразив из последнего соотношения σ_r, получим

Обозначим

Подставив введенные обозначения (15) в (14), окончательно получим общее решение для распределения радиальных напряжений в диске постоянной толщины:

Теперь из уравнения (13), учитывая (16), находим и σ_θ:

Обозначив,

окончательно получим общее решение для распределения окружных напряжений в диске постоянной толщины

Постоянные интегрирования A и B должны быть найдены из граничных условий (10) на периферии и расточке диска.

Вследствие линейности задачи полные напряжения в диске равны алгебраической сумме динамических и температурных напряжений, поэтому рассматривать их будем по отдельности.

Динамические напряжения в диске постоянной толщины
без центрального отверстия

Динамические напряжения определяются при следующих условиях:

Первое граничное условие из (19) означает, что в центре диска без центрального отверстия радиальное и окружное напряжения совпадают, из-за того, что исчезает различие между окружным и радиальным напряжениями.

Применим (19) к общим решениям (16) и (18). При r=0 имеем

Радиальные и окружные напряжения должны иметь конечные значения в центре диска при r=0, следовательно, параметр B равен нулю:

Подстановка второго граничного условия из (19) в общее решение (16) с учетом (20) даст

откуда можно выразить постоянную A:

Таким образом, распределение радиальных динамических напряжений в диске постоянной толщины без центрального отверстия получим из выражения (16), используя значения постоянных интегрирования в виде (20) и (21):

Распределение окружных динамических напряжений в диске постоянной толщины без центрального отверстия находится подстановкой (20) и (21) в общее решение (18):

Учитывая формулы (15) и (17) окончательно получим

На рис. 9 показаны эпюры динамических напряжений для сплошного диска постоянной толщины.

u eG1sUEsBAi0ACgAAAAAAAAAhAG6UR2K0JAAAtCQAABQAAAAAAAAAAAAAAAAAigsAAGRycy9tZWRp YS9pbWFnZTEucG5nUEsFBgAAAAAGAAYAfAEAAHAwAAAAAA== ">

Таким образом, максимальные значения радиальных и окружных динамических напряжений достигаются в центре диска.

Динамические напряжения в диске постоянной толщины
с центральным отверстием

Пусть T=T_m≡0, а радиальные напряжения на периферии и расточке диска соответствуют условиям (10). Подчиняя общее решение (16) этим условиям, получаем

Полученная система из двух алгебраических уравнений включает две неизвестных величины A и B. Для определения B вычтем из первого уравнение второе:

Выражение для A получим из первого уравнения системы (24), используя формулу (25):

Подставив соотношения (25) и (26) для параметров A и B в общее решение (16), получим

Сгруппируем слагаемые, содержащие σ_r1, σ_r0 и a_r, в комплексы S₁(r), S₂(r) и S₃(r) соответственно, а функцию σ_r(r) представим как

Подставив выражения (28), (29) и (30) в формулу (27), получим распределение радиальных динамических напряжений в диске постоянной толщины с центральным отверстием:

Распределение окружных динамических напряжений в диске постоянной толщины с центральным отверстием получим, выполнив подстановку соотношений (25) и (26) в общее решение (18):

Первые слагаемые в формулах (31) и (32) соответствуют напряжениям от периферийной нагрузки, вторые слагаемые соответствуют напряжениям от нагрузки на расточке диска, третьи слагаемые соответствуют напряжениям в свободно вращающемся диске без краевых нагрузок.

Типичные эпюры напряжений в диске с отверстием представлены на рис. 10. Очевидно, что максимальными будут окружные напряжения на расточке диска. Вычислим их, подставив значение r=r₀ в соотношение (32),

Обозначим α=r₀/r₁ и q₀=-σ_r. Тогда

При увеличении r₀ возрастает α и все три слагаемых в формуле (33), следовательно, растёт значение σ_θmax.

Сравним максимальное окружное напряжение σ^’’_θmax в диске с малым центральным отверстием при q₀ =0 с окружным напряжением σ^’_θmax в центре сплошного диска. При условии, что для малого отверстия α<<1 из формулы (33) имеем

Окружное напряжение в центре сплошного диска получаем из соотношения (23) при r=0:

Из уравнений (34) и (35) следует

то есть центральное отверстие малого диаметра в сплошном диске приводит к увеличению максимального окружного напряжения в 2 раза. Следовательно, малое отверстие в диске является источником концентрации напряжений с коэффициентом концентрации α_σ=2.