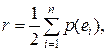Условные обозначения и диаграммы работы логических элементов

Реализуемая логическая функция	Условное обозначение	Диаграммы работы *
логическое НЕ
логическое И
логическое ИЛИ
исключающее ИЛИ
элемент И-НЕ
элемент ИЛИ-НЕ

В качестве базисных могут выступать элементы И-НЕ (функция Шеффера), а также ИЛИ-НЕ (функция Пирса). Их обозначения и диаграммы работы также приведены в таблице 9. Соответствующие таблицы истинности этих функций могут быть получены простым инвертированием значений функций И и ИЛИ.

Используя базовые элементы, можно построить все функциональные узлы ЭВМ. Например, основой ячейки памяти является триггер (от англ. trigger – защёлка) – устройство с двумя устойчивыми состояниями, устанавливающимися под воздействием внешних сигналов, что соответствует записи и хранению одного бита данных. Так называемый RS-триггер (от англ. reset – сброс и set – установка) может быть построен из двух элементов ИЛИ-НЕ, что показано в таблице 10. При подаче сигнала логической единицы на установочный вход S на выходе Q триггера также устанавливается единица, причём это состояние сохраняется и после снятия установочного сигнала. Подача сигнала логической единицы на вход сброса R устанавливает выход Q в ноль, который будет сохраняться до прихода единицы на вход S.

Таблица 10

RS-триггер

Условное обозначение	Схема реализации на элементах ИЛИ-НЕ	Диаграммы работы *

На основе триггера можно построить функциональные узлы, способные хранить n-разрядные двоичные числа (по одному триггеру на каждый бит), а также выполнять с ними некоторые специальные операции. Такие функциональные узлы называются регистрами. Существуют, например, регистры сдвига, осуществляющие сдвиг двоичного числа; регистры-счётчики, производящие подсчёт поступающих единичных сигналов.

Важнейшим устройством, выполняющим обработку информации в компьютере, является арифметико-логическое устройство (АЛУ). В основе АЛУ лежит устройство, реализующее арифметическую операцию сложения двух чисел – сумматор. Остальные арифметические операции реализуются с помощью представления чисел в дополнительном коде.

Элементы теории множеств

Множеством называется любое объединение определённых, вполне различимых объектов; их может и не быть вообще. Можно говорить о множестве точек на отрезке [0,1], множестве студентов в группе, множестве снежных дней в июле на экваторе, т.е. множество образуют любые объекты, объединённые по любому признаку. Объекты, составляющие множество, называются элементами множества. Множество, не имеющее ни одного элемента, называется пустым, обозначается Ø. Множество, состоящее из конечного числа элементов, называется конечным, в противном случае – бесконечным.

Задать множество можно перечислением его элементов. Например, множество, образованное из n элементов а₁, а₂, ..., а_n, обозначается А = {а₁, а₂, ..., а_n}; пишется а А (говорится «элемент а при надлежит множеству А»), если а является элементом множества А, в противном случае a A. Задать множество можно также, указав общее свойство для всех его и только его элементов. Например, множество равноудалённых от концов отрезка точек. Два множества считаются равными, если состоят из одних и тех же элементов; записывается А = В. Множество B называется подмножеством А (записывается BÌА), если все элементы множества А₁ являются элементами А.

Для множеств определены следующие операции: объединение, пересечение, дополнение. Объединением множеств А и В (записывается AÈB) называется множество, состоящее из элементов как одного, так и второго множества. Например, А и В – множества точек, принадлежащих некоторым двум кругам, имеющим общие точки, тогда объединением AÈB будет фигура, состоящая из общих точек. Пересечением множеств А и В (записывается АÇВ) называется множество, состоящее из элементов, принадлежащих как одному, так и второму множеству одновременно. Дополнением множества А до В называется множество, состоящее из элементов множества В, не принадлежащих А. Дополнение обозначается C = В-А (рис. 3.1).

АÇВ

АÈВ

В-А

Рис. 3.1. Операции над множествами

Элементы теории графов

Граф задаётся парой множеств: множества Е, называемого множеством вершин, и множества U, называемого множеством рёбер. Ребро u Î U есть пара (е_i, е_j), где е_i, е_j Î Е , указывающая, между какими двумя вершинами проведено ребро. Говорят, что ребро u Î U инцидентно вершинам е_i, е_j. Если порядок рёбер не имеет значения, т.е. u =(е_i, е_j) =(е_j, е_i), то ребро называется неориентированным или просто ребром, если же порядок имеет значение, то ребро u = (е_i, е_j) называется ориентированным ребром или дугой. Вершина е_i называется началом дуги, е_j – конец дуги. Граф, содержащий хотя бы одну дугу, называется ориентированным графом или орграфом.

Граф G (E, U) называется конечным, если множество Е вершин конечно.

Граф G (E, U), у которого каждая вершина е_i Î Е соединена рёбрами с остальными вершинами (любые две вершены соединены ребром), называется полным (рис. 3.2).

Рис. 3.2. Полный граф

Если хотя бы две вершины соединены несколькими рёбрами, то такой граф называется мультиграфом. Две вершины е_i, е_j Î Е называются смежными, если они соединены ребром. Число рёбер, инцидентных данной вершине е_j, называется локальной степенью этой вершины р(е_i). Число рёбер r графа G(E,U) определяется выражением.

где n – количество вершин в графе.

Рассмотрим граф, изображённый на рисунке 3.3.

Рис. 3.3. Ориентированный граф

Множество вершин графа состоит из пяти элементов: Е = {1, 2, 3, 4, 5}, а множество рёбер U = {(1, 2), (1, 4), (1, 5), (2, 3), (3, 4), (5, 3)}. Ребро (5, 3) является ориентированным ребром или дугой. Число рёбер в графе определяется по значению локальных степеней для каждой вершины:

р(1) = 3; р(2) = 2; р(3) = 3; р(4) = 2; р(5) = 2; р = (3 + 2 + 3 + 2 + 2) / 2 = 6.

Важным в теории графов является понятие части графа G(E,U), который обозначается G'(E',U') Í G(E,U). Множества вершин и ребёр части графа являются подмножествами вершин и рёбер исходного графа Е'Í Е U'Í U. Многие задачи на графах состоят в определении частей графа с заданными свойствами.

Часть графа G'(E',U') Í G(E,U) называется подграфом графа G(E,U), если Е' Í Е, а подмножество U'ÍU образовано только рёбрами, инцидентными вершинам множества Е'.

Маршрутом графа G называется последовательность рёбер S = (u₁, u₂, ¼, u _n), в которой каждые два соседних ребра имеют общую вершину, т.е. u₁ = (е₁, е₂); u₂= (е₂, е₃); ... u _n = (е_n, е_n+1). Не исключено, что одно и то же ребро может встречаться несколько раз на одном маршруте.

Две вершины е_i и е_j называются связанными, если существует маршрут из е_i в е_j.

Простой цепью,или простым путём, называется маршрут, в котором ни одно ребро не повторяется дважды. Элементарной цепью или элементарным путём называется маршрут, в котором ни одна вершина не повторяется дважды. Циклом в графе называется маршрут, у которого начальная вершина совпадает с конечной. Например, граф, представленный на рисунке 3.4, имеет цикл S =(1, 2,3, 5, 4, 1).

Рис. 3.4. Пример графа, имеющего цикл

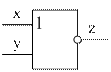
Цикл, проходящий по всем рёбрам графа только один раз, называется эйлеровым циклом. В теории графов доказывается теорема, определяющая, содержит ли граф эйлеров цикл. Оказывается, конечный граф содержит эйлеров цикл тогда и только тогда, когда он связан, и все его локальные степени вершин чётные. Важной прикладной задачей теории графов является задача поиска в графе цикла, проходящего через каждую вершину только один раз. Такие циклы называются гамильтоновыми циклами.

Весьма важным является связанный граф, не имеющий циклов, он называется деревом. В дереве любые две вершины связаны единственным путём. Вершина называется концевой, если ей инцидентно не более одного ребра; одна из концевых вершин может быть выбрана в качестве корня.

Теория графов используется в информатике и программировании, например, для представления структур данных (деревья), для моделирования сетей (маршрутизации данных в Интернете). В теории алгоритмов, блок-схема алгоритма − это ориентированный граф, указывающий порядок исполнения команд. Вершины такого графа могут быть одного из трёх типов, представленных в таблице 11.

Таблица 11