|
|
Определение в декартовых координатахПараметрическая форма Пусть на поверхности
заданных в ограниченной замкнутой области
Свойства Из определения поверхностного интеграла первого рода следует независимость этого интеграла от выбора ориентации векторного поля единичных нормалей к поверхности или, как говорят, от выбора стороны поверхности. Пусть функции 1. Линейность: 2. Аддитивность: 3. Монотонность: o если o для 4. Теорема о среднем для непрерывной функции
Поверхностный интеграл второго рода Определение Рассмотрим двустороннюю поверхность Для определенности предположим сначала, что поверхность задана явным уравнением Пусть теперь в точках данной поверхности
Конечный предел этой интегральной суммы при стремлении диаметров всех частей к нулю называют поверхностным интегралом второго рода от
распространенным на выбранную сторону поверхности
(здесь Если вместо плоскости
В приложениях чаще всего встречаются соединения интегралов всех этих видов:
где Связь между поверхностными интегралами второго и первого рода
Свойства Линейность: 1. Аддитивность: 2. При изменении ориентации поверхности, поверхностный интеграл меняет знак. #40)Фо́рмула Острогра́дского — математическая формула, которая выражает поток непрерывно-дифференцируемого векторного поля через замкнутую поверхность интегралом от дивергенции этого поля по объёму, ограниченному этой поверхностью: 3. 4. то есть интеграл от дивергенции векторного поля 5. Формула применяется для преобразования объёмного интеграла в интеграл по замкнутой поверхности. 6. В работе Остроградского формула записана в следующем виде: 7. 8. где 9. — функции, непрерывные вместе со своими частными производными первого порядка в замкнутой области пространства, ограниченного замкнутой гладкой поверхностью. 10. Обобщением формулы Остроградского является формула Стокса для многообразий с краем. #42)Теорема Стокса — одна из основных теорем дифференциальной геометрии и математического анализа об интегрировании дифференциальных форм, которая обобщает несколько теорем анализа Общая формулировка Пусть на ориентируемом многообразии
где Теорема распространяется на линейные комбинации подмногообразий одной размерности, так называемые цепи. В этом случае формула Стокса реализует двойственность между когомологией де Рама и гомологией циклов многообразия #43) В математическом анализе, производная по направлению — это обобщение понятия производной на случай функции нескольких переменных. Производная по направлению показывает, насколько быстро функция изменяется при движении вдоль заданного направления. Производная функции одной переменной показывает, как изменяется её значение при малом изменении аргумента. Если мы попытаемся по аналогии определить производную функции многих переменных, то столкнёмся с трудностью: в этом случае изменение аргумента (то есть точки в пространстве) может происходить в разных направлениях, и при этом будут получаться разные значения производной. Именно это соображение и приводит к определению производной по направлению. Рассмотрим функцию
Значение этого выражения показывает, как быстро меняется значение функции при сдвиге аргумента в направлении вектора Если направление сонаправленно с координатной осью, то производная по направлению совпадает с частной производной по этой координате. Связь с градиентом Производную по направлению дифференцируемой по совокупности переменных функции можно рассматривать как проекцию градиента функции на это направление, или иначе, как скалярное произведение градиента на орт направления:
Отсюда следует, что максимальное значение в точке производная по направлению принимает, если направление совпадает с направлением градиента функции в данной точке. Определение Для случая трёхмерного пространства градиентом скалярной функции
Или, использовав для единичных векторов по осям прямоугольных декартовых координат
Если
Используя интегральную теорему
градиент можно выразить в интегральной форме:
здесь #44)Поток векторного поля через поверхность — поверхностный интеграл второго рода по поверхности где
Иногда, особенно в физике, применяется обозначение
тогда поток записывается в виде
Определение Определение дивергенции выглядит так:
где ФF — поток векторного поля F через сферическую поверхность площадью S, ограничивающую объём V. Ещё более общим, а потому удобным в применении, является определение, когда форма области с поверхностью S и объёмом V допускается любой. Единственным требованием является её нахождение внутри сферы радиусом, стремящимся к нулю (то есть чтобы вся поверхность находилась в бесконечно малой окрестности данной точки, что нужно, чтобы дивергенция была локальной операцией и для чего очевидно недостаточно стремления к нулю площади поверхности и объёма ее внутренности). В обоих случаях подразумевается, что
Определение в декартовых координатах Допустим, что векторное поле дифференцируемо в некоторой области. Тогда в трёхмерном декартовом пространстве дивергенция будет определяться выражением
(здесь F - обозначено некое векторное поле с декартовыми компонентами Это же выражение можно записать с использованием оператора набла
Инвариантное определение дивергенции
Рассмотрим точку
Применяя к тройному интегралу теорему о среднем, получим
Здесь
В работе Остроградского формула записана в следующем виде:
где #45)Циркуля́цией ве́кторного по́ля по данному замкнутому контуру Γ называется криволинейный интеграл второго рода, взятый по Γ. По определению
где Математическое определение Ротор
Направление обхода контура выбирается так, чтобы, если смотреть в направлении В трёхмерной декартовой системе координат ротор (в соответствии с определением выше) вычисляется следующим образом (здесь F - обозначено некое векторное поле с декартовыми компонентами
или
(что можно считать альтернативным определением, по сути совпадающим с определением в начале параграфа, по крайней мере при условии дифференцируемости компонент поля). Для удобства можно формально представлять ротор как векторное произведение оператора набла (слева) и векторного поля:
Инвариантное определение ротора. Рассмотрим произвольную точку M в области V. Проведем через нее поверхность
Здесь, как и ранее
Это и есть инвариантное определение ротора. #47) Ортогональные криволинейные координаты В евклидовом пространстве особое значение имеет использование ортогональных криволинейных координат, поскольку формулы, имеющие отношение к длине и углам, выглядят в ортогональных координатах проще, нежели в общем случае. Что связано с тем, что метрическая матрица в системах с ортонормированным базисом будет диагональной, что существенно упростит расчёты. Цилиндрические координаты (n=3
Основная статья: Цилиндрические координаты Цилиндрические координаты являются тривиальным обобщением полярных на случай трёхмерного пространства путём добавления третьей координаты z. Связь цилиндрических координат с декартовыми:
Коэффициенты Ламе:
Дифференциал дуги:
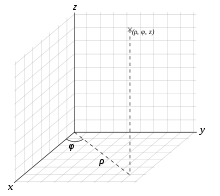
Сферические координаты (n=3
Основная статья: Сферические координаты Сферические координаты связаны с координатами широты и долготы на единичной сфере. Связь сферических координат с декартовыми:
Коэффициенты Ламе:
Дифференциал дуги:
Сферические координаты, как и цилиндрические, не работают на оси z {x=0, y=0}, поскольку координата φ там не определена. Определение Для случая трёхмерного пространства градиентом скалярной функции
Или, использовав для единичных векторов по осям прямоугольных декартовых координат
Если
#48) Цилиндрические координаты (n=3
Основная статья: Цилиндрические координаты Цилиндрические координаты являются тривиальным обобщением полярных на случай трёхмерного пространства путём добавления третьей координаты z. Связь цилиндрических координат с декартовыми:
Коэффициенты Ламе:
Дифференциал дуги:
Сферические координаты (n=3
Основная статья: Сферические координаты Сферические координаты связаны с координатами широты и долготы на единичной сфере. Связь сферических координат с декартовыми:
Коэффициенты Ламе:
Дифференциал дуги:
Сферические координаты, как и цилиндрические, не работают на оси z {x=0, y=0}, поскольку координата φ там не определена.
#1) Зависящий от параметра собственный интеграл Пусть в двумерном евклидовом пространстве задана область Пусть далее, Функция Непрерывность Пусть функция #2) Интегрирование под знаком интеграла Если функция
#3) Дифференцирование под знаком интеграла Пусть теперь на области Тогда #4) Несобственные интегралы I рода Пусть 1. Если 2. Если не существует конечного Пусть 1. Если 2. Если не существует конечного Если функция
|
|
 можно ввести единую параметризацию посредством функций
можно ввести единую параметризацию посредством функций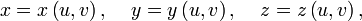
 плоскости
плоскости  и принадлежащих классу
и принадлежащих классу  в этой области. Если функция
в этой области. Если функция  непрерывна на поверхности
непрерывна на поверхности  , где:
, где: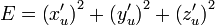
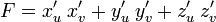
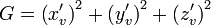
 и
и  интегрируемы по областям
интегрируемы по областям  :
: для любых вещественных чисел
для любых вещественных чисел  ;
; при условии, что
при условии, что  и
и  не имеют общих внутренних точек;
не имеют общих внутренних точек; , то
, то 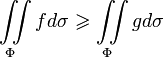
 если
если  , то
, то 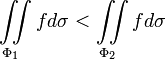
 , где
, где  , а
, а  — площадь области
— площадь области  .
. причем точка
причем точка  изменяется в области
изменяется в области  на плоскости
на плоскости  , ограниченный кусочно-гладким контуром.
, ограниченный кусочно-гладким контуром. и выбрав на каждой такой части точку
и выбрав на каждой такой части точку  вычисляем значение функции
вычисляем значение функции  в данной точке и умножим его на площадь
в данной точке и умножим его на площадь  проекции на плоскость
проекции на плоскость  , снабженную определенным знаком. Составим интегральную сумму:
, снабженную определенным знаком. Составим интегральную сумму: .
. ,
,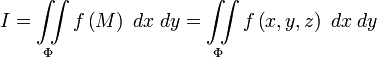
 ) напоминает о площади проекции элемента поверхности на плоскость
) напоминает о площади проекции элемента поверхности на плоскость 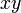
 или
или  , то получим два других поверхностных интеграла второго типа:
, то получим два других поверхностных интеграла второго типа: или
или  .
.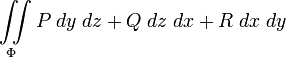
 суть функции от
суть функции от  , определенные в точках поверхности
, определенные в точках поверхности  , где
, где  — единичный вектор нормали поверхности
— единичный вектор нормали поверхности  ,
,  — орт.
— орт. ;
; ;
;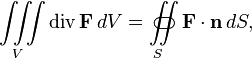
 , распространённый по некоторому объёму
, распространённый по некоторому объёму 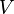 , равен потоку вектора через поверхность
, равен потоку вектора через поверхность  , ограничивающую данный объём.
, ограничивающую данный объём.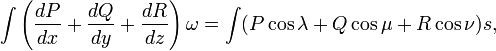
 и
и  — дифференциалы объёма и поверхности соответственно. В современной записи
— дифференциалы объёма и поверхности соответственно. В современной записи  — элемент объёма,
— элемент объёма,  — элемент поверхности.
— элемент поверхности. размерности
размерности  заданы ориентируемое
заданы ориентируемое  -мерное подмногообразие
-мерное подмногообразие  и дифференциальная форма
и дифференциальная форма  класса
класса  (
(  ). Тогда, если граница подмногообразия
). Тогда, если граница подмногообразия  положительно ориентирована, то
положительно ориентирована, то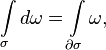
 обозначает внешний дифференциал формы
обозначает внешний дифференциал формы  от
от  аргументов в окрестности точки
аргументов в окрестности точки  . Для любого единичного вектора
. Для любого единичного вектора  определим производную функции
определим производную функции  по направлению
по направлению  следующим образом:
следующим образом:
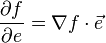
 координат
координат  ,
, 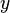 ,
,  называется векторная функция с компонентами
называется векторная функция с компонентами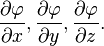
 :
: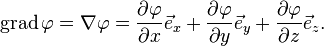
 — функция
— функция 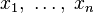 , то её градиентом называется
, то её градиентом называется 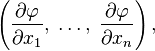
 ,
, ,
, — замкнутая поверхность охватывающая объём
— замкнутая поверхность охватывающая объём  — нормальный элемент этой поверхности.
— нормальный элемент этой поверхности.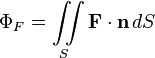
 — векторное поле (вектор-функция векторного аргумента — точки пространства),
— векторное поле (вектор-функция векторного аргумента — точки пространства),  — единичный вектор положительной нормали к поверхности (положительное направление выбирается для ориентируемой поверхности условно, но одинаково для всех точек — то есть для дифференцируемой поверхности — так, чтобы
— единичный вектор положительной нормали к поверхности (положительное направление выбирается для ориентируемой поверхности условно, но одинаково для всех точек — то есть для дифференцируемой поверхности — так, чтобы  — элемент поверхности.
— элемент поверхности. , а поверхностью является обычная двумерная поверхность.
, а поверхностью является обычная двумерная поверхность.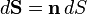
 .
.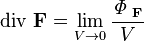
 .
.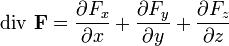
 ):
):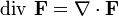
 (рис. 3), окружим ее замкнутой поверхностью
(рис. 3), окружим ее замкнутой поверхностью  и вычислим поток поля
и вычислим поток поля  через эту поверхность по формуле Остроградского
через эту поверхность по формуле Остроградского
 .
. или
или  .
. есть некоторая точка из области
есть некоторая точка из области  . В последнем равенстве перейдем к пределу, стягивая область
. В последнем равенстве перейдем к пределу, стягивая область  будет стремиться к точке
будет стремиться к точке 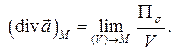

 — векторное поле (или вектор-функция), определенное в некоторой области D, содержащей в себе контур Γ,
— векторное поле (или вектор-функция), определенное в некоторой области D, содержащей в себе контур Γ,  — бесконечно малое приращение радиус-вектора
— бесконечно малое приращение радиус-вектора  вдоль контура. Окружность на символе интеграла подчёркивает тот факт, что интегрирование производится по замкнутому контуру. Приведенное выше определение справедливо для трёхмерного случая, но оно, как и основные свойства, перечисленные ниже, прямо обобщается на произвольную размерность пространства.
вдоль контура. Окружность на символе интеграла подчёркивает тот факт, что интегрирование производится по замкнутому контуру. Приведенное выше определение справедливо для трёхмерного случая, но оно, как и основные свойства, перечисленные ниже, прямо обобщается на произвольную размерность пространства. векторного поля
векторного поля  — есть вектор, проекция которого
— есть вектор, проекция которого  на каждое направление n есть предел отношения циркуляции векторного поля по контуру L, являющемуся краем плоской площадки ΔS, перпендикулярной этому направлению, к величине этой площадки, когда размеры площадки стремятся к нулю, а сама площадка стягивается в точку:
на каждое направление n есть предел отношения циркуляции векторного поля по контуру L, являющемуся краем плоской площадки ΔS, перпендикулярной этому направлению, к величине этой площадки, когда размеры площадки стремятся к нулю, а сама площадка стягивается в точку: .
. - орты декартовых координат):
- орты декартовых координат):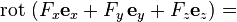

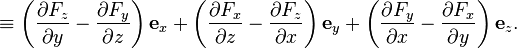
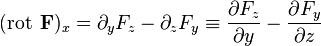
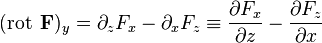
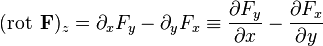
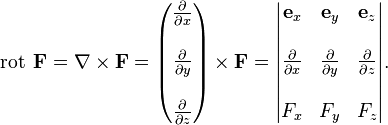
 , границей которой служит контур
, границей которой служит контур  . Пусть поверхность и контур удовлетворяют условиям теоремы Стокса. По теореме о среднем для поверхностного интеграла и формуле Стокса получим
. Пусть поверхность и контур удовлетворяют условиям теоремы Стокса. По теореме о среднем для поверхностного интеграла и формуле Стокса получим .
.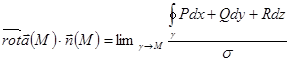
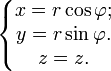
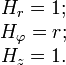
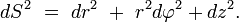
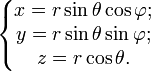

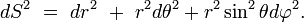
 , на которой определена функция
, на которой определена функция  двух переменных.
двух переменных. .
. и называется интегралом, зависящим от параметра.
и называется интегралом, зависящим от параметра. как функция двух переменных. Тогда функция
как функция двух переменных. Тогда функция  непрерывна на отрезке
непрерывна на отрезке  .
. , или, что то же самое:
, или, что то же самое: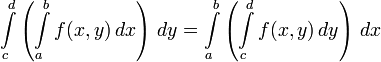
 .
. , или, что то же самое,
, или, что то же самое, 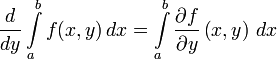
 определена и непрерывна на интервале
определена и непрерывна на интервале  и
и  . Тогда:
. Тогда: , то используется обозначение
, то используется обозначение  и интеграл называется несобственным интегралом Римана первого рода. В этом случае
и интеграл называется несобственным интегралом Римана первого рода. В этом случае  (
(  или
или  ), то интеграл
), то интеграл  называется расходящимся к
называется расходящимся к  , или просто расходящимся.
, или просто расходящимся. и
и  . Тогда:
. Тогда: , то используется обозначение
, то используется обозначение  и интеграл называется несобственным интегралом Римана первого рода. В этом случае
и интеграл называется несобственным интегралом Римана первого рода. В этом случае  (
(  называется расходящимся к
называется расходящимся к  , где с — произвольное число.
, где с — произвольное число.