|
|
Геометрический смысл несобственного интеграла I родаНесобственный интеграл первого рода выражает площадь бесконечно длинной криволинейной трапеции. Примеры
Несобственные интегралы II рода Пусть 1. Если 2. Если Пусть 1. Если 2. Если Если функция
Геометрический смысл несобственных интегралов II рода Несобственный интеграл второго рода выражает площадь бесконечно высокой криволинейной трапеции Пример
Критерий Коши 1. Пусть Тогда 2. Пусть Тогда Абсолютная сходимость Интеграл Условная сходимость Интеграл #9) Интегральное определение Если вещественная часть комплексного числа
Это определение было получено Лежандром из оригинального определения Эйлера
полученного им в 1730 г., через замену переменной, и на сегодняшний день, именно определение Лежандра известно как «классическое» определение гамма-функции. Интегрируя по частям классическое определение, легко видеть что для целых n имеем Существует непосредственное аналитическое продолжение исходной формулы на всю комплексную плоскость, называемое интегралом Римана-Ханкеля
где контур Последующие выражения служат альтернативными определениями Гамма-функции. Свойства
График модуля гамма-функции на комплексной плоскости. Основное свойство гамма-функции — это её рекуррентное уравнение
которое, при фиксированном начальном условии, единственным образом определяет логарифмически выпуклое решение, то есть саму гамма-функцию. Теорема о единственности.
И формула умножения Гаусса:
Частный случай которой при n=2 был получен Лежандром:
Гамма-функция не имеет нулей на всей комплексной плоскости.
Основное, но полезное свойство, которое может быть получено из предельного определения:
Гамма-функция дифференцируема бесконечное число раз, и #10) В математике бета-функцией (
определённая при Свойства Бета-функция симметрична относительно перестановки переменных, то есть
Бета-функцию можно выразить через другие функции:
где
где Подобно тому как гамма-функция для целых чисел является обобщением факториала, бета-функция является обобщением биномиальных коэффициентов с немного изменёнными параметрами:
#11) Гамма-функция и бета-функция связаны следующим соотношением:
#12) Преобразование Фурье функции
#15) Двойной интеграл
Геометрический смысл двойного интеграла Двойным интегралом называют кратный интеграл с
В прямоугольных координатах: |
|
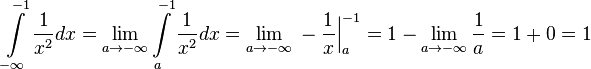
 определена на
определена на  , терпит бесконечный разрыв в точке x=a и
, терпит бесконечный разрыв в точке x=a и  . Тогда:
. Тогда: , то используется обозначение
, то используется обозначение  и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся. или
или  , то обозначение сохраняется, а
, то обозначение сохраняется, а  называется расходящимся к
называется расходящимся к  , или просто расходящимся.
, или просто расходящимся. , терпит бесконечный разрыв при x=b и
, терпит бесконечный разрыв при x=b и  . Тогда:
. Тогда: отрезка
отрезка  , то несобственный интеграл второго рода определяется формулой:
, то несобственный интеграл второго рода определяется формулой:
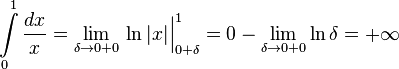
 и
и  .
.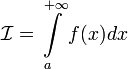 сходится
сходится 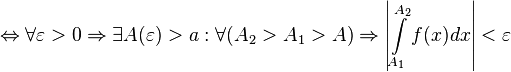
 .
.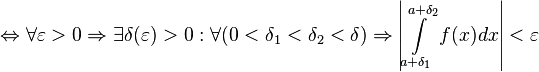
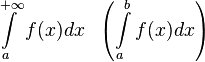 называется абсолютно сходящимся, если
называется абсолютно сходящимся, если  сходится.
сходится. называется условно сходящимся, если
называется условно сходящимся, если  расходится.
расходится. положительна, то Гамма-функция определяется через абсолютно сходящийся интеграл
положительна, то Гамма-функция определяется через абсолютно сходящийся интеграл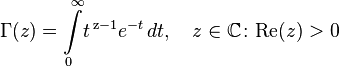
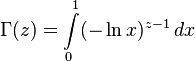
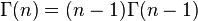 , и вообще
, и вообще 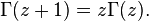
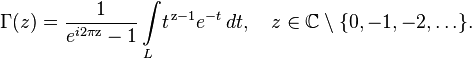
 — любой контур на комплексной плоскости, обходящий точку
— любой контур на комплексной плоскости, обходящий точку 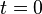 против часовой стрелки, концы которого уходят на бесконечность вдоль положительной вещественной оси.
против часовой стрелки, концы которого уходят на бесконечность вдоль положительной вещественной оси.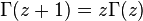
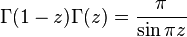 .
.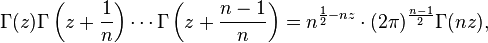
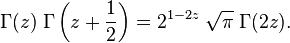
 является мероморфной на комплексной плоскости и имеющей простые полюса в точках
является мероморфной на комплексной плоскости и имеющей простые полюса в точках  Гамма-функция имеет полюс первого порядка в
Гамма-функция имеет полюс первого порядка в 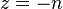 для любого натурального
для любого натурального  и нуля; вычет в этой точке задается так
и нуля; вычет в этой точке задается так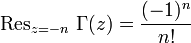 .
. .
. , где
, где  часто называют «пси-функцией», или дигамма-функцией
часто называют «пси-функцией», или дигамма-функцией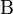 -функцией, бета-функцией Эйлера или интегралом Эйлера I рода) называется следующая специальная функция от двух переменных:
-функцией, бета-функцией Эйлера или интегралом Эйлера I рода) называется следующая специальная функция от двух переменных: ,
, ,
,  .
. .
. ,
, — Гамма-функция;
— Гамма-функция;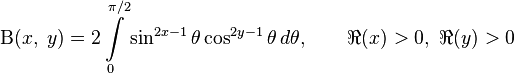 ;
; ;
; ,
, — нисходящий факториал, равный
— нисходящий факториал, равный  .
. .
. .
. вещественной переменной является интегральным и задаётся следующей формулой:
вещественной переменной является интегральным и задаётся следующей формулой: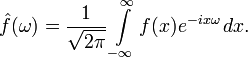
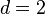 .
. . Здесь
. Здесь  — элемент площади в рассматриваемых координатах.
— элемент площади в рассматриваемых координатах. , где
, где 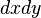 — элемент площади в прямоугольных координатах.
— элемент площади в прямоугольных координатах.