|
|
Графический метод решения задачи линейного программирования с двумя переменными
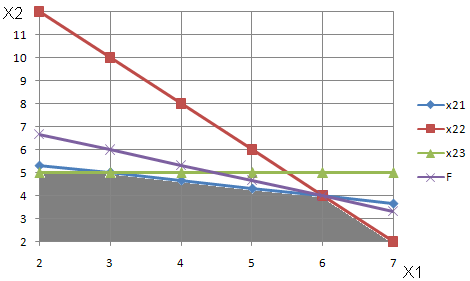
Достаточно просто задача линейного программирования с двумя переменными решается графическим методом. Понимание этого метода позволяет проанализировать влияние отдельных ограничений. Рассмотрим этот метод на примере задачи, представленной в одном из предшествующих подразделов таблицей 1 и выражениями (1) и (2). Для начала в прямоугольной системе координат х1 х2 построим прямые, по преобразованным уравнениям, полученным из системы (1) путём замены знака неравенства на равенство.
Эти прямые являются границами множества точек х1 х2, удовлетворяющих неравенству (1). Соответствующая область допустимых решений выделена серым цветом. Для поиска оптимального решения выразим из (2) следующее уравнение x2= (F – 2x1)/3. (4) Отметим, что угол наклона этой прямой не зависит от искомой величины F. А максимальному значению F будет соответствовать прямая (фиолетовая), проходящая через точку пересечения ограничений, представленных синей и красной прямыми. То есть оптимальному решению соответствует решение следующей системы уравнений
Так как именно первые два ограничения оказываются лимитирующими (связывающими). Поэтому именно два первых вида ресурсов в данном примере оказываются «критическими», именно их запасы ограничивают возможности дальнейшего роста прибыли. Зачастую графическая интерпретация позволяет убедиться в том, что оптимальное решение не может быть получено из-за того, что модель является неограниченной (ограничение пропущено), либо наоборот, вообще не имеет допустимых решений из-за несовместимых ограничений.
АППРОКСИМАЦИЯ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
Теоретические основы
На практике часто приходится сталкиваться с задачей экспериментальных зависимостей или задачей аппроксимации. Напомним, что аппроксимацией называется процесс подбора эмпирической формулы Обычно задача аппроксимации распадается на две части. Сначала устанавливают вид зависимости После выбора вида формулы определяют ее параметры. Для наилучшего выбора параметров задают меру близости аппроксимации экспериментальных данных. Во многих случаях, в особенности, если функция Используя методы дифференциального исчисления, метод наименьших квадратов формулирует аналитические условия достижения суммой квадратов отклонений (1.1) своего наилучшего значения. Так, если функция
(1.2)
В нашем случае задача аппроксимации экспериментальных данных выглядит следующим образом. Пусть есть данные о продажах на предприятии за каждый день, которые можно представить парами чисел (x, y). Зависимость между ними отражает таблица. Исходные данные в тыс. руб.
На основе этих данных требуется подобрать функцию Выяснить вид функции можно либо из теоретических соображений, либо анализируя расположение точек Учитывая, что практические данные были получены с некоторой погрешностью, обусловленной округлением до тысяч рублей и т.п., естественно предположить, что здесь имеет место линейная зависимость
Менеджер должен четко понимать, нужно ли для решения конкретной проблемы приобретать специализированное программное обеспечение или имеющиеся средства MS Office более надежны, доступны и удобны для пользователя. Менеджер должен принять экономически эффективное решение, обеспечивающее максимальную прибыль при минимальных суммарных затратах. В MS Excel аппроксимация экспериментальных данных осуществляется путем построения графика (х – отвлеченные величины) или точечного графика (х – имеет конкретные значения) с последующим подбором подходящей аппроксимирующей функции (линии тренда). В нашем случае рассмотрим два варианта функции: 1. Линейная – 2. Полиномиальная – Степень близости аппроксимации экспериментальных данных выбранной функции оценивается коэффициентом детерминации (R2). Таким образом, если есть несколько подходящих вариантов типов аппроксимирующих функций, можно выбрать функцию с большим коэффициентом детерминации (стремящимся к 1). Линейная регрессия
Так как задача отыскания функциональной зависимости очень важна, то в MS Excel введен набор функций, которые позволяют решить эту задачу. Эти функции основаны на методе наименьших квадратов. Но регрессионный анализ – это не только метод наименьших квадратов. Относительно исходных данных делаются некоторые статистические предположения. В качестве результата выдаются не только коэффициенты функции, приближающие данные, но и статистические характеристики полученных результатов. Исходные предположения таковы. Считается, что зависимость между откликом и факторами имеет вид Решим задачу выбора линейной функции с помощью функций Excel, предназначенных для расчета линейной регрессии. Занесем исходные данные на рабочий лист в блок B2:К3. Воспользуемся функцией
ЛИНЕЙН(известные_значения_у;известные_значения_х;конст;статистика)
В нашем случае известные_значения_у находятся в диапазоне B3:К3, а известные_значения_х – в диапазоне B2:К2. Два последних аргумента – логические. Если аргумент конст – ИСТИНА или опущен, то свободный член в регрессионном уравнении может быть любым, а если конст – ЛОЖЬ, то b принудительно полагается равным нулю. Последний аргумент, статистика, определяет, выдаются ли дополнительные статистические характеристики (ИСТИНА), или нет (ЛОЖЬ или опущен). Вместо логических значений Истина и ЛОЖЬ можно вводить числовые аргументы 1 и 0, что намного удобнее. Так как функция возвращает сразу несколько значений, формулу с этой функцией надо вводить как табличную. Так как мы хотим вывести полную статистику, то нужно выделить блок из пяти строк и двух столбцов. Выделим блок А5:В9, щелкнем по кнопке со знаком равенства, в Мастере функций выберем в категории Статистические функцию ЛИНЕЙН и заполним появившееся диалоговое окно, как показано на рисунке 1.2. Первым аргументом укажем блок В3:К3, вторым аргументом – блок В2:К2, в третьем и четвертом поле ввода проставим 1. Не щелкаем по кнопке ОК, а нажимаем Ctrl+Shift+Enter (находясь в диалоговом окне!). Получим следующую таблицу, представленную на рисунке 1.3.
Рис. 1.2. Диалоговое окно функции ЛИНЕЙН
В ячейку А5 записан коэффициент a, в В5 – коэффициент b. Ниже, в ячейках А6 и В6, соответственно, записаны стандартные отклонения (т.е. среднеквадратические отклонения, или корни квадратные из дисперсии) для этих коэффициентов. В ячейку A7 записан так называемый коэффициент детерминации R2. Этот коэффициент лежит на отрезке [0;1]. Считается, что чем ближе коэффициент к 1, тем лучше регрессионное уравнение. Далее мы убедимся, что к такой интерпретации надо относиться «осторожно». В ячейке В7 находится стандартная ошибка для оценки у. В ячейку А8 записано значение F-статистики, а в В8 – количество степеней свободы. Число степеней свободы нужно для расчета критических значений F-статистики. В последней строке таблицы записаны регрессионная сумма квадратов и остаточная сумма квадратов. Итак, у нас получились коэффициенты регрессии 4,78 и 1783,13, т.е. прямая у=4,78х+1783,13. На рисунке 1.4 представлена диаграмма с исходными данными и приближающим их линейным графиком. Отклонения данных от графика показаны вертикальными отрезками.
Рис. 1.4. График регрессионной модели
Для оценки качества регрессионной модели надежнее всего оценивать остатки. Для этого воспользуемся инструментом Excel Сценарии.
|
|
 (3)
(3)
 ,
,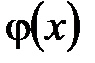 для установленной из опыта функциональной зависимости
для установленной из опыта функциональной зависимости  . Эмпирические формулы служат для аналитического представления опытных данных.
. Эмпирические формулы служат для аналитического представления опытных данных. и, следовательно, вид эмпирической формулы, т.е. решают, является ли она линейной, квадратичной, логарифмической или какой-либо другой. После этого определяются численные значения неизвестных параметров выбранной эмпирической формулы, для которых приближение к заданной функции оказывается наилучшим. Если нет каких-либо теоретических соображений для подбора вида формулы, обычно выбирают функциональную зависимость из числа наиболее простых, сравнивая графики с графиком заданной функции.
и, следовательно, вид эмпирической формулы, т.е. решают, является ли она линейной, квадратичной, логарифмической или какой-либо другой. После этого определяются численные значения неизвестных параметров выбранной эмпирической формулы, для которых приближение к заданной функции оказывается наилучшим. Если нет каких-либо теоретических соображений для подбора вида формулы, обычно выбирают функциональную зависимость из числа наиболее простых, сравнивая графики с графиком заданной функции. задана графиком или таблицей (на дискретном множестве точек), для оценки степени приближения рассматривают разности
задана графиком или таблицей (на дискретном множестве точек), для оценки степени приближения рассматривают разности  для точек
для точек 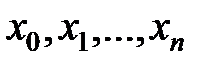 . Существуют различные меры близости и, соответственно, способы решения этой задачи. Некоторые из них просты, быстро приводят к результату, но результат этот является сильно приближенным. Другие более точные, но и более сложные. Обычно определение параметров при неизвестном виде зависимости осуществляют по методу наименьших квадратов. При этом функция
. Существуют различные меры близости и, соответственно, способы решения этой задачи. Некоторые из них просты, быстро приводят к результату, но результат этот является сильно приближенным. Другие более точные, но и более сложные. Обычно определение параметров при неизвестном виде зависимости осуществляют по методу наименьших квадратов. При этом функция 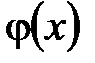 считается наилучшим приближением к
считается наилучшим приближением к  , если для нее сумма квадратов невязок
, если для нее сумма квадратов невязок  или отклонений «теоретических» значений
или отклонений «теоретических» значений  , найденных по эмпирической формуле, от соответствующих опытных значений yi, имеет наименьшее значение по сравнению с другими функциями, из числа которых выбирается искомое приближение.
, найденных по эмпирической формуле, от соответствующих опытных значений yi, имеет наименьшее значение по сравнению с другими функциями, из числа которых выбирается искомое приближение. (1.1)
(1.1)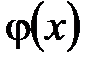 вполне определяется своими параметрами k, l, m,…, то наилучшие (в указанном смысле 1.1) значения эти параметров находятся из решения системы уравнений. Например, в простейшем случае, когда функция
вполне определяется своими параметрами k, l, m,…, то наилучшие (в указанном смысле 1.1) значения эти параметров находятся из решения системы уравнений. Например, в простейшем случае, когда функция  представлена линейным уравнением
представлена линейным уравнением 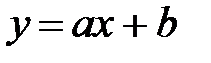 , система имеет вид:
, система имеет вид:

 , которая наилучшим образом сглаживала бы экспериментальную зависимость между переменными и, по возможности, точно отражала общую тенденцию зависимости между x и у, исключая погрешности измерений и случайные отклонения. Это значит, что отклонения
, которая наилучшим образом сглаживала бы экспериментальную зависимость между переменными и, по возможности, точно отражала общую тенденцию зависимости между x и у, исключая погрешности измерений и случайные отклонения. Это значит, что отклонения  , в каком-то смысле были бы наименьшими.
, в каком-то смысле были бы наименьшими. на координатной плоскости. Расположение экспериментальных точек может иметь самый различный вид. В нашем случае точки расположены, как показано на рисунке 1.1.
на координатной плоскости. Расположение экспериментальных точек может иметь самый различный вид. В нашем случае точки расположены, как показано на рисунке 1.1. Рис. 1.1. График расположения экспериментальных точек
Рис. 1.1. График расположения экспериментальных точек , где до шестого порядка включительно (n£6), ai – константы. Используется для описания экспериментальных данных, попеременно возрастающих и убывающих. Степень полинома определяет количество экстремумов (максимумов или минимумов) кривой. Полином второй степени может описать только один максимум или минимум, полином третьей степени может иметь один или два экстремума, четвертой степени – не более трех экстремумов и т.д.
, где до шестого порядка включительно (n£6), ai – константы. Используется для описания экспериментальных данных, попеременно возрастающих и убывающих. Степень полинома определяет количество экстремумов (максимумов или минимумов) кривой. Полином второй степени может описать только один максимум или минимум, полином третьей степени может иметь один или два экстремума, четвертой степени – не более трех экстремумов и т.д. , где e – некоторая случайная величина. Именно из-за нее возникают ненулевые остатки ei. В гауссовской модели простой линейной регрессии предполагается, что ei независимы и распределены по нормальному закону с нулевым средним и одинаковой дисперсией.
, где e – некоторая случайная величина. Именно из-за нее возникают ненулевые остатки ei. В гауссовской модели простой линейной регрессии предполагается, что ei независимы и распределены по нормальному закону с нулевым средним и одинаковой дисперсией.
 Рис. 1.3. Статистические оценки регрессионной модели
Рис. 1.3. Статистические оценки регрессионной модели