Модели принятия решений в условиях определённости, риска и неопределённости

Отсутствие определённости относительно будущих событий – характерная черта многих управленческих решений. Далеко не всегда можно предсказать изменения, которые произойдут в будущем, а уж тем более – учесть всё их влияние. Зачастую менеджер, анализируя при принятии решения реальную ситуацию, может с полной определённостью прогнозировать только одно – то, что изменения обязательно будут.

В теории принятия решений предлагаются свои подходы к анализу ситуаций, характеризующихся различным уровнем предсказуемости и определённости, основанные на использовании вероятностных моделей. Далее будут представлены три класса моделей, соответствующих принятию решений в условиях определённости, риска и неопределённости.

Так, в рассмотренных ранее примерах задач линейного программирования были неизвестны только переменные решения, а сама модель являлась детерминированной, определённой. То есть известны все функции (целевая, ограничений) и значения соответствующих коэффициентов, параметров. Решение полностью определяется набором контролируемых переменных. При одних и тех же значениях переменных решения мы получим один и тот же результат.

Такие модели можно рассматривать как модели принятия решений в условиях определённости. Определённость ситуации можно охарактеризовать одним-единственным состоянием бизнес-среды (формального мира, природы) и соответствующим набором значений неконтролируемых параметров, известным до принятия решения. Вероятность того, что среда находится в этом состоянии, равна единице.

В реальном мире, конечно же, течение большинства событий подвержено некоторой неопределённости, непредсказуемости ситуации, которая характеризуется не единственным, а несколькими возможными состояниями. И во многих случаях этим нельзя пренебрегать.

Модель принятия решений может быть основана на так называемой таблице платежей (выигрышей, проигрышей), в которой представлены значения платежа П_ij для всех возможных комбинаций решений Р_i и состояний бизнес-среды C_j. С помощью такой таблицы можно выбрать наилучшее решение для каждого из возможных состояний. В моделях принятия решений в условиях определённости размер такой таблицы, определяющий сложность её создания и анализа, зависит только от множества допустимых решений. Поскольку состояние среды единственное, то оптимальному решению соответствует максимальное значение платежа.

Если возможных состояний среды несколько, то задача осложняется не только увеличением размера содержательной части таблицы (во столько же раз, во сколько увеличится число состояний), но ещё и выбором критерия оптимальности, учитывающего различные состояния для каждого решения.

Модели принятия решений в условиях риска основаны на предположении, что известны вероятности p_j каждого из возможных состояний среды, соответствующих ситуации. В этом случае критерием оптимальности может служить ожидаемый результат ОР_i от принятия i-го решения, определяемый формулой

(1)

Следовательно, следует выбрать такое решение, для которого ожидаемый результат окажется максимальным.

В моделях принятия решений в условиях неопределённости вероятности появления каждого из возможных состояний среды вообще неизвестны. Поэтому для выбора приемлемого решения либо их предполагают равными, как при использовании критерия Лапласса, что не всегда верно. Либо предпочтение отдаётся «лучшему из худших», как при использовании максиминного критерия (выбирается решение, соответствующее максимальному значению минимального платежа, определяемого по каждому из возможных состояний), что позволяет избежать реализации наихудшего варианта. Либо выбирается решение, соответствующее максимально возможному платежу, как при использовании максимаксного критерия. Либо, как при использовании критерия минимаксных потерь, оптимальность решения оценивается по таблице потерь, значения которой получаются для каждого состояния путём вычитания текущего значения платежа из максимального. Это тоже соответствует «лучшему из худших» вариантов, но уже по отношению к потерям.

Моделирование киоска

Для иллюстрации материала предыдущего подраздела создадим и проанализируем модель некоего ларька скоропортящихся товаров. Предположим, продавец может рано утром приобрести товар по 40 денежных единиц за одну штуку и реализовать его в течение дня по 75. Это «благородное дело» может, конечно, принести прибыль. Но продавец, закупая товар, не может знать, какое именно количество товара потребуется покупателям, то есть какой будет спрос, поэтому возможны и убытки. Так, если он закупит больше, чем сможет продать, то убытки равны закупочной стоимости нереализованного товара. А если закупит слишком мало, то обобщённые потери от появления каждого из неудовлетворённых покупателей составят, предположим, 50 единиц (например, продавец захочет удержать клиента и понесёт дополнительные расходы, изыскивая иные возможности удовлетворить спрос, либо он потеряет клиента, а вместе с ним упустит возможность получить от него выгоду в будущем).

Предположим, что продавец смог несколько уменьшить непредсказуемость ситуации, определив все возможные состояния, соответствующие четырем значениям спроса: 0, 1, 2 и 3 покупателя в день. Продавец также оценил соответствующие спросу вероятности следующим образом: p₀=0,1; p₁=0,3; p₃=0,4; p₄=0,2.

Создадим модель принятия решений в условиях риска, построив соответствующую таблицу платежей и дополнив её строкой значений вероятностей спроса и столбцом ожидаемых платежей.

Таблица 1

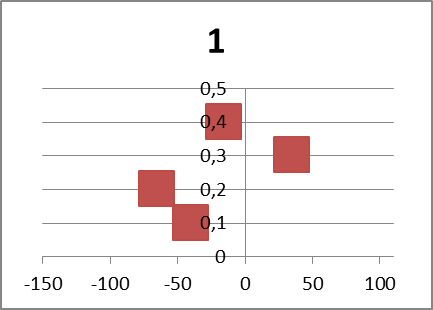
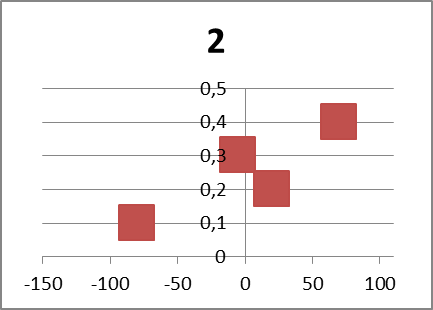
Напомним, что основная часть таблицы представляет собой значения платежа П_ij для всех возможных комбинаций объёма закупки и спроса. Поясним также, что платежи вычисляются по следующей формуле:

П_ij = 75*(У_ij) - 40*(Р_i) - 50*(Н_ij), (2)

где У_ij – количество проданных товаров, то есть удовлетворённый спрос, это значение равно объему закупки, если спрос превышает предложение (и поэтому возникает неудовлетворённый спрос), иначе – спросу; Н_ij – неудовлетворённый спрос, это значение равно нулю, если спрос не превышает предложения, иначе – разности спроса и предложения; отметим, что объемы закупки Р_i представляют собой переменные решения, и большие их значения не рассматривались ввиду очевидной нецелесообразности, хотя заинтересованный читатель, возможно, будет удивлён, узнав неочевидный факт – решение о закупке четырёх товаров оказывается хоть и убыточным, но всё-таки лучшим (платёж -32,5), чем бездействовать (платёж -85).

Ожидаемый платёж определяется по формуле (1). Таким образом, используя критерий максимального ожидаемого результата (платеж 22,5 ед.) следует принять решение о ежедневной закупке товара в количестве 2 шт.

Некоторые менеджеры предпочитают анализировать также графики так называемых профилей рисков, которые наглядно представляют информацию из таблицы платежей и отображают для каждого решения возможные платежи и их вероятности. Например, график 0 не содержит ни одного положительного платежа. График 1 – только один, и то не наиболее вероятный. Графики 2 и 3 отображают уже по два положительных платежа, при этом максимальному платежу на графике 2 соответствует и наибольшая вероятность.

Вернёмся к табличной модели ларька и покажем, как её можно использовать в условиях неопределённости. Основная часть таблицы не изменится. Использование различных критериев приведёт к разным результатам.

При использовании критерия Лапласса в формулу (1) следует подставить значения вероятностей, равные 0,25. Это также позволит принять решение о ежедневной закупке товара в количестве 2 шт., но уже с ожидаемым значением платежа 1,25 ед.

Другие критерии не используют значения вероятностей и ожидаемого результата. Использование «пессимистичного» максиминного критерия предполагает отыскание минимальных (наихудших) платежей по каждому возможному решению в таблице (-150; -65; -80; -120) и выборе из них максимального (-65), что соответствует купле и продаже только одной штуки товара. А вот использование «оптимистичного» максимаксного критерия, игнорирующего потери и предполагающего получение по каждому решению только максимального результата (0; 35; 70; 105), приведёт к принятию решения о закупке товара в количестве 3 шт.

Для использования критерия минимаксных потерь следует составить таблицу, в которой значения потерь для каждого решения определяются из таблицы платежей по каждому состоянию спроса (по столбцам) как разность максимального и текущего платежей, соответствующих спросу.

После чего по каждому решению отыскиваются максимальные значения потерь (255; 170; 85; 120), из которых выбирается минимальное (85), что соответствует решению о объёмах закупки 2 шт.

Как видно, разные критерии приводят к разным решениям одних и тех же задач, особенно в условиях неопределённости. Это приводит к внесению субъективности в принимаемые решения, связанной с выбором используемого критерия оптимальности. Поэтому маркетинговые компании тратят большие суммы на то, чтобы выяснить возможные состояния среды и внести определённость в исследуемые бизнес-проекты.

Отметим, что принятие решений в условиях риска оперирует вероятностями возможных состояний, что характеризует неопределённость ситуации. Это можно (и нужно) использовать, но на это нельзя повлиять. То есть, принятие решений никак не изменит случайность ситуации – она, как будто, определяется неким игроком, действующим безразлично. Что тоже в реальном мире может не наблюдаться. Этим теория принятия решений отличается от теории игр, в которой игроки действуют в своих интересах, преследуют определённые цели и, конечно же, решения других игроков им далеко не безразличны, особенно если они оказывают влияние на ситуацию.

ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ