|
|
Свойства опрераций над матрицамиВычисление определителей II и III порядка Определителем называется число, записанное в виде квадратной таблицы: Определитель II порядка вычисляется по формуле: Определитель III порядка можно вычислить по правилу Сарруса:
Основные свойства определителей: 1.1. Значение определителя не изменится, если: 1) строки заменить на столбцы, такое действие называется транспонирование, т.е. действия, выполняемые со строками, справедливы и для столбцов; все элементы одной строки умножить на какое-либо число и прибавить к соответствующим элементам другой строки. Такие действия с элементами определителя называются элементарными преобразованиями. 2)Определитель меняет знак на противоположный, если две каких-либо строки поменять местами. 3)Определитель равен нулю, если: - все элементы какой-либо строки равны нулю; - соответствующие элементы каких-либо двух строк равны; - соответствующие элементы каких-либо двух строк пропорциональны. Минор и алгебраическое дополнение Минором Решение. Вычеркиваем в заданном определителе вторую строку и третий столбец:
тогда Ответ. Алгебраическое дополнение Алгебраическим дополнением Пример Задание. Найти алгебраическое дополнение Решение. Ответ. 4)Правило Крамера Пусть матричное уравнение AX = B описывает систему n линейных уравнений с n неизвестными.Если где
5) Действия над матрицамии их свойства. 1. Сложение матриц - поэлементная операция
2. Вычитание матриц - поэлементная операция
3. Произведение матрицы на число - поэлементная операция
4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B) Amk*Bkn=Cmn причем каждый элемент сijматрицы Cmn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы B , т.е.
Покажем операцию умножения матриц на примере
5. Возведение в степень
m>1 целое положительное число. А - квадратная матрица (m=n) т.е. актуально только для квадратных матриц 6. Транспонирование матрицы А. Транспонированную матрицу обозначают AT или A'
Строки и столбцы поменялись местами Пример
Свойства опрераций над матрицами A+B=B+A (A+B)+C=A+(B+C) λ(A+B)=λA+λB A(B+C)=AB+AC (A+B)C=AC+BC λ(AB)=(λA)B=A(λB) A(BC)=(AB)C (A')'=A (λA)'=λ(A)' (A+B)'=A'+B' (AB)'=B'A' 6)Ме́тод Га́усса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы. Пусть исходная система выглядит следующим образом
Матрица Тогда, согласно свойству элементарных преобразований над строками, основную матрицу этой системы можно привести к ступенчатому виду (эти же преобразования нужно применять к столбцу свободных членов):
При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных Тогда переменные Если хотя бы одно число Пусть Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом
Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают. 7) Рассмотрим проблему определения операции, обратной умножению матриц. Пусть A— квадратная матрица порядка n Матрица A−1, удовлетворяющая вместе с заданной матрицей A равенствам: A−1⋅A=A⋅A−1=E,A−1⋅A=A⋅A−1=E, называется обратной. Матрицу A называют обратимой, если для нее существует обратная, в противном случае — необратимой. Обратная матрица может существоватьтолько для квадратных матриц т.е. для тех матриц, у которых число строк и столбцов совпадают. |
|




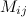 к элементу
к элементу  определителя
определителя  -го порядка называетсяопределитель
-го порядка называетсяопределитель  -го порядка, полученный из исходного вычеркиванием
-го порядка, полученный из исходного вычеркиванием  -той строки и
-той строки и  -того столбца. Задание. Найти минор
-того столбца. Задание. Найти минор  к элементу
к элементу  определителя
определителя  .
.

 к элементу
к элементу 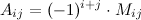
 к элементу
к элементу 

 , то система (1) является совместной и имеет единственное решение, описываемое формулой
, то система (1) является совместной и имеет единственное решение, описываемое формулой 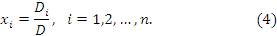
 ;
;  – определитель, полученный из определителя D заменой i-го столбца столбцом свободных членов матрицы B:
– определитель, полученный из определителя D заменой i-го столбца столбцом свободных членов матрицы B:

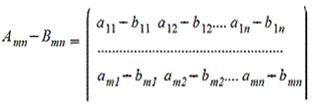







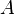 называется основной матрицей системы,
называется основной матрицей системы,  — столбцом свободных членов.
— столбцом свободных членов.
 [4].
[4]. , где
, где  , то рассматриваемая система несовместна, т.е. у неё нет ни одного решения.
, то рассматриваемая система несовместна, т.е. у неё нет ни одного решения. для любых
для любых  (
(  , где
, где  — номер строки):
— номер строки): ,
,