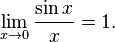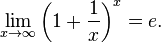Обратная связь
|
Уравнение линии в пространстве Линию в пространстве можно рассматривать как линию пересечения двух поверхностей (см. рис. 1) или как геометрическое место точек, общих двум поверхностям. Если F 1 ( x ; y ; z )=0 и F 2 ( x ; y ; z )=0 – уравнения двух поверхностей, определяющих линию L, то координаты точек этой линии удовлетворяют системе двух уравнений с тремя неизвестными:
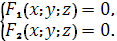
26)угол между двумя прямыми формула

27) параметрические уравнения прямой в пространстве
Мы уже выводили параметические уравнения прямой на плоскости, давайте получим параметрические уравнения прямой, которая задана в прямоугольной системе координат в трехмерном пространстве. Пусть в трехмерном пространстве зафиксирована прямоугольная система координатOxyz. Зададим в ней прямую a (смотрите раздел способы задания прямой в пространстве), указав направляющий вектор прямой  и координаты некоторой точки прямой и координаты некоторой точки прямой  . От этих данных будем отталкиваться при составлении параметрических уравнений прямой в пространстве. . От этих данных будем отталкиваться при составлении параметрических уравнений прямой в пространстве.
Пусть  - произвольная точка трехмерного пространства. Если вычесть из координат точки М соответствующие координаты точки М1, то мы получим координаты вектора - произвольная точка трехмерного пространства. Если вычесть из координат точки М соответствующие координаты точки М1, то мы получим координаты вектора  (смотрите статью нахождение координат вектора по координатам точек его конца и начала), то есть, (смотрите статью нахождение координат вектора по координатам точек его конца и начала), то есть,  . Очевидно, что множество точек . Очевидно, что множество точек  определяет прямую а тогда и только тогда, когда векторы определяет прямую а тогда и только тогда, когда векторы  и и  коллинеарны. коллинеарны.

Запишем необходимое и достаточное условие коллинеарности векторов  и и  : :  , где , где  - некоторое действительное число. Полученное уравнение называется векторно-параметрическим уравнением прямой в прямоугольной системе координат Oxyz в трехмерном пространстве. Векторно-параметрическое уравнение прямой в координатной форме имеет вид - некоторое действительное число. Полученное уравнение называется векторно-параметрическим уравнением прямой в прямоугольной системе координат Oxyz в трехмерном пространстве. Векторно-параметрическое уравнение прямой в координатной форме имеет вид  и представляет собой параметрические уравнения прямой a. Название "параметрические" не случайно, так как координаты всех точек прямой задаются с помощью параметра и представляет собой параметрические уравнения прямой a. Название "параметрические" не случайно, так как координаты всех точек прямой задаются с помощью параметра  . .
Приведем пример параметрических уравнений прямой в прямоугольной системе координат Oxyz в пространстве:  . Здесь . Здесь  . .
28) ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ
Прямые линии, принадлежащие плоскости и занимающие частное положение по отношению к плоскостям проекций, называются главными линиями плоскости.
Очевидно, что если прямая не имеет двух общих точек с плоскостью, то она или параллельна плоскости, или пересекает ее. Большое значение для задач начертательной геометрии имеет частный случай пересечения прямой и плоскости, когда прямая перпендикулярна плоскости.
Определение взаимного положения прямой и плоскости - позиционная задача, для решения которой применяетсяметод вспомогательных секущих плоскостей.
29) Числовые последовательности представляют собой бесконечные множества чисел. Примерами последовательностей могут служить: последовательность всех членов бесконечной геометрической прогрессии, последовательность приближенных значений  (x1 = 1, х2 = 1,4, х3 = 1,41, ...), последовательность периметров правильных n-угольников, вписанных в данную окружность. Уточним понятие числовой последовательности. Определение 1. Если каждому числу n из натурального ряда чисел 1, 2, 3,..., п,...поставлено в соответствие вещественное число xп, то множество вещественных чисел x1, x2, x3, …, xn, … (2.1) (x1 = 1, х2 = 1,4, х3 = 1,41, ...), последовательность периметров правильных n-угольников, вписанных в данную окружность. Уточним понятие числовой последовательности. Определение 1. Если каждому числу n из натурального ряда чисел 1, 2, 3,..., п,...поставлено в соответствие вещественное число xп, то множество вещественных чисел x1, x2, x3, …, xn, … (2.1)
30) Конечная или бесконечно удаленная точка числовой прямой называется пределом некоторой числовой последовательности действительных чисел, если какова бы ни была окрестность точки a, она содержит все члены рассматриваемой последовательности, начиная с некоторого номера.
Этот номер зависит, вообще говоря, от выбора окрестности точки a. Сформулированное условие равносильно тому, что вне любой окрестности точки a находится лишь конечное число членов рассматриваемой последовательности. Вспомнив, что окрестности конечных и бесконечно удаленных точек числовой прямой определяются заданием некоторого числа  > 0 (п. 2.2), определение предела последовательности действительных чисел можно перефразировать следующим образом. > 0 (п. 2.2), определение предела последовательности действительных чисел можно перефразировать следующим образом.
Точка a (конечная или бесконечно удаленнная) числовой прямой называется пределом последовательности {xn} действительных чисел, если для любого  > 0 существует такой номер > 0 существует такой номер  , что для всех номеров n > , что для всех номеров n >  члены xn содержатся в окрестности U(a; члены xn содержатся в окрестности U(a;  ): ):
xn 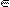 U(a; U(a;  ), n > ), n >  .
Теоремы о пределах
1. Бесконечно большие и бесконечно малые.
Функция f(x) стремится к бесконечности при x стремящимся к a, если для любого M > 0 можно указать такое значение d > 0, что для всех x удовлетворяющих неравенству |x-a| < dимеет место неравенство |f(x)| > M.
limx® a=¥
2. Функция ограниченная при x® a.
3. Функция ограниченная при x® ¥.
4. Теорема. Если limx® a f(x)=b, то функция f(x) ограниченная при x® a.
5. Бесконечно малые и их свойства. limx® a a(x)=0
Теорема. 1. Если f(x)=b+a, где a - б.м. при x® a, то limx® a f(x)=b и обратно, если limx® af(x)=b, то можно записать f(x)=b+a(x).
Теорема. 2. Если limx® a a(x)=0 и a(x) ¹ 0, то 1/a® ¥.
Теорема. 3. Сумма конечного числа б.м. есть б.м.
Теорема. 4. Произведение б.м. на ограниченную функцию есть б.м.
6. Теоремы о пределах.
Теорема. 1. Предел суммы есть сумма пределов.
Теорема. 2. Предел произведения есть произведение пределов.
Теорема. 3. Предел частного есть частное пределов (если знаменатель не обращается в 0).
Теорема. 4. Если u(x) £ z(x) £ v(x), и limx® a u(x)=limx® a v(x)=b, то limx® a z(x)=b. ("Теорема о двух милиционерах").
7. Первый замечательный предел. .
Теоремы о пределах
1. Бесконечно большие и бесконечно малые.
Функция f(x) стремится к бесконечности при x стремящимся к a, если для любого M > 0 можно указать такое значение d > 0, что для всех x удовлетворяющих неравенству |x-a| < dимеет место неравенство |f(x)| > M.
limx® a=¥
2. Функция ограниченная при x® a.
3. Функция ограниченная при x® ¥.
4. Теорема. Если limx® a f(x)=b, то функция f(x) ограниченная при x® a.
5. Бесконечно малые и их свойства. limx® a a(x)=0
Теорема. 1. Если f(x)=b+a, где a - б.м. при x® a, то limx® a f(x)=b и обратно, если limx® af(x)=b, то можно записать f(x)=b+a(x).
Теорема. 2. Если limx® a a(x)=0 и a(x) ¹ 0, то 1/a® ¥.
Теорема. 3. Сумма конечного числа б.м. есть б.м.
Теорема. 4. Произведение б.м. на ограниченную функцию есть б.м.
6. Теоремы о пределах.
Теорема. 1. Предел суммы есть сумма пределов.
Теорема. 2. Предел произведения есть произведение пределов.
Теорема. 3. Предел частного есть частное пределов (если знаменатель не обращается в 0).
Теорема. 4. Если u(x) £ z(x) £ v(x), и limx® a u(x)=limx® a v(x)=b, то limx® a z(x)=b. ("Теорема о двух милиционерах").
7. Первый замечательный предел.
| 0.5sin(x) < 0.5x < 0.5tg(x)
| |
8. Второй замечательный предел.
Переменная величина
при n® ¥ имеет предел, заключенный между 2 и 3.
· 31) Основные элементарные функции
· область определения функции;
· поведение функции на границах области определения, вертикальные асимптоты (при необходимости смотрите статью классификация точек разрыва функции);
· четность и нечетность;
· область значений функции;
· промежутки возрастания и убывания, точки экстремума;
· промежутки выпуклости (выпуклости вверх) и вогнутости (выпуклости вниз), точки перегиба (при необходимости смотрите статью выпуклость функции, направление выпуклости, точки перегиба, условия выпуклости и перегиба);
· наклонные и горизонтальные асимптоты;
· особые точки функций;
· особые свойства некоторых функций (например, наименьший положительный период у тригонометрических функций).
32)Функция одной переменной. Определение предела функции в точке по Коши.Число bназывается пределом функции у = f(x) при х, стремящемся к а (или в точке а), если для любого положительного числа e существует такое положительное число d, что при всех х ≠ а, таких, что |x – a | < d, выполняется неравенство
| f(x) – a | < e .
Определение предела функции в точке по Гейне. Число b называется пределом функции у = f(x) при х, стремящемся к а (или в точке а), если для любой последовательности {xn}, сходящейся ка (стремящейся к а, имеющей пределом число а), причем ни при каком значении n хn ≠ а, последовательность {yn = f(xn)} сходится к b.
Данные определения предполагают, что функция у = f(x) определена в некоторой окрестноститочки а, кроме, быть может, самой точки а.
Определения предела функции в точке по Коши и по Гейне эквивалентны: если число b служит пределом по одному из них, то это верно и по второму.
Указанный предел обозначается так:

Геометрически существование предела функции в точке по Коши означает, что для любого числа e > 0 можно указать на координатной плоскости такой прямоугольник с основанием 2d > 0, высотой 2e и центром в точке (а; b), что все точки графика данной функции на интервале (а–d; а + d), за исключением, быть может, точки М(а; f(а)), лежат в этом прямоугольник
· 33)Первый замечательный предел:
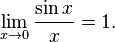
· Второй замечательный предел:
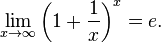
|
|
©2015- 2024 pdnr.ru Все права принадлежат авторам размещенных материалов.
|
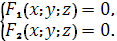

 и координаты некоторой точки прямой
и координаты некоторой точки прямой  . От этих данных будем отталкиваться при составлении параметрических уравнений прямой в пространстве.
. От этих данных будем отталкиваться при составлении параметрических уравнений прямой в пространстве. - произвольная точка трехмерного пространства. Если вычесть из координат точки М соответствующие координаты точки М1, то мы получим координаты вектора
- произвольная точка трехмерного пространства. Если вычесть из координат точки М соответствующие координаты точки М1, то мы получим координаты вектора  (смотрите статью нахождение координат вектора по координатам точек его конца и начала), то есть,
(смотрите статью нахождение координат вектора по координатам точек его конца и начала), то есть,  . Очевидно, что множество точек
. Очевидно, что множество точек  коллинеарны.
коллинеарны.
 , где
, где  - некоторое действительное число. Полученное уравнение называется векторно-параметрическим уравнением прямой в прямоугольной системе координат Oxyz в трехмерном пространстве. Векторно-параметрическое уравнение прямой в координатной форме имеет вид
- некоторое действительное число. Полученное уравнение называется векторно-параметрическим уравнением прямой в прямоугольной системе координат Oxyz в трехмерном пространстве. Векторно-параметрическое уравнение прямой в координатной форме имеет вид  и представляет собой параметрические уравнения прямой a. Название "параметрические" не случайно, так как координаты всех точек прямой задаются с помощью параметра
и представляет собой параметрические уравнения прямой a. Название "параметрические" не случайно, так как координаты всех точек прямой задаются с помощью параметра  . Здесь
. Здесь  .
. (x1 = 1, х2 = 1,4, х3 = 1,41, ...), последовательность периметров правильных n-угольников, вписанных в данную окружность. Уточним понятие числовой последовательности. Определение 1. Если каждому числу n из натурального ряда чисел 1, 2, 3,..., п,...поставлено в соответствие вещественное число xп, то множество вещественных чисел x1, x2, x3, …, xn, … (2.1)
(x1 = 1, х2 = 1,4, х3 = 1,41, ...), последовательность периметров правильных n-угольников, вписанных в данную окружность. Уточним понятие числовой последовательности. Определение 1. Если каждому числу n из натурального ряда чисел 1, 2, 3,..., п,...поставлено в соответствие вещественное число xп, то множество вещественных чисел x1, x2, x3, …, xn, … (2.1) > 0 (п. 2.2), определение предела последовательности действительных чисел можно перефразировать следующим образом.
> 0 (п. 2.2), определение предела последовательности действительных чисел можно перефразировать следующим образом.  , что для всех номеров n >
, что для всех номеров n > 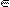 U(a;
U(a;