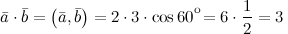|
|
Расстояние между двумя точками. Деление отрезка в данном отношенииРасстояние d между двумя точками
Координаты x, y, z точки М, которая делит отрезок
В частности, при
Уравнение прямой с угловым коэффициентом Если в общем уравнении прямой
где a – угол, образованный прямой с положительным направлением оси Однозначно определить прямую можно, задав одну точку и угловой коэффициент. А именно, уравнение прямой, проходящей через точку
Пример 1. Составить уравнение прямой проходящей через (.)А(-1,2) с угловым коэффициентом Решение. Воспользуемся формулой (2), подставив координаты данной точки и угловой коэффициент Ответ: общее уравнение прямой
Уравнение прямой на плоскости Определение.Любая прямая на плоскости может быть задана уравнением первого порядка Ах + Ву + С = 0, причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим уравнением прямой.В зависимости от значений постоянных А,В и С возможны следующие частные случаи: • C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат • А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох • В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу • В = С = 0, А ≠0 – прямая совпадает с осью Оу • А = С = 0, В ≠0 – прямая совпадает с осью Ох Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий. Уравнение прямой в отрезках – описание и пример. Пусть на плоскости зафиксирована прямоугольная декартова систему координатOxy. Уравнение прямой в отрезках на плоскости в прямоугольной системе координатOxy имеет вид Уравнение прямой в отрезках не случайно получило такое название - абсолютные величины чисел a и b равны длинам отрезков, которые отсекает прямая на координатных осях Ox и Oy, считая от начала координат. Поясним этот момент. Мы знаем, что координаты любой точки прямой удовлетворяют уравнению этой прямой. Тогда отчетливо видно, что прямая, заданная уравнением прямой в отрезках, проходит через точки
Теперь стало понятно, что уравнение прямой в отрезках позволяет легко производить построение этой прямой линии в прямоугольной системе координат Oxy. Чтобы построить прямую линию, которая задана уравнением прямой в отрезках вида Приведем пример. Пример. Постройте прямую линию, заданную уравнением прямой в отрезках вида Решение. По заданному уравнению прямой в отрезках видно, что прямая проходит через точки
Нормальное уравнение прямой Нормальное уравнение прямой имеет вид
где Нормальное уравнение можно получить из общего уравнения (1), умножив его на нормирующий множитель Косинусы углов между прямой и осями координат называют направляющими косинусами, a – угол между прямой и осью
тем самым, нормальное уравнение можно записать в виде
Расстояние от точки
Пример 5.Даны точка А(3,-1) и уравнение прямой 1) Привести уравнение к нормальному виду, найти расстояние от точки до прямой. 2) Составить уравнение прямой, проходящей через точку А параллельно данной прямой. Решение. 1) Найдем нормирующий множитель
где
Найдем по таблице угол
2) Прямая, параллельная данной, имеет тот же угловой коэффициент. По формуле (3) составим уравнение Ответ: нормальное уравнение прямой 12)Эллипсом - называется геометрическое место точек, сумма расстояний от которых до двух заданных точек F1 и F2 , называемых фокусами эллипса, есть величина постоянная.
13) Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек F1 и F2 есть величина постоянная (2a) , меньшая расстояния (2c) между этими заданными точками. Это геометрическое определение выражает фокальное свойство гиперболы. 14) Параболой называется геометрическое место точек плоскости, равноудаленных от заданной точкиF и заданной прямойd, не проходящейчерез заданную точку. Это геометрическое определение выражает директориальное свойство параболы. 15) Покажем как происходит сложение двух векторов. Сложение векторов Проиллюстрируем сложение не коллинеарных векторов на плоскости по правилу треугольника.
А на чертеже ниже показано сложение сонаправленных и противоположно направленных векторов.
Скалярным произведением двух ненулевых векторов Решение. Так как из условия
|
|
 (
(  ,
,  ,
,  ) и
) и 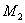 (
(  ,
,  ,
,  ) в пространстве определяется формулой
) в пространстве определяется формулой .
. , ограниченный точками
, ограниченный точками  , определяется по формулам
, определяется по формулам ,
,  ,
, 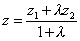 .
. имеет координаты середины данного отрезка:
имеет координаты середины данного отрезка: ,
,  ,
,  .
. , то его можно записать в виде уравнения с угловым коэффициентом
, то его можно записать в виде уравнения с угловым коэффициентом
 угловой коэффициент,
угловой коэффициент, ,
,  – свободный член, равный ординате точки пересечения прямой с осью
– свободный член, равный ординате точки пересечения прямой с осью  .
. с угловым коэффициентом
с угловым коэффициентом  , определяется по формуле
, определяется по формуле . (2)
. (2) .
. или общее уравнение
или общее уравнение  .
. и
и  заданы каноническими уравнениями
заданы каноническими уравнениями  и
и  Очевидно, угол между прямыми равен углу между направляющими векторами этих прямых:
Очевидно, угол между прямыми равен углу между направляющими векторами этих прямых:  Тогда
Тогда

 то
то 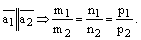
 , то
, то 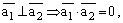 или
или 
 .
. , где a и b - некоторые отличные от нуля действительные числа.
, где a и b - некоторые отличные от нуля действительные числа.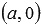 и
и 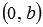 , так как
, так как 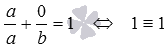 и
и  . А точки
. А точки 
 .
. . Отмечаем их и соединяем прямой линией.
. Отмечаем их и соединяем прямой линией.
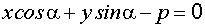 ,
, – расстояние от прямой до начала координат; a – угол между нормалью к прямой и осью
– расстояние от прямой до начала координат; a – угол между нормалью к прямой и осью  , знак mпротивоположен знаку
, знак mпротивоположен знаку  , чтобы
, чтобы  .
. ,
, .
. до прямой определяется по формуле
до прямой определяется по формуле
 .
. , m положительна, т. к.
, m положительна, т. к.  . Нормируем уравнение
. Нормируем уравнение ,
, a – угол между прямой и осью
a – угол между прямой и осью  – расстояние от прямой до начала координат.
– расстояние от прямой до начала координат. – расстояние от точки А до прямой.
– расстояние от точки А до прямой. . Уравнение можно записать
. Уравнение можно записать .
. , или в общем виде
, или в общем виде  . Вообще говоря, прямая, параллельная данной, будет иметь тот же нормальный вектор
. Вообще говоря, прямая, параллельная данной, будет иметь тот же нормальный вектор  , и её можно найти по формуле
, и её можно найти по формуле  , где
, где  – координаты точки.
– координаты точки. , где
, где  ;
; 

 и
и 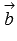 происходит так: от произвольной точки A откладывается вектор
происходит так: от произвольной точки A откладывается вектор  , равный
, равный  , равный
, равный  представляет собой сумму векторов
представляет собой сумму векторов 

 16) Если данная система векторов является базисом векторного пространства, то равенство (1) называется разложением вектора по базису . Коэффициенты линейной комбинации называются в этом случае координатами вектора относительнобазиса .
16) Если данная система векторов является базисом векторного пространства, то равенство (1) называется разложением вектора по базису . Коэффициенты линейной комбинации называются в этом случае координатами вектора относительнобазиса .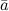 и
и  называется число, равное произведению длин этих векторов на косинус угла между ними:
называется число, равное произведению длин этих векторов на косинус угла между ними: 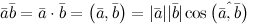 Задание. Вычислить скалярное произведение векторов
Задание. Вычислить скалярное произведение векторов  ,
,  , а
, а  , то
, то