|
|
Краткие методические указания к решению задачи 3Последовательность действий при выполнении заданий пункта 1 задачи 3 следующая: Во-первых, проводится ранжирование данных информационной таблицы по возрастанию признака Х1. Для этого составляется промежуточная табл. 5. Таблица 5
В ней значения признака Х1 располагаются по возрастанию от наименьшего к наибольшему. Соответственно вносятся в таблицу значения всех других результативных признаков. Например, если наименьшее значение признака Х1 составляет 3240, а ему соответствуют значения результативных признаков Х2 – 1650, Х3 – 5, Х4 – 0, то эти значения вносятся в первую строку промежуточной таблицы. Последующее (по возрастанию) значение признака Х1 – 4200, и соответствующие ему значения результативных признаков: Х2 – 2350, Х3 – 6, Х4 – 1 вносятся во вторую строку таблицы и т. д. Во-вторых, определяется число групп и величина интервала. Число групп определяется по формуле американского ученого Стерджесса:
K = 1 + 3,222 lg n или K = 1,44 lg n + 1,
где К – число групп; n – число единиц наблюдения. Формула Стерджесса пригодна при условии приближения распределения наблюдаемых единиц совокупности к нормальному распределению. При этом применяются равные интервалы. Величина интервала определяется по формуле I =
где Xmax, Xmin – наибольшее и наименьшее значение признака – Х1, округление до целого числа производится в большую сторону. В-третьих, образуются группы с равными интервалами по признаку Х1. Для этого к минимальному значению признака Х1, которое является нижней границей признака для первой группы, прибавляется найденное значение интервала i, т. е. Xmin+i. В результате определена верхняя граница признака для первой группы и т. д. Оформляется в виде табл. 6. Таблица 6
В-четвертых, все единицы наблюдения и соответственно значения результативных признаков распределяются в вышесказанных группах. В тех случаях, когда возникает вопрос в какую группу включать единицы наблюдения, у которых значение признака совпадает с границами интервала, следует руководствоваться принципом «включительно» или «исключительно». Например, если значение непрерывного количественного признака Х1 = Хmin+i, то данная единица наблюдения в соответствии с принципом «включительно» должна быть включена в первую очередь в первую группу. В-пятых, проводится расчет показателей по группам, согласно условию задачи, пункты а, б, в. Итоговые групповые абсолютные величины определяются простым суммированием числа единиц наблюдений и индивидуальных значений признаков – Х1, Х2, Х3 и Х4 по каждой группе в отдельности. Относительные величины, выраженные в процентах исчисляются по общим арифметическим правилам в виде пропорции
Средние величины по группам и их дисперсии определяются по уже приведенным формулам (2) и (5) задачи 2. Расчеты проводятся по каждому признаку – Х1, Х2, Х3 и Х4 и по каждой группе в отдельности. И, наконец, в-шестых, составляются выходные статистические таблицы. Ниже для иллюстрации приводятся результаты расчетов по пункту 1, подпункты а, б, в задачи 3, выполненные по данным базовой информационной таблицы. 1. Число групп и величина интервала
K = 1 + 3,222 lg 30 = 6; R = Xmax – Xmin = 12000 – 3240 = 8760;
2. Выходные статистические (табл. 7–10). Таблица 7 Число единиц наблюдения по группам (в абсолютных и относительных величинах)
Таблица 8 |
|
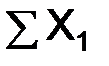
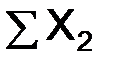
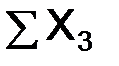
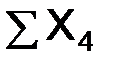
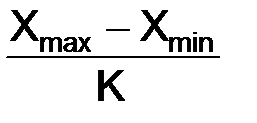 ,
, .
.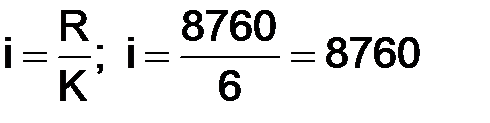 .
.