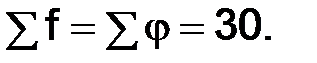|
|
Краткие методические указания к решению задачи 10Под математическим выравниванием частот эмпирического ряда в общем случае понимается замена его теоретическим рядом распределения, имеющим определенное аналитическое выражение (параметры последнего определяются по данным эмпирического ряда). В практике статистического исследования приходится встречаться с самыми различными распределениями. Наиболее распространенными является нормальное распределение. Для того чтобы построить нормальное распределение достаточно располагать двумя статистическими характеристиками – Кривая нормального распределения выражается уравнением
где В этом уравнении Например, если t = 0, то При Точечная функция затабулирована и представлена во всех учебных пособиях по теории статистики как приложение (таблица значений распределения вероятностей в случае нормального распределения). Последовательность расчета теоретических частот по формуле кривой нормального распределения сводится к следующему: 1) рассчитывается средняя арифметическая ряда 2) рассчитывается среднеквадратическое отклонение σ; 3) находится нормированное отклонение каждого варианта от средней арифметической, т. е. 4) для найденных t по табл. 26 5) рассчитывается константа 6) каждое значение Результаты умножения (после округления до целых чисел) будут искомыми частотами теоретической кривой распределения. После выравнивания ряда, т. е. исчисления теоретических частот возникает необходимость в проверке, «случайности» или «неслучайности» расхождения между эмпирическими и теоретическими частотами, и тем самым проверки правильности выдвинутой гипотезы об обоснованности нормального распределения. В этих целях рассчитываются критерии согласия: а) Пирсона Полученные результаты расчетов значение При определении нормального распределения используется 2 параметра – это Если фактическое значение б) критерий Романовского Если значение критерия Романовского меньше 3, то можно считать расхождение между эмпирическими и теоретическими частотами случайным; в) критерий Колмогорова
где d – максимальная разность между накопленными эмпирическими и теоретическими частотами; n – число единиц совокупности. При принятом уровне значимости и заданном числе степеней свободы по специальной таблице значений функции Колмогорова определяется расчетное значение критерия. Ниже представляется последовательность расчетов и их результаты (табл. 27). В расчете использованы следующие статистические характеристики: Таблица 26 Последовательность расчета теоретических частот φ
Рис. 6. Эмпирические и теоретические распределения частот
Таблица 27 |
|
 и
и  , расчеты которых неоднократно проводились в предшествующих задачах данной работы.
, расчеты которых неоднократно проводились в предшествующих задачах данной работы.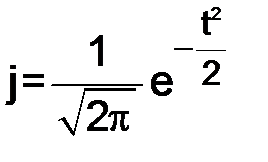 ,
,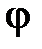 – ордината кривой нормального распределения;
– ордината кривой нормального распределения;  , e – математические константы,
, e – математические константы,  = 3,1416; e = 2,7132 – основание натурального логарифма.
= 3,1416; e = 2,7132 – основание натурального логарифма.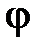 рассматривается как функция t, т. е. каждому значению t соответствует определенное значение
рассматривается как функция t, т. е. каждому значению t соответствует определенное значение 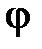 .
.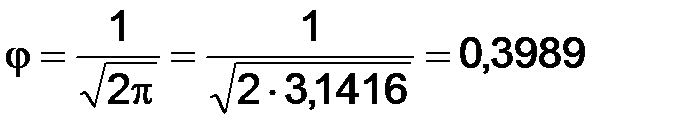 .
. = 1; при t = 1;
= 1; при t = 1; 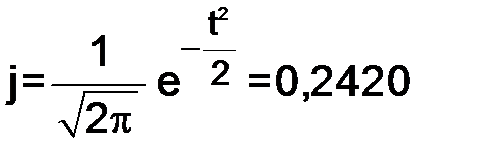 .
. ;
;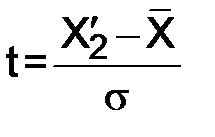 ;
;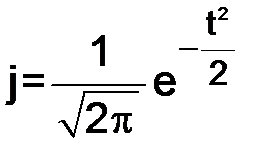 находится
находится  (теор);
(теор);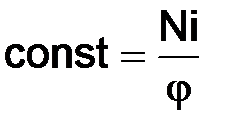 ;
;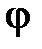 (1) умножается на константу const.
(1) умножается на константу const. , где
, где 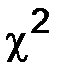 – «хи квадрат».
– «хи квадрат». сравнивается с табличным значением при принятом уровне значимости (0,10; 0,05; 0,01) к заданным числом степеней свободы. Число степеней свободы определяется как число групп в ряду распределения минус число параметров и минус единица K–n–1.
сравнивается с табличным значением при принятом уровне значимости (0,10; 0,05; 0,01) к заданным числом степеней свободы. Число степеней свободы определяется как число групп в ряду распределения минус число параметров и минус единица K–n–1. и σ, т. е., если К = 6, то число степеней свободы определяется 6 – 2 – 1 = 3.
и σ, т. е., если К = 6, то число степеней свободы определяется 6 – 2 – 1 = 3.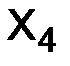 оказывается меньше табличного, то расхождение между эмпирическими и теоретическими частотами признается случайным и распределение не отвергается (рис. 6);
оказывается меньше табличного, то расхождение между эмпирическими и теоретическими частотами признается случайным и распределение не отвергается (рис. 6);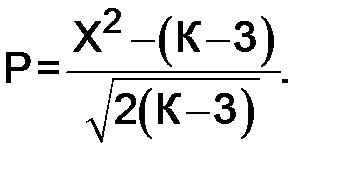
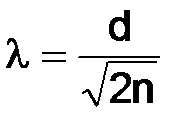 ,
, ;
; 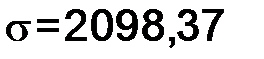 ; i = 1500.
; i = 1500.