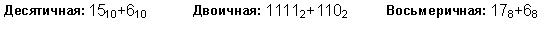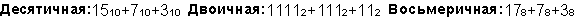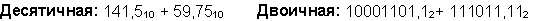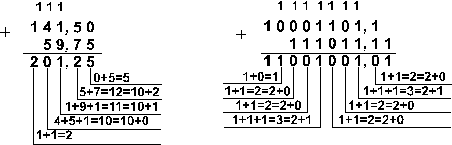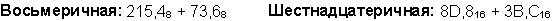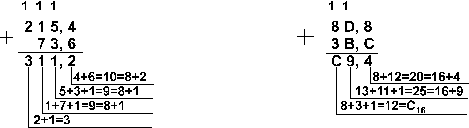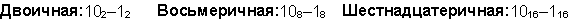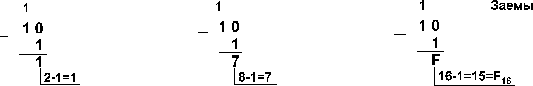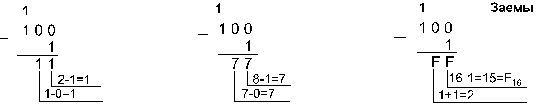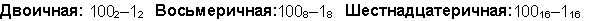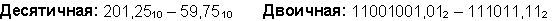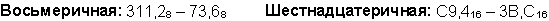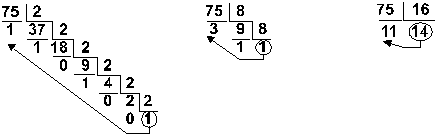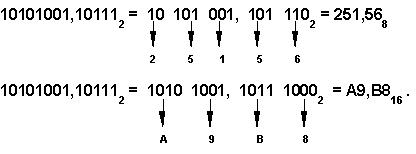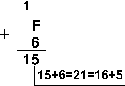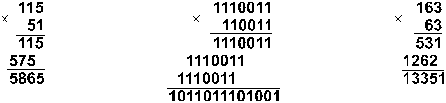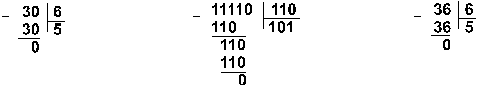Сложение в шестнадцатиричной системе

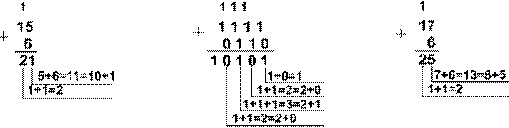
При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево.

Пример 1. Сложим числа 15 и 6 в различных системах счисления.

Шестнадцатеричная: F16+616

Ответ: 15+6 = 2110 = 101012 = 258 = 1516. Проверка. Преобразуем полученные суммы к десятичному виду: 101012 = 24 + 22 + 20 = 16+4+1=21, 258 = 2*81 + 5*80 = 16 + 5 = 21, 1516 = 1*161 + 5*160 = 16+5 = 21.

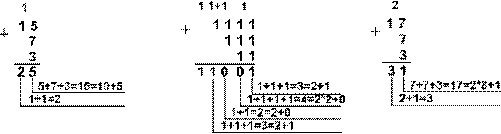
Пример 2. Сложим числа 15, 7 и 3.

Шестнадцатеричная: F16+716+316

Ответ: 5+7+3 = 2510 = 110012 = 318 = 1916. Проверка: 110012 = 24 + 23 + 20 = 16+8+1=25, 318 = 3*81 + 1*80 = 24 + 1 = 25, 1916 = 1*161 + 9*160 = 16+9 = 25.

Пример 3. Сложим числа 141,5 и 59,75.

Ответ: 141,5 + 59,75 = 201,25₁₀ = 11001001,01₂ = 311,2₈ = C9,4₁₆

Проверка. Преобразуем полученные суммы к десятичному виду:
11001001,01₂ = 2⁷ + 2⁶ + 2³ + 2⁰ + 2^-2 = 201,25
311,2₈ = 3*8² + 1•8¹ + 1*8⁰ + 2*8^-1 = 201,25
C9,4₁₆ = 12*16¹ + 9*16⁰ + 4*16^-1 = 201,25

Вычитание

Пример 4. Вычтем единицу из чисел 10₂, 10₈ и 10₁₆

Пример 5. Вычтем единицу из чисел 100₂, 100₈ и 100₁₆.

Пример 6.Вычтем число 59,75 из числа 201,25.

Ответ: 201,25₁₀ – 59,75₁₀ = 141,5₁₀ = 10001101,1₂ = 215,4₈ = 8D,8₁₆.

Проверка. Преобразуем полученные разности к десятичному виду:
10001101,1₂ = 2⁷ + 2³ + 2² + 2⁰ + 2^–1 = 141,5;
215,4₈ = 2*8² + 1*8¹ + 5*8⁰ + 4*8^–1 = 141,5;
8D,8₁₆ = 8*16¹ + D*16⁰ + 8*16^–1 = 141,5.

Пример Перевести число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

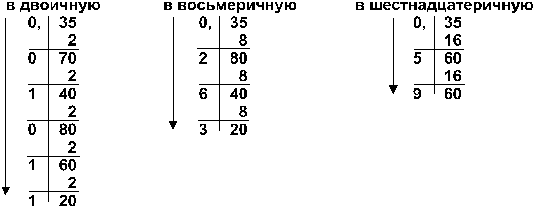
Ответ: 75₁₀ = 1 001 011₂ = 113₈ = 4B₁₆.

Правило 2 Пpи переводе правильной десятичной дpоби в систему счисления с основанием qнеобходимо сначала саму дробь, а затем дробные части всех последующих произведений последовательно умножать на q, отделяя после каждого умножения целую часть пpоизведения. Число в новой системе счисления записывается как последовательность полученных целых частей пpоизведения. Умножение пpоизводится до тех поp, пока дpобная часть пpоизведения не станет pавной нулю. Это значит, что сделан точный пеpевод. В пpотивном случае пеpевод осуществляется до заданной точности (количество знаков после запятой)

Пример Перевести число 0,35 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

Ответ: 0,35₁₀ = 0,01011₂ = 0,263₈ = 0,59₁₆.

Перевод чисел из любой системы счисления в 10 чную систему счисления

При переводе числа из любой системы счисления в десятичную надо это число представить в виде суммы степеней основания его системы счисления.

Пример

Перевод чисел из 8, 16-чной системы счисления в 2-чную систему счисления

Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).

Пример

Перевод чисел из 2-чной системы счисления в 8,16-чную систему счисления

Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.

Пример

Арифметические действия над числами в любой позиционной системе счисления

Арифметические действия над числами в любой позиционной системе счисления производятся по тем же правилам, что и в десятичной системе счисления, т.к.все они основываются на правилах выполнения действий над соответствующими полиномами.

Пример 1 Сложим числа 15 и 6 в 10-чной, 2-чной, 8-чной, 16-чной системах счисления.

Пример 2 Вычтем число 59,75 из числа 201,25 в 10-чной, 2-чной, 8-чной, 16-чной системах счисления.

Пример 3 Перемножим числа 115 и 51 в 10-чной, 2-чной, 8-чной системах счисления.

Пример 4 Разделим число 30 на число 6 в 10-чной, 2-чной, 8-чной системах счисления.

Самостоятельная работа

1. Переведите числа в десятичную систему, а затем проверьте результаты, выполнив обратные переводы:

2.Переведите числа из десятичной системы в двоичную, восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратные переводы:

а) 125₁₀; б) 229₁₀; в) 88₁₀; г) 37,25₁₀; д) 206,125₁₀.
3.Переведите числа из двоичной системы в восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратные переводы:

4.Переведите в двоичную и восьмеричную системы шестнадцатеричные числа:

а) 2СE₁₆; б) 9F40₁₆; в) ABCDE₁₆; г) 1010,101₁₆; д) 1ABC,9D₁₆.

Задания

1. Переведите числа из десятичной системы счисления в восьмеричную:

1) 0,43 2) 37,41 3) 2936 4) 481,625
Ответы: 1) 0,3341... 2) 45,32 3) 5570 4) 741,5

2. Переведите числа из десятичной системы счисления в шестнадцатеричную:

1) 0,17 2) 43,78 3) 25,25 4) 18,5
Ответы: 1) 0.2В8... 2) 2В.С7 3) 19,4 4) 12,8

3. Переведите числа из десятичной системы счисления в двоичную:

1) 40,5 2) 31,75 3) 124,25
Ответы:1) 101000,1 2) 11111,11 3) 1111100,01

4 . Переведите двоичные числа в восьмеричную систему счисления:

1) 1010,00100101 2) 1110,01010001 3) 1000,1111001
Ответы: 1) 12,112 2) 16,242 3) 10,744

5.Переведите двоичные числа в шестнадцатеричную

1) 1010,00100101 2) 1110,01010001 3) 100,1111001
Ответы: 1) А,25 2) Е,51 3) 4,F2

6. Переведите восьмеричные и шестнадцатеричные числа в двоичную систему счисления:

1) 266₈ 2) 1270₈ 3) 10,23₈ 4) 266₁₆ 5) 2А19₁₆ 6) 10,23₁₆
Ответы:1) 10110110 2) 1010111000 3) 1000,010011
4) 101111110110 5) 10101000011001 6) 10000,00100011