|
|
Занятие 4. Работа и энергия. Коэффициент полезного действия.Краткие теоретические сведения Основные формулы Работа, совершаемая силой
где Работа, совершаемая переменной силой:
Средняя мощность
Мгновенная мощность
Мощность при равномерном движении:
Кинетическая энергия материальной точки:
Потенциальная энергия материальной точки, находящейся в гравитационном поле Земли:
Потенциальная энергия сжатой (или растянутой) пружины
Закон сохранения импульса для замкнутых систем
Закон сохранения энергии для замкнутых систем:
Работа силы тяжести всегда направлена вертикально вниз, к Земле, и не зависит от траектории движения тела, а определяется только разностью высот начального и конечного положения тела:
Работа силы тяжести не зависит от траектории движения и на любой замкнутой траектории равна нулю. Работа силы упругости:
где Коэффициент полезного действия (КПД) механизмов:
где Вопросы для ответа у доски 1. Работа силы. Мощность. Дайте определение работы постоянной силы при прямолинейном движении. Обобщите это понятие на случай произвольной силы при криволинейном движении. Введите единицы измерения работы и дайте им определение. Получите выражение для мощности и дайте определение единицы измерения мощности. 2. Кинетическая энергия. Получите выражение для кинетической энергии материальной точки. Установите связь между работой силы, действующей на точку, и изменением кинетической энергии этой точки. 3. Потенциальная энергия. Введите понятие силового поля и дайте определение консервативных и неконсервативных сил. Найдите работу при перемещении тела в поле консервативных сил. Вычислите потенциальную энергию тела, поднятого над землей, и упруго деформированного тела. 4. Закон сохранения энергии в консервативной и неконсервативной системах. Исходя из второго закона Ньютона, получите выражение для изменения энергии системы материальных точек, на которую, кроме внутренних сил, действуют внешние консервативные и неконсервативные силы. Сформулируйте закон сохранения энергии в наиболее общем виде. Получите закон сохранения механической энергии для изолированной системы и отметьте ограниченный характер действия этого закона. Приведите примеры. Примеры решения задач: Задача 1. Автомобиль массой 2 т трогается с места и идет в гору, наклон которой составляет 0,1. Пройдя расстояние 100 м, он достиг скорости 10 м/с. Определить, мощность, развиваемую на всём пути и максимальную мощность двигателя автомобиля при разгоне, если коэффициент трения 0,05. Движение равноускоренное.
1. Определим, какую мощность требуется найти: а) Средняя мощность – это мощность, развиваемая на всем пути:
б) Максимальная мощность – это мгновенная мощность:
где Так как
2. Найдем силу тяги ( Запишем для этого II закон Ньютона в векторном виде:
Выбираем оси для проецирования (оси удобно выбрать так: одну – по ускорению, другую – ей перпендикулярную) и спроецируем на них вектора, входящие в уравнение. Получим:
Сила тяги из проекции на ось
Сила реакции опоры из проекции на ось
Сила трения:
Подставив выражения для силы трения в выражение для силы тяги, получим:
где ускорение движения автомобиля:
3. Определим среднюю скорость при равноускоренном движении автомобиля:
После подстановки числовых значений величин, получим:
4. Так как сила тяги
Ответ: Задача 2. Какую работу надо совершить, чтобы стальной стержень, лежащий на столе, приподнять за один конец так, чтобы стержень составил угол 300 с поверхностью стола. Сечение стержня 2см2, длина 0,5м, плотность стали 8·103кг/м3.

1 состояние: стержень в горизонтальном положении покоится на столе.
2 состояние: стержень покоится под углом 300 к горизонту:
где Тогда Масса стержня: Подставив в (1) выражение массы стержня, получим: Вычисляя, находим: Ответ: Задача 3. Тело, брошенное с высоты 250 м вертикально вниз со скоростью 20м/с, погрузилось в грунт на глубину 20 см. Найти среднюю силу сопротивления грунта, если масса тела 2 кг. Сопротивлением воздуха пренебречь.
1) телу сообщена начальная скорость на высоте (
2) тело остановилось в грунте: Тогда,
Так как
Подставив числовые значения, получим: Ответ: Вопросы и задания для самопроверки: 1. Приведите примеры совершения положительной и отрицательной работы. 2. Разъясните физический смысл понятий работы и энергии. 3. Совершает ли работу неподвижно стоящий человек, если он держит в руке груз, например ведро с водой? 4. Пассажир давит на переднюю стенку вагона с силой 5. Какой критерий консервативности сил вы знаете? 6. В чем состоит особенность работы силы тяжести и силы упругости? 7. На полу лежат куб и шар, сделанные из одинакового материала и имеющие одинаковые массы. Их поднимают до соприкосновения с потолком. Одинаково ли изменяется при этом их потенциальная энергия? 8. Цилиндр и куб из одинакового материала, одинаковой высоты и массы стоят на горизонтальной плоскости. Какое из этих двух тел труднее опрокинуть? 9. Может ли кинетическая энергия тела быть больше его полной энергии? 10. Что такое внутренняя энергия тела? 11. Что означает термин “рассеяние энергии”? 12. Две одинаковые пружины (железная и медная) растянуты на одинаковую длину. На растяжение которой из них надо затратить большую работу? 13. Две одинаковые пружины (железная и медная) упруго растянуты одинаковыми силами. На растяжение, которой из них надо затратить большую работу? 14. Начертите графики зависимости потенциальной и кинетической энергии шарика массой 15. Человек поднимается по эскалатору метрополитена. В каком случае электродвигатель будет развивать большую мощность: когда человек идет равномерно по лестнице вверх или когда стоит? В каком случае электродвигатель производит большую работу: когда человек стоит неподвижно или когда идет по лестнице вверх? 16. Дайте определение мгновенной и средней мощности. Задачи для самостоятельного решения: 1. С какой скоростью двигался вагон массой 20 т, если при ударе о стенку каждый буфер сжался на 10 см? Известно, что пружина каждого сжимается на 1 см под действием силы 104 Н. 2. К стальной проволоке длиной 10 м и диаметром 2 мм подвешивают груз массой 100 кг. Найти изменение объема проволоки и энергию упругой деформации. Модуль Юнга 1,96·1011 Н/м2, коэффициент Пуассона 0,3. 3. Под действием постоянной силы F вагонетка прошла путь S=5м и приобрела скорость 4. Трактор за время t=8 час вспахивает поле площадью S=2 га при захвате лемехов l=1,2 м и сопротивлении почвы Fтр=17640 Н. Определить N мощность двигателя трактора, если его коэффициент полезного действия 5. Определить мощность электродвигателя, если его якорь вращается с частотой n=2,5 с-1, а момент силы равен М=14 H·м. 6. Совершив работу, равную А=20 Дж, удаётся сжать пружину на 2 см. Определить работу, которую надо выполнить, чтобы сжать пружину на 4 см. 7. Груз массой m=5 кг падает с высоты Н=5 м и проникает в грунт на глубину L=5 см. Определить среднюю силу сопротивления грунта. 8. Для подъёма зерна на высоту Н=10 м установили транспортёр мощностью N=4 кВ. Определить массу зерна, поднятого за время t=8 час работы транспортёра. Коэффициент полезного действия установки принять равным 9. Тело массой m1=0,5 кг надает с некоторой высоты на плиту массой m2=1кг, укреплённую па пружине жёсткостью 10. Шар массой m1=2 кг, движущийся со скоростью 11. Баба копра массой m1=500 кг падает на сваю массой m2=100 кг со скоростью 1) Кинетическую энергию W1 копра в момент удара. 2) Энергию W2, затрачиваемую на деформацию сваи. 3) Энергию W3, затрачиваемую на углубление сваи в грунт. 4) Коэффициент полезного действия 12. Спутник массой m=3 т вращается вокруг Земли по круговой орбите на высоте h=520 км. Определить полную механическую энергию спутника относительно Земли. 13. Определить механическую энергию, которой обладает Луна, вращаясь в гравитационном поле Земли. 14. Спортсмен метает диск диаметром d=22 см и массой m=2 кг под углом 45° к линии горизонта с начальной скоростью 15. Вычислить, какая энергия выделится, если период вращения Земли увеличится вдвое. Масса Земли М=5,98·1024 кг, радиус Земли R=6370 км. 16. Пуля массой m1=10 г, летевшая со скоростью 17. Молот массой m1=5 кг ударяет небольшой кусок железа, лежащий на наковальне. Масса m2 наковальни равна 100 кг. Массой куска железа пренебречь. Удар неупругий. Определить КПД удара молота при данных условиях. 18. Вертолёт массой m=3 т висит в воздухе. Определить мощность N, расходуемую на поддержание вертолёта в этом положении, при двух значениях диаметра d ротора: 1) 18м; 2) 8м. При расчёте принять, что ротор отбрасывает вниз цилиндрическую струю воздуха диаметром, равным диаметру ротора. 19. При перемещении груза массой 3 т по горизонтальному пути на расстояние 300 м совершена работа 90000 Дж. Определить коэффициент трения. 20. Из шахты глубиной 200 м поднимается груз 0,5 т при помощи каната, наматываемого на барабан подъемника. Какую работу совершает подъемник при поднятии груза, если каждый метр каната имеет массу 2,5 кг. 21. Лифт, имеющий массу с грузом 500 кг, поднимается на высоту 30 м за 40с. Определить полезную мощность, развиваемую электромотором. 22. Тело массой 50 кг падает с высоты 15 м. Определить величину потенциальной и кинетической энергии на расстоянии 6 м от поверхности Земли. 23. Масса поезда в 200 раз больше массы самолета, а скорость поезда в 15 раз меньше скорости самолета. Какое из тел – самолет или поезд – обладает большей кинетической энергией и во сколько раз? 24. Пуля массой 10 г подлетает к доске со скоростью 600 м/с и, пробив ее в центре, вылетает со скоростью 400 м/с. Определить, какая часть потерянной кинетической энергии пули пошла на кинетическую энергию доски и какая выделилась в виде тепла. Масса доски равна 1 кг. 25. На тонкой нити подвешен шарик массой 100 г. Прочность нити (максимальный вес, который она может выдержать) 1,96 Н. Определить, на какой минимальный угол нужно отклонить нить от вертикали, чтобы после того, как шарик будет отпущен, нить оборвалась при прохождении шарика через положение равновесия. 26. Конькобежец, разогнавшись до скорости 25,6 км/ч, въезжает на ледяную гору. На какую высоту от начального уровня въедет конькобежец с разгона, если подъем горы составляет 0,5 м на каждые 10 м по горизонтали и коэффициент трения коньков о лед равен 0,02? 27. Канат массой 15 кг связан своими концами и переброшен через подвижный блок. Обезьяна массой 12 кг прыгает на веревку и начинает карабкаться вверх. Некоторое время она находится на одной и той же высоте. Сколько времени она сможет продержаться на этой высоте, если максимальная мощность, развиваемая обезьяной, 360 Вт? 28. Прямой тонкий стержень постоянного поперечного сечения длинной l и массой m лежит горизонтально на земле. Какую работу А нужно совершить, чтобы поставить его вертикально? 29. Какую минимальную работу А нужно совершить, чтобы поднять тело массой m на вершину горки, длина основания которой l, а высота h? Сила F направлена вдоль наклонной плоскости, коэффициент трения между плоскостью и телом 30. Ящик массой 100 кг тянут по горизонтальной плоскости с помощью веревки, наклоненной под углом 31. Тело массой m=1 кг падает с высоты h=10 м без начальной скорости. Какую мощность N будут развивать силы тяжести в момент перед ударом тела о землю? 32. Пружина игрушечного пистолета имеет жесткость k. Какую скорость 33. Груз массой m=103 кг опускается с помощью лебедки с постоянной скоростью |
|
 направленной под углом
направленной под углом  к горизонту
к горизонту
 перемещение материальной точки под действием силы,
перемещение материальной точки под действием силы,  угол между векторами силы и перемещения.
угол между векторами силы и перемещения.



 где
где  импульс.
импульс. где
где  высота подъема.
высота подъема. где
где 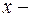 изменение размеров тела.
изменение размеров тела. .
.


 коэффициент жёсткости пружины,
коэффициент жёсткости пружины, 
 полезная работа;
полезная работа; 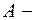 затраченная работа;
затраченная работа;  полезная мощность,
полезная мощность,  полная мощность.
полная мощность.
 ,
,
 угол между вектором силы тяги
угол между вектором силы тяги  и вектором скорости
и вектором скорости  .
. 0, то
0, то и
и  .
.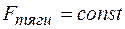 ), которая развивает эти мощности.
), которая развивает эти мощности.

 0.
0.





 ,
, ,
,
 .
.
 .
. Вт=20 кВт.
Вт=20 кВт. будет максимальная мощность:
будет максимальная мощность: ,
, 2·20 кВт=40 кВт.
2·20 кВт=40 кВт. 20 кВт,
20 кВт,  ) и не замкнутая, т.к. на стержень действует внешняя сила, которая и совершает работу по подъёму стержня.
Работа внешних сил равна изменению
) и не замкнутая, т.к. на стержень действует внешняя сила, которая и совершает работу по подъёму стержня.
Работа внешних сил равна изменению





 Найти:
Найти: 
 0.
0.
 , а другой совсем не поднимают).
, а другой совсем не поднимают). (1)
(1)
 .
. Дж=1Дж.
Дж=1Дж.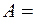 1 Дж.
1 Дж.
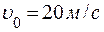

 Выберем 0-уровень потенциальной энергии на глубине х. Опишем энергию тела в двух состояниях:
Выберем 0-уровень потенциальной энергии на глубине х. Опишем энергию тела в двух состояниях: )над 0-уровнем:
)над 0-уровнем:
 0, тело покоится на 0-уровне, следовательно, кинетическая и потенциальная его энергия равна нулю.
0, тело покоится на 0-уровне, следовательно, кинетическая и потенциальная его энергия равна нулю.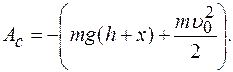
 , сила сопротивления направлена против движения, то:
, сила сопротивления направлена против движения, то:


 26,9 кН.
26,9 кН. . Совершает ли он при этом работу?
. Совершает ли он при этом работу? ,брошенного вертикально вверх с начальной скоростью
,брошенного вертикально вверх с начальной скоростью 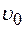 ,в зависимости от высоты подъема и от времени движения.
,в зависимости от высоты подъема и от времени движения.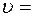 2 м/с. Определить работу А силы, если масса вагонетки m=400 кг и коэффициент трения
2 м/с. Определить работу А силы, если масса вагонетки m=400 кг и коэффициент трения 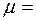 0,01.
0,01. 80%.
80%.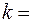 4 кН/м. Определить, на какую длину сожмётся пружина, если в момент удара скорость грузи
4 кН/м. Определить, на какую длину сожмётся пружина, если в момент удара скорость грузи 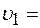 1,2 м/с, налетает на покоящийся шар массой m2=1,5 кг. Вычислить скорости шаров после упругого взаимодействия.
1,2 м/с, налетает на покоящийся шар массой m2=1,5 кг. Вычислить скорости шаров после упругого взаимодействия. удара копра о сваю.
удара копра о сваю. .
. 800 к горизонту. Коэффициент трения между ящиком и полом
800 к горизонту. Коэффициент трения между ящиком и полом  приобретает шарик массой m при стрельбе в горизонтальном направлении, если перед выстрелом пружина сжата на
приобретает шарик массой m при стрельбе в горизонтальном направлении, если перед выстрелом пружина сжата на  ?
?