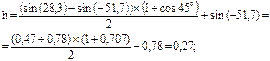|
|
Исходные данные и результаты расчета высоты Солнца
Сопоставляя полученные данные с рассчитанными ранее, а так же имеющимися в литературе, можно заключить, что зависимости (84) и (85) верны. Указанные величины позволяют определить высоту солнца в полночь и полдень, а так же определить точки его восхода и заката. Они будут на пересечении линий горизонта и линии, соединяющей Солнце в двух противоположных точках. Однако, всего этого не достаточно для определения траектории Солнца. Здесь необходимо знать высоту Солнца не только в полдень (полночь), но и любое время суток. Для решения задачи возьмем произвольную широту, пусть это будет лето, и изобразим некоторую экспозицию (рисунок 52).
Рисунок 52 – Схема к расчету высоты Солнца
На рисунке изображена траектория движения Солнца в один из летних месяцев в северном полушарии. Признаки: Солнце в полдень сориентировано точно на юг по отношению к наблюдателю Т, восходит в точке В (восход) слева, если смотреть на юг, и заходит на западе справа. Определим высоту Солнца в полдень H1 и условную высоту солнца Н2 в полночь, зная соответствующие высоты солнца h0 и h·, и приняв радиус полусферы Rп равным 1. Тогда:
Подставляя в полученные выражения значения h0 и h· из зависимостей (60) и (61) получим:
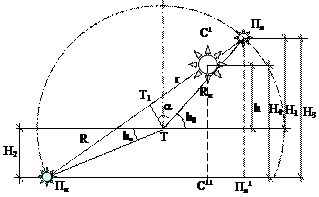
Плоскость, в которой вращается Солнце, как бы поднята над плоскостью горизонта, а ее центр Т является центром основания конуса с вершиной в точке Т. Образующей этого конуса является радиус полусферы единичного радиуса. При этом телесный угол у вершины конуса зависит от угла q, то есть от времени года. С изменением широты, конус будет поворачиваться вокруг точки Т меридиальной плоскости, оставаясь неизменным. Для большей наглядности разрежем экспозицию меридиальной плоскостью (меридиальная плоскость проходит по линии север – юг), как показано на рисунке 53.
Рисунок 53 – Схема к расчету траектории Солнца
Так как основанием конуса является окружность с радиусом R, причем солнце делает полный оборот по ней ровно за 24 часа с постоянной скоростью, то ее можно разбить на часовые секторы с началом отсчета от точки ПН (полночь – 0 часов). В момент полудня (12 часов), т.е. пройдя половину круга, солнце достигает наибольшей высоты. Но так как общепринято отсчитывать азимут от южного направления за часовой стрелкой, то и мы будем придерживаться этого правила, то есть угол А° будем отсчитывать за часовой стрелкой. Зная радиус основания конуса и угол А° найдем проекцию r линии, соединяющей точки Т1 и С (см. рисунок 70), на линию пересечения меридиальной плоскости и основания конуса:
Подставив значение r, получим:
Справедлива пропорция:
Подставляя в выражение (89) значение r из (85), и учитывая, что Н3=Н1-Н2 найдем:
С учетом выражения (89) и зная, что h=H4–H2 , получим:
По зависимости (93) можно рассчитать высоту солнца над горизонтом для любого времени суток и периода года. Для определения угловой высоты Солнца можно воспользоваться зависимостью:
Примеры. 1. Определить высоту стояния Солнца в 12 часов дня на экваторе в период летнего солнцестояния. Решение: Определим параметры, входящие в выражение (94). Угол q определим по выражению (69) или по графику (см. рисунок 69). q = 113,5°. Широта экватора Ш = 0. Для времени 12 часов угол А0 = 0. Подставляя полученные значения в выражение (94) получим:
2. Определить высоту стояния Солнца в 0 часов ночи на экваторе в период летнего солнцестояния. Решение: см. пример 1. q = 113,5°; Ш = 0°; А0 = 180°. Подставляя полученные значения в выражение (94) получим:
3. Определить высоту стояния Солнца в 18 часов дня на широте экватора в период летнего солнцестояния. Решение: см. пример 1. q = 113,5°; Ш = 0°; А0 = 90°. Подставляя полученные значения в выражение (94) получим:
4. Определить высоту стояния Солнца в полдень на Северном полюсе в период летнего солнцестояния. Решение: см. пример 1 и 2. q = 113,5°; Ш = 90°; А0 = 0°. Подставляя полученные значения в выражение (94) получим:
5. Определить высоту стояния Солнца в полночь на Северном полюсе в период летнего солнцестояния. Решение: см. приведенные выше примеры. q = 113,5°; Ш = 90°; А0 = 180°. Подставляя полученные значения в выражение (94) получим:
6. Определить высоту стояния Солнца в 6 часов утра на Северном полюсе в период летнего солнцестояния. Решение: см. приведенные выше примеры. q = 113,5°; Ш = 90°; А0 = 180°. Подставляя полученные значения в выражение (94) получим:
7. Определить время восхода и захода солнца в период летнего солнцестояния в городе Харькове. Решение: q = 113,5°; Ш = 50°. Время восхода и захода солнца будет при h = 0. Подставляя полученные значения в выражение (94) получим:
Для того, чтобы Солнце от наиболее высокой точки в полдень опустилось до горизонта, оно должно сместиться по отношению к точке Т1 на угол А°, то есть на 119,5°. Известно, что за 1 час Солнце смещается по отношению к точке Т на 15°. С учетом этого определим величину угла в часах:
Это значит, что солнце от полудня до заката пройдет 7,98 часа, следовательно, закат наступит в 12 + 7,98 = 19,98 часа = 19 ч. 59 мин. Известно, что полудуги, которые описывает Солнце от восхода до заката, и от полудня до заката, симметричны. Тогда восход Солнца наступит в 12 - 7,98 = 4,02 часа = 4 ч. 1 мин. Не следует путать полученное местное время с принятым поясным московским. 8. Определить время восхода и заката солнца в период летнего солнцестояния в городе Москве. Решение: по аналоги с задачей 7 определим А° = 128,12°. Следовательно, от полудня до заката пройдет 8,54часа. Тогда восход в Москве наступит в 12 - 8,54 = 3,48 часа = 3 ч. 29 мин. Закат наступит соответственно в 12 + 8,54 = 20,54 часа = 20 ч. 54 мин. Сопоставив примеры 7 и 8, увидим, что восход солнца в г. Харьков будет на 32 минуты запаздывать по сравнению с восходом в Москве, не смотря на то, что оба города находятся в одном часовом поясе и, более того, почти на одном меридиане. В этой связи следует подчеркнуть, что когда мы рассуждали о местном времени, то их не следовало смешивать с восходом и закатом солнца, так как они зависят не только от меридиана, но и от широты. 9. Определить, на какой высоте будет находится солнце в г. Харькове в 15 часов 20 февраля (год не високосный). Решение: Определим угол q из зависимости (94):
Зная, что год имеет 365 дней (не високосный), а угол b за год изменяется от 0° (летнее солнцестояние – 22 июня) до 360°, то за одни сутки земля сместиться от некоторого положения на:
Посчитаем теперь, сколько дней пройдет от 22 июня (за начало отсчета берем начало суток) до 20 февраля. Общее количество дней будет равно 242. Тогда угол b будет равен:
Определим q:
Теперь мы знаем уже два параметра: угол q и широту г. Харькова. Найдем третий параметр: угол А° по графику (см. рисунок 69). В 15 часов он будет составлять 45°. Подставим полученные данные в выражение (68) и найдем h.
Или в угловой мере:
|
|

 1
1


 2
2
 3
3
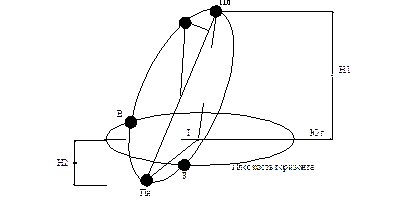
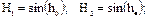 (87)
(87) (88)
(88)
 (89)
(89) (90)
(90) (91)
(91)
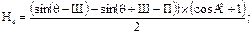 (92)
(92) (93)
(93) (94)
(94)
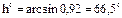
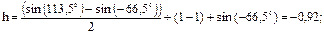









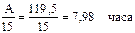


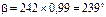
 =78,3°
=78,3°