|
|
Тема: Аналітична геометрія . Векторна алгебра.Міністерство освіти і науки України Сосницький сільськогосподарський технікум
ЗБІРНИК ПРАКТИЧНИХ ЗАВДАНЬ З ВИЩОЇ МАТЕМАТИКИ
За редакцією В. М. Пуда
Сосниця 2016
Міністерство освіти і науки України Сосницький сільськогосподарський технікум бухгалтерського обліку
Збірник практичних завдань з вищої математики
За редакцією В. М. Пуда
Сосниця 2016
Укладач: В. М. Пуд – викладач математики ССТБО
Рецензенти: О. М. Ляшок – викладач фізики та математики ССТБО
ЗАВДАННЯ Для самостійної роботи з курсу «Вища математика» для студентів ІІ курсу: 5.03050901 “Бухгалтерський облік“ 5.03050401 “Економіка підприємства“
Розглянуто та затверджено на засіданні ц/к природознавчих та фізико-математичних дисциплін Протокол № від 2016 року Голова ц/к Логвін Н.П.
Загальні методичні рекомендації Успішна реалізація досягнень науково-технічного прогресу та вирішення завдань, які ставить ринкова економіка, тісно пов’язані з використанням математичних методів та моделей при вирішенні багатьох проблем із різноманітних областей людської діяльності. Особливо важливого значення набуває використання математичних методів і засобів обчислювальної техніки в умовах ринкової економіки при розв’язанні економічних задач. У зв’язку з цим для студентів необхідні як знання можливостей застосування математичних методів та моделей у практичній діяльності, так і розуміння необхідності їх використання. Завдання для практичних занять розроблено відповідно до програми рекомендованої Міністерством освіти і науки України для студентів економічних спеціальностей навчальних закладів I - II рівнів акредитації і включають практичні завдання по таких темах: « Елементи лінійної алгебри», « Аналітична геометрія. Векторна алгебра»,» Вступ до математичного аналізу», « Диференціальне числення функції однієї змінної», «Диференціальне числення функції багатьох змінних», «Інтегральне числення та диференціальні рівняння», «Числові та степеневі ряди». Після вирішення завдань, зазначених у даному посібнику, у повному обсязі студенти зможуть:
Тема1. Елементи лінійної алгебри. Практичне заняття 1.1. Тема: Матриці, дії з ними. Мета:Засвоїти поняття: матриця, елементи матриці, розмір матриці, протилежні матриці, транспоновані матриці. Ознайомитись з різновидами матриць, із сферами їх застосування. Набути навичок виконувати найпростіші дії з матрицями: множення на число, додавання та віднімання, множення матриць
Завдання 1.Знайти добуток матриць АВ або ВА. а) А= (4 3 -2), В= б) А=
г) А= д) А= Завдання 2. Задамо матриці. А= Виконати дії. а) А*В-С*ДТ; б) А*РТ+5А-Д
Завдання 3.За допомогою елементарних перетвореньматриці знайти ранги матриць: А=
Завдання 4. Знайти обернені матриці за заданими двома способами: а) за допомогою формули алгебраїчних доповнень; б) за допомогою елементарних перетворень матриць: А=
Практичне заняття 1.2. Тема: Визначники другого, третього порядків. Мета:Засвоїти поняття визначника матриці. Набути навичок обчислення визначників другого, третього та вищих порядків. Дослідити властивості визначників. Закріпити вміння виконувати елементарні перетворення матриці.
Завдання 1. Обчислити визначник другого порядку матриці:
1) 4. Завдання 2. Обчислити визначники третього порядку.
1)
Завдання 3.Обчислити визначники четвертого порядку використовуючи формулу розкладу визначника за елементами рядка та стовпця.
1) 4) Практичне заняття 1.3. Тема: Розв’язання неоднорідних систем лінійних алгебраїчних рівнянь методами Крамера, матричним методом, методом Гаусса, Гауса-Жордана з використанням розрахункових таблиць. Мета:Дати практику розв’язання систем лінійних алгебраїчних рівнянь методом Крамера та матричним методом; закріпити навички обчислення визначників третього порядку та знаходження обернених матриць за формулою алгебраїчних доповнень та з використанням елементарних перетворень матриці Завдання 1. Розв’язати системи рівнянь методом Крамера, та матричним методом.
1) 7) 9)
Завдання 2. Розв’язати системи рівнянь методом Гаусса та Гаусса-Жордана.
1) 7)
Тема: Аналітична геометрія . Векторна алгебра. Практичне заняття 2.1.1 Тема:Вектори. Дії над вектори. Мета: Засвоїти поняття: вектор, векторний простір, лінійна залежність та лінійна незалежність векторів, базис векторного простору. Навчитись виконувати дії з векторами, обчислювати довжину вектора, кут між векторами, напрямні косинуси вектора, скалярний добуток векторів. Дати практику розкладу вектора за базисом. Завдання 1. Дано вектори
Завдання 2. Знайти довжину вектора: 1) 3)
Завдання 3.Обчисліть кут між векторами
Завдання 4.Обчисліть периметр трикутника, вершинами якого є точки: 1) А ( 4;0), В( 7;4) і С(-4;6); 2) А(6;7), В(3;3) і С(1;-5)
Завдання 5.а) Точка С ділить відрізок АВ у відношенні 3:5(від А до В). Кінець відрізка - точки А(2;3) і В(10;11). Знайти точку С. б) відрізок, кінцями якого є точки А(-5;-2), В(4;2,5), поділений у відношенні 3:4:2 (від А до В). Знайти точки поділу. в) відрізок задано точками А(-4;7), В(-3;5). Знайдіть на відрізку АВ таку точку С, щоб
Практичне завдання 2.1.2 Тема:Рівняння прямої на площині та в просторі. Мета: Ознайомитись з різновидами рівняння прямої на площині. Дослідити умови паралельності та перпендикулярності прямих, заданих загальними рівняннями та рівняннями з кутовим коефіцієнтом. Навчитись знаходити кут між прямими, відстань від заданої точки до прямої, відстань між двома точками, обчислювати площу трикутника за координатами трьох вершин. Навчитись записувати рівнянням прямої, яка проходить через дві точки; прямої, що проходить через задану точку паралельно чи перпендикулярно вектору.
Завдання 1. а)Складіть рівняння прямої, яка проходить через дану точку Мо і перпендикулярна до даного вектора б) Написати рівняння прямої, яка проходить через точки: 1) А(-1;3), В(4;-2); 2) А(5;-2), В(-3;-1); 3)А(1;-4), В(0;-6); 4) А(5;0), В(-4;-2). Завдання 2.Написати рівняння прямої, яка проходить через точку А(2,3) і утворює з віссю Ох кут: 1) 300; 2) 450; 3) 600; 4) 00 Завдання 3. Знайдіть кут між прямими: 1) у=2х+3 та у=-3х+2 2) у=-2х+3 та у=3х+5 3) у= 2х-3 та у= Завдання 4. Визначити паралельність та перпендикулярність прямих: 1) 3х-5у+7=0; 10х-30у-11=0 2) 3х-5у+7=0; 10х+6у-3=0. Завдання 5. Задані вершини трикутника. Знайти : 1) рівняння сторони ВС; 2) рівняння висоти АД; 3) рівняння медіани СЕ; 4) довжину висоти АД; 5) величину кута А; 6) площу трикутника АВС. Зробити відповідний малюнок 1)А(2;-3), В(3;2), С(-2;5); 2)А(-3;2), В(5;-2), С(1;3); 3)А(1;1), В(3;2), С(2;4);
Завдання 6. Рівняння прямої і площини у просторі. а) обчислити гострий кут між двома прямими (х-1)/3=(у+4)/-2=(7-2)/4; (х+3)/2=(у-1)3=(7=1)/-2; б) знайти точку перетину прямих: (х+3)/2=(у-1)/3=(7+5)/2 та 2х+3у+7-22=0 в)складіть рівняння прямої, яка проходить через точку Мо(-4;-3;-1) і паралельна векторам г)знайдіть відстань від точки А(1;-2;1) до площини 10х-2у+11z-10=0 д)складіть параметричне рівняння прямої, що проходить через точки координат і точку М (1;4;-3).
Завдання 7. Знайдіть відстань:1) від точки М(-2;4) до прямої 4х -3у-5=0; 2) від точки(4,6) до прямої 3х+4у+14 = 0. Завдання 8.Знайдіть відстань між двома паралельними прямими: 1) 4х+3у+33=0 і 4х+3у-17=0 2) 12х + 5у – 101 = 0 і 12х + 5у + 68 = 0 Завдання 9. Складіть рівняння прямої, яка: 1) проходить через точку перетину прямих х + у -4 = 0 і х – у = 0 паралельно прямій х – 4у + 4 = 0; 2) проходить через точку перетину прямих х/6 + у/3 = 1 і х/3 + у/6 = 1 паралельно прямій х – 2у – 6 = 0 Завдання 10.Складіть рівняння прямої, що проходить через точку перетину прямих х + 2у + 4 = 0 і 3х – у – 9 = 0 перпендикулярно до прямої х + у – 7 = 0. Практичне заняття 2.2. Тема: Криві лінії другого порядку. Мета: Дослідити властивості кривих ліній другого порядку на площині: кола, еліпса, гіперболи, параболи. Дати практику побудови даних кривих. Навчитись зводити загальні рівняння кривих ліній другого порядку до одного з канонічних рівнянь шляхом виділення повних квадратів.
Завдання 1. Скласти рівняння кола та побудувати коло. а) з центром у точці O і радіусом б) з центром у точці (-2;5) і радіусом 3; в) знайдіть координати точок перетину кола х г) складіть рівняння кола, що проходить через (2;8), (4;-6), (-12;-6).
Завдання 2. Складіть канонічне рівняння еліпса та побудуйте його : а) якщо дві його вершини знаходяться в точках А1(-6,0), А2(6,0), а фокуси F1(-4,0), F2(4,0); б) з фокусами на осі Ох, якщо його велика вісь 10, ексцентриситет ε =0,6; в) якщо відомо, що відстань між фокусами дорівнює 8, а мала вісь 2b = 6; г) якщо відстань між фокусами дорівнює 6(фокуси лежать на осі Ох) і велика вісь дорівнює 10.
Завдання 3. Скласти канонічне рівняння гіперболи та здійснити побудову. а) з фокусами на осі Ох, якщо її дійсна вісь 16, а уявна 8; б) якщо координати її вершин А в) відстань між фокусами 2с=10, а між вершинами 2а=8; г) вісь в=4, а відстань між фокусами 2с=10.
Завдання 4. Скласти канонічне рівняння параболи та здійснити побудову: а) парабола розташована у правій півплощині симетричне відносно осі Ох і її параметр р = 3; б) з вершиною в початку координат, якщо її фокус лежить в точці: 1) F в) з вершиною в початку координат, якщо її директрисою є пряма: 1) х =-2; 2) х = 3; 3) у = -4; г) з віссю симетрії паралельною осі Ох, якщо6 1) парабола проходить через точку М(1;3) і має вершину А(-4;-2); 2) парабола проходить через початок координат і має вершину А(-2;-4).
Завдання 5. а) знайдіть довжину відрізка прямої х+4у-28=0, що лежить всередині еліпса х2/400 + у2/25 = 1; б)знайдіть вершини, фокуси. асимптоти, ексцентриситет гіперболи в)знайдіть точки перетину параболи у 2х-у+2=0; г) складіть рівняння спільної хорди двох кіл, які перетинаються х2 + у2 – 6у = 0, х2 + у2 – 12х = 0.
|
|
 .
.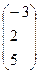 , В= (4 -4 -1).
, В= (4 -4 -1). в) А=
в) А=  , В=
, В=  .
. , В=
, В=  .
. , В=
, В=  .
. ; В=
; В=  ; С=
; С=  . D=
. D=  ; P=
; P= 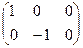
 ;В=
;В=  ; С=
; С=  ; Д=
; Д=  .
. ; В=
; В=  ; С=
; С=  ; Д=
; Д=  Е=
Е=  F=
F=  .
. 2)
2)  3)
3) 
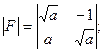 5)
5)  6)
6)  .
. 2)
2)  3)
3)  4)
4) 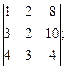 5)
5)  ; 6)
; 6) 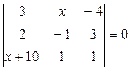
 2)
2)  3)
3) 
 5)
5)  ;6)
;6)  .
. 2)
2) 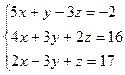 3)
3)  4)
4)  5)
5)  6)
6) 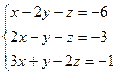
 8)
8) 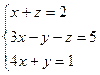
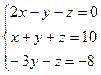
 2)
2)  3)
3)  4)
4)  5)
5)  6)
6) 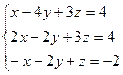
 8)
8)  9)
9) 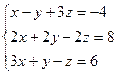
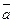 = (2,3),
= (2,3),  =(-1,2),
=(-1,2), 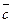 =(3,1). Знайти координати векторів:
=(3,1). Знайти координати векторів:  ,
,  ; 2)
; 2) 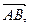 де А ( 1, 3) , В( -2, 0);
де А ( 1, 3) , В( -2, 0); 4)
4)  де М( -1,5,2), N( 2,5,-2)
де М( -1,5,2), N( 2,5,-2) і
і  ;
;  і
і  ,якщо А(3;1), В(7;4), С(3;2), Д(6;6).
,якщо А(3;1), В(7;4), С(3;2), Д(6;6). :
:  =1:7.
=1:7. : 1)Мо(-2;-3),
: 1)Мо(-2;-3), 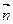 =(4;-5); 2) Мо(1;-1),
=(4;-5); 2) Мо(1;-1),  х+1 4) х-2у-4=0 та 2х-4у+3=0
х+1 4) х-2у-4=0 та 2х-4у+3=0 =(5;2;-3) і
=(5;2;-3) і  =(1;4;-2).
=(1;4;-2). ;
;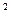 +у
+у  (-3;0), А
(-3;0), А  (3;0) та координати фокусів F
(3;0) та координати фокусів F  (-5;0), F
(-5;0), F  (0;2);
(0;2); ;
;