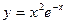|
|
Тема3. Вступ до математичного аналізу.Практичне заняття 3.1. Тема: Функціональна залежність. Основні елементарні функції. Властивість функцій.
Мета:З’ясувати поняття функціональної залежності між величинами; дослідити властивості основних елементарних функцій; навчитись знаходити область визначення функцій, досліджувати їх на парність та непарність, періодичність. Завдання1.Знайти значення функції в даних точках: а) F(xy) = x б) f(х) = 2cos4x + в) f(х) = ln
Завдання 2.Знайти область визначення функції, задана формулами. а) y= в) y=log д) y=arcsin(x+3); е) y=arcos(x+2); є) y=ln(-x)+
Завдання 3. Дослідити функцію на парність та знайти період. 1) y= 2x-x
Практичне заняття 3.2.1 Тема: Знаходження границь послідовності. Мета:Засвоїти поняття: числова послідовність, обмежені та необмежені послідовності, нескінченно малі та нескінченно великі величини, збіжні послідовності; навчитися знаходити границі збіжних послідовностей. Завдання 1. Знайти границі. 1) 7)lim (1+
Практичне заняття 3.2.2 Тема:Знаходження границь функції . Дослідження функції на безперервність.
Мета: Закріпити поняття: границя функції,нескінченно малі та нескінченно великі величини, неперервність функції в точці; пояснити важливість знаходження границь функцій для дослідження їх на неперервність; навчитися знаходити границі, застосовуючи основні теореми про границі, розкриваючи невизначеності типу 0/0, ∞/∞ та використовуючи чудові границі.
Заняття 1. Знайти границі функції. 1) 4) 7) 10) 13)
Завдання 2.Знайти границі функції. 1) 7) 10) Завдання 3.Знайти границі функції. 1) 4) 7) 10) Тема4. Диференціальне числення функції однієї змінної. Практичне заняття 4.1 Тема.Знаходження похідних функції. Мета:Закріпити поняття похідної функції та її геометричного, механічного та економічного змісту. Добитися вміння автоматичного знаходження похідних основних елементарних функцій; відпрацювати навики знаходження похідних, застосовуючи основні правила диференціювання. Навчитися знаходити похідні складних функцій та функцій, заданих неявно і параметрично.
Завдання 1.Знайти похідні першого порядку. 1) у=2х 3) у=4х 7) y=arcsinx+4 9) y=
Завдання 2.Знайти похідні складних функцій: 1) y=cos 3) y=cosx+lnx 4) y=lnsinx 5) y=e 7) y= 2 9) y=arcsin
Завдання 3.Знайти похідні другого порядку таких функцій: 1) y=e 3) y=cos 5) y= x*e
Завдання 4.Знайти похідні функцій, заданих параметрично: 1) Завдання 5.Знайти похідні функцій, заданих неявно:
1) x siny-y cosx=0 2) e 3)
Практичне заняття 4.2. Тема: Диференціал функції. Застосування диференціала до наближених обчислень. Мета:Пояснити поняття диференціала функції. З’ясувати різницю між диференціалом та приростом функції в даній точці. Відпрацювати диференціали до наближених обчислень.
Завдання1. Знайти диференціали першого порядку функції. 1) 3) y=ln(sinx) 4) y= 5) y= 7) 9)
Завдання 2. Обчислити наближене значення функції у вказаних точках: 1)f(x)= 2)f(x)= 3)f(x)= 4)f(x)=x*ln(x-2) в точці х=3,012 5)f(x)=e
Завдання 3.Обчислити наближено: 1) 10 4) ln 7) (1.03)
Практичне заняття 4.3 Тема: Основні теореми диференціального числення. Правило Лопіталя. Мета:Вивчити основні теореми диференціального числення з метою подальшого їх застосування для дослідження функцій та побудови їх графіків. Навчитись розкривати невизначеності типу 0/0, ∞/∞, 0∙∞, ∞ - ∞, ∞0 , 00, застосовуючи правило Лопіталя.
Завдання 1. Використовуючи правило Лопіталя, знайти границі:
1) 3) 5) 7) 9) Завдання 2. Використовуючи правило Лопіталя, розкрийте невизначеності: 1) 3) 5)
Практичне заняття 4.4. Тема: Дослідження функцій та побудова їх графіків.
Мета: Дати практику дослідження функції та побудови їх графіків. Систематизувати знання з теми «Диференціальне числення функцій однієї змінної». Навчитись застосовувати навички знаходження границь функцій, похідні функції, розкриття невизначеностей за правилом Лопіталя до дослідження функцій та побудови їх графіків. Завдання 1. Знайти інтервали зростання, спадання та екстремуми функції: 1) y= 3) y= x∙lnx 4)y= 5) y=15-x
Завдання 2. Знайти інтервали опуклості функції та точки перетину функції: 1) y= 3) y= 5) y=
Завдання 3. Знайти найбільше і найменше значення функції на вказаному відрізку. 1)y= 3)y=sinx+2x, [П;-П] 4)y= 5)y=
Завдання 4. Дослідити функції та побудувати їх графіки. 1) y=x 3) y= 5) y= 7) y= 9)
|
|
 -3ху-у
-3ху-у 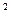 при х = 4, у = 3;
при х = 4, у = 3; при х=0;
при х=0; при х=1; г) f(х) =
при х=1; г) f(х) =  при х=1.
при х=1. б) y= 3cos2x +
б) y= 3cos2x +  ;
; ;
;  г) y=
г) y=  ;
;  ; ж) y= 3
; ж) y= 3  -
-  ;
; sinx. 3) y= x - 2
sinx. 3) y= x - 2  . 4) y=
. 4) y=  . 5) y=
. 5) y=  . 6) y= sinx – cosx.
. 6) y= sinx – cosx. . 2)
. 2)  3)
3)  . 4)
. 4)  . 5)
. 5) 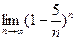 . 6)
. 6)  .
. . 8)
. 8)  . 9)
. 9)  .
. , 2)
, 2)  , 3)
, 3)  .
. 5)
5)  , 6)
, 6)  .
. . 8)
. 8)  9)
9) 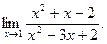
 . 11)
. 11) 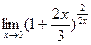 . 12)
. 12) 
 . 14)
. 14)  , 15)
, 15)  ,
, 2)
2)  , 3)
, 3) 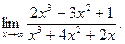 4)
4)  , 5)
, 5)  , 6)
, 6) 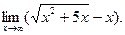
 , 8)
, 8)  , 9)
, 9)  .
. , 11)
, 11) 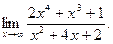 12)
12)  .
.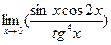 , 2)
, 2)  , 3)
, 3)  .
. 5)
5)  , 6)
, 6)  .
. 8)
8)  9)
9) 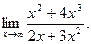
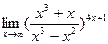 . 11)
. 11)  . 12)
. 12) 
 2) у=
2) у= 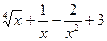
 4) y=
4) y=  5) y=log
5) y=log  6) y=2
6) y=2 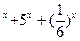
 8) y=
8) y= 
 10) y=
10) y= 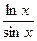
 2) y=
2) y= 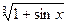
 6) y =
6) y = 
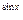 8) y=arcos(1-2x)
8) y=arcos(1-2x) 10) y=(tgx)
10) y=(tgx)  2) y=
2) y= 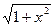
 4) y=
4) y= 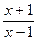
 2)
2)  3)
3)  4)
4) 
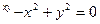
 4)
4) 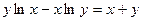
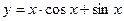 2)
2) 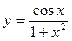
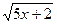
 6)
6) 
 8)
8) 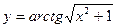
 10)
10) 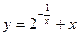
 в точці х=1,003
в точці х=1,003 в точці х=1,01
в точці х=1,01 в точці х=3,032
в точці х=3,032 в точці х=3,97.
в точці х=3,97. 2) 1,025
2) 1,025 
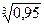
 5) e
5) e  6) 10
6) 10 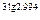
 8)
8)  9)
9) 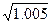

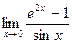
 4)
4) 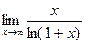
 6)
6) 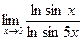
 8)
8) 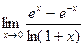
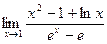 10)
10) 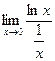
 2)
2) 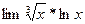
 4)
4) 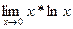
 6)
6) 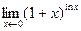
 2)y=x
2)y=x 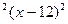
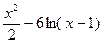
 6)y=e
6)y=e 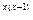
 2)y=
2)y= 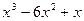
 4)y=
4)y= 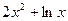
 6)
6) 
 2)y=
2)y=  [-3;7]
[-3;7] . [0;1]
. [0;1] .[-5;5] 6)y=x
.[-5;5] 6)y=x  . [-1;4]
. [-1;4] 2) y=
2) y= 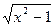
 4) y=
4) y= 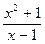
 6) y=x*lnx
6) y=x*lnx 8) y=
8) y= 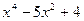
 10)
10)