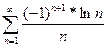|
|
Тема 5. Диференціальне числення функції багатьох змінних.Практичне заняття 5.1.1 Тема: Функції багатьох змінних. Границя функції багатьох змінних. Мета:Засвоїти поняття функції багатьох змінних. Навчитися знаходити області визначення функції багатьох змінних, області неперервності, точки розриву. Дти практику обчислення границь функцій багатьох змінних.
Завдання1. Знайти значення функції у вказаних точках: 1) f(x.y.z)=x 2) f(x.y.z)= 3) f(x.y)=
Завдання 2. Знайти область визначення функції, заданих рівняннями: 1) z = 3) z = 5) z = 7) z = ln(4x 9) z =
Завдання 3. Обчислити границі функції багатьох змінних: 1) 3) 5) 7) 9)
Практичне заняття 5.1.2. Тема: Частинні похідні функції багатьох змінних. Похідні вищих порядків. Повний диференціал. Мета: Дати практику знаходження частинних похідних першого порядку та вищих порядків функції багатьох змінних, повного диференціалу. Засвоїти поняття градієнта функції багатьох змінних та його механічного змісту. Навчитися обчислювати наближено значення функції в точці, замінюючи її повний приріст повним диференціалом. Дати навички обчислення похідних складних функцій. Завдання1.Знайти частинні похідні першого порядку функцій двох змінних: 1) z=x 3) z=x 5) z= 7) z= 9) z=
Завдання 2.Знайти повні диференціали функцій двох змінних: 1) z=xy 3) z= 5) z= 7) z=y 9) z=
Завдання 3.Знайти градієнт grad Z та [grad Z] функції двох змінних в даній точці: 1) z=x 3) z=
Завдання 4. Обчислити наближено значення: 1)(1,08) 3)sin 1.59 * tg 3.09 4) 2.68
Практичне заняття 5.2 Тема: Екстремуми функцій двох змінних. Знаходження умовного екстремуму функції двох змінних методом Лагранжа. Мета: Засвоїти поняття екстремуму функцій багатьох змінних на прикладах функцій двох змінних. Закріпити навички знаходження частинних похідних першого та другого порядків функцій двох змінних та навчитися застосовувати їх до знаходження екстремумів функцій двох змінних, використовуючи необхідні умови існування екстремуму функцій багатьох змінних та достатні умови існування екстремуму функцій двох змінних. Засвоїти поняття умовного екстремуму функцій багатьох змінних. Навчитись знаходити умовний екстремум функцій двох змінних методом Лагранжа. Закріпити навички знаходження частинних похідних першого порядку та обчислення визначників третього порядку Завдання 1.Знайти екстремуми функції двох змінних: 1) z = x 3) z = 5) z = 2x 7) z = x 9) z = y
Завдання 2.Знайти екстремум функції Z=(x.y). за умови 1) z = xy за умови x 2) z = x 3) z = x 4) z = xy 5) z = x 6) z = xy за умови х+у=10 7) z = xy 8) z = 10x+y за умови 9) z = x 10) z = x
Практичне заняття 5.3 Тема:Визначення параметрів функціональної залежності методам найменших квадратів Мета: Навчатись визначати вид функціональної залежності змінних величин х та у в процесі, що досліджується. Дати практику застосування методу найменших квадратів для оцінки невідомих параметрів лінійної та параболічної функціональних залежностей. Література: Завдання 1. Величина товарообміну Х(тис.грн) та витрати обігу У(грн.) задані таблицею
Знайти аналітичну залежність між величинами Х та У.
Завдання 2.Величина товарообміну Х(ти. Грн.) та витрати обігу У(грн.) задані таблицею
Знайти аналітичну залежність між величинами Х та У.
Завдання 3.В таблиці вказано кількість внесених добрив на 1 га(Х) та врожай пшениці (У) у центнерах.
Обрати вигляд аналітичної залежності між величинами Х та У і визначити її параметри.
Завдання 4.Методом найменших квадратів визначити параметри лінійної функціональної залежності між величинами Х та У:
Тема 6. Інтегральне числення та диференціальні рівняння. Практичне заняття 6.1. Тема:Невизначений інтеграл. Метод безпосереднього інтегрування, метод інтегрування заміною змінних. Мета: Засвоїти поняття первісної функції, невизначеного інтегралу, основні правила інтегрування, дати практику знаходження невизначеного інтегралу за допомогою таблиці основних інтегралів, методом безпосереднього інтегрування та методом заміни змінної. Література: Завдання 1.Знайти невизначений інтеграл, використовуючи правила та таблицю основних інтегралів: 1) 3) 5) 7) 9)
Завдання 2.Знайти невизначений інтеграл, використовуючи метод заміни змінної. 1) 3) 5) 7) 9)
Практичне заняття 6.2. Тема:Невизначений інтеграл. Метод Інтегрування частинами, інтегрування дробово-раціональних функцій. Мета: Дати практику знаходження невизначеного інтеграла методом інтегрування частинами, інтегрування дробово-раціональних функцій методом невизначених коефіцієнтів. Закріпити вміння знаходити інтеграл методом заміни змінної та за допомогою таблиці основних інтегралів. Повторити поняття первісної функції, невизначеного інтеграла, основні правила інтегрування функцій.
Завдання 1.Знайти невизначений інтеграл, використовуючи формулу інтегрування частинами. 1) 3) 5) 7) 9)
Завдання 2.Знайти невизначений інтеграл від дробово-раціональних функцій, застосовуючи метод невизначених коефіцієнтів: 1) 3) 5) 7) 9)
Практичне заняття 6.3.1 Тема: Визначений інтеграл. Формула Ньютона-Лейбніца. Методи обчислення визначених інтегралів: заміна змінних та формула інтегрування частинами. Мета: Дати практику обчислення визначених інтегралів заміною змінних та за формулою інтегрування частинами. Засвоїти основні властивості визначених інтегралів, умову інтегрованості функції на відрізку. Показати зв’язок між визначеним та невизначеним інтегралами. Повторити основні методи інтегрування функцій, зокрема інтегрування дробово-раціональних, трибометричних та ірраціональних функцій. Завдання 1.Обчислити визначений інтеграл. 1) 3) 5) 7) 9) 11) 13) 15) 17) 19)
Практичне заняття 6.3.2 Тема: Геометричне застосування визначеного інтеграла : обчислення площі плоскої фігури, довжини дуги плоскої кривої, об’єму та площі поверхні тіла обертання.
Мета:Навчитись застосовувати на практиці вміння знаходити визначений інтеграл до обчислення площі плоскої фігури, довжини дуги плоскої кривої, об’єму та площі поверхні тіла обертання. Закріпити навички дослідження функцій та побудова їх графіків.
Завдання 1. Обчислити площу фігури, обмеженої кривою y=f(x), віссю Ох та прямими х=а, х=b: 1)y=-x 3)y=1-x
Завдання 2. Обчислити площу фігури, обмеженої лініями: 1) y = x 3) y = x 5) y = sin2x. y=1. x=
Завдання 3.Обчислити довжину дуги плоскої кривої: 1) напівкубічної параболи у=х 2) кривої у=х 3) кривої у=х
Завдання 4. Обчислити об’єм: 1)тіла, утвореного обертанням еліпса 2)тіла, утвореного обертанням фігури, обмеженої лініями у=х 3)у=е
Завдання 5. Знайти площу поверхні, утвореної обертанням навколо осі Ох: 1) півкола у= 2) дуги синусоїди y=sin x від х=0 до х=П. 3) дуги кривої у Практичне заняття 6.4. Тема: Диференціальні рівняння. Загальний розв’язок. Задача Коші. Диференціальні рівняння з відокремленими змінними.
Мета: Дати практику розв’язку диференціальних рівнянь першого порядку: рівнянь з відокремленими змінними та автономних рівнянь. Закріпити поняття: загальний розв’язок диференціального рівняння та розв’язок задачі Коші, інтеграл рівняння, інтегральна крива, порядок диференціального рівняння.
Завдання 1.Перевірити , чи є вказані функції розв’язками диференціальних рівнянь: 1)у=Сх., у’x-y=0; 2) у=х 3) у=е 5) Завдання 2.Розв’язати автономні диференціальні рівняння: 1) 3) y’= 5)
Завдання 3.Знайти загальний розв’язок або загальний інтеграл диференціальних рівнянь з відокремленими змінними: 1)y’=2x*(y-1) 3) xydx+(x+1) dy=0 4) 5) (x+1)dy-(y-2)dx=0 6)
Завдання 4. Розв’язати задачу Коші: 1) xdy=ydx y(2)=6 2) 3) y’ 4) 5) 6)
Практичне заняття 6.5 Тема: Лінійні та однорідні диференціальні рівняння Мета: Дати практику розв’язку лінійних та однорідних диференціальних рівнянь першого порядку. Повторити поняття: загальний розв’язок диференціального рівняння та розв’язок задачі Коші, інтеграл рівняння, інтегральна крива. Закріпити навички знаходження невизначених інтегралів.
Завдання 1.Знайти загальні розв’язки лінійних диференціальних рівнянь:
1) y’ + y = 2 2) xy’ -3y = x4 3) x’ – 3x = e-t
4) y’ + 2y = 4x 5) y’ – y = ex 6) xy’ – y = x
7) y’ + x2y = x2 8) y’ + y = cosx 9) xy’ + 2y = x2
Завдання 2.Знайти загальні розв’язки однорідних диференціальних рівнянь:
1) (x+y)dy + xdy = 0 2) (x+y)dy + (y-x)dy = 0
3) ( x-y)dx + xdy = 0 4) ( 2
5) xy2dy=(x3 + y3)dx; y=3 при х = 1 6) ( x2+y2)dx = xydy; y=0 при x=1
7) (x-y)dy = y dy; y = 1 при x=0 8) xcos(y/x)dy – y cos(y/x)dx+xdx=0; y=0 при x=1.
Завдання 3.Знайти загальні розв’язки однорідних диференціальних рівнянь другого порядку з сталими коефіцієнтами:
1) y’’ + y’ – 6y = 0 2) y’’ – 8y + 15y = 0 3) y’’ + 5y + 6 = 0
4) y’’ – 9 y’ = 0 5) y’’ + 3y = 0 6) y’’ – y = 0
7) y’’ + 9y = 0 8) y’’ -2y + 5y = 0 9) y’’ + 4y + 7y = 0
10) y’’ + 3y’ + 4y = 3sin5x 11) y’’ – 4y = x2 + 3
12) y’’ – 4y + 3y = 5ex
Тема 7. Числові ряди Практичне заняття 7.1 Тема:Числові ряди. Ознаки збіжності рядів Мета: Засвоїти поняття: знакосталі та знакозмінні ряди, абсолютна та умовна збіжність рядів. Дати практику дослідження рядів з додатними членами на збіжність за ознаками порівняння, Даламбера, Коші, інтегральною ознакою Коші. Навчитись досліджувати абсолютну та умовну збіжність знакопочергових рядів за ознакою Лейбніца. Завдання 1. Перевірити, чи виконується необхідна умова збіжності рядів: 1) 3) 5)
Завдання 2. Використовуючи ознаку порівняння, дослідити збіжність рядів 1) 3) 5)
Завдання 3.За допомогою ознаки Даламбера дослідити ряди на збіжність: 1) 3) 5)
Завдання 4. За допомогою ознаки Коші дослідити ряди на збіжність: 1) 3) Завдання 5. Дослідити на абсолютну та умовну збіжність рядів: 1) 3) 5) ЕКЗАМЕНАЦІЙНІ ПИТАННЯ З ВИЩОЇ МАТЕМАТИКИ ВСТУП. 1. Предмет математики. Зв¢язок математики з економікою. 2. Економіко-математичне моделювання. Задача планування виробництва. ТЕМА 1: ЛІНІЙНА АЛГЕБРА. 3. Поняття матриці. Задачі, які приводять до поняття матриці. Застосування матриць в економічних розрахунках. 4. Різновиди матриць. Дії над матрицями: додавання та множення, множення на число. Елементарні перетворення. Знаходження рангу матриць. 5. Визначники другого та третього порядків. Обчислення визначників n-го порядку. Властивості визначників. Розклад визначників за елементами рядків та стовпців. 6. Обернені матриці. Способи обчислення обернених матриць. 7. Системи лінійних алгебраїчних рівнянь: основні означення та поняття. Матричний запис. Застосування систем лінійних рівнянь у лінійному моделюванні. Теорема Кронекера-Капеллі сумісності та визначеності систем. 8. Методи обчислення визначників. Теорема Крамера. Розв¢язування систем рівнянь за формулами Крамера. 9. Матричний метод розв¢язування систем лінійних рівнянь. 10. Розв¢язування систем лінійних рівнянь методом Гаусса, Гаусса-Жордана. |
|
 в точках Мо(1,2,3), М(-2,1,-4)
в точках Мо(1,2,3), М(-2,1,-4)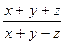 . (x.y.z)=(
. (x.y.z)=( 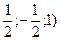
 , Мо(1,-2), М(3,-2), М2(2,-2).
, Мо(1,-2), М(3,-2), М2(2,-2). 2) z =
2) z = 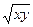
 4) z =
4) z = 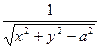
 6) z = ln(x+y)
6) z = ln(x+y)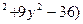 8) z =
8) z = 
 10) z =
10) z = 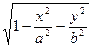
 2)
2) 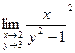

 4)
4) 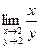
 6)
6) 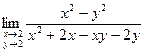
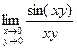 8)
8) 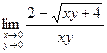
 10) lim
10) lim  .
. x
x 
 4) z=
4) z= 
 6) z=
6) z= 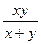
 8) z=ln(
8) z=ln( 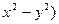
 10) z=
10) z= 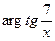
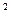 2) z=xy
2) z=xy 4) z=sinxy
4) z=sinxy  6) z=xy*cosxy
6) z=xy*cosxy 8) z=tg
8) z=tg 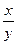
 10) z=ln(4-x
10) z=ln(4-x 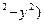
 , Мо(2,-1). 2) z=4-x
, Мо(2,-1). 2) z=4-x  , Мо(1,2)
, Мо(1,2) , Мо(0,3) 4) z=(x-y)
, Мо(0,3) 4) z=(x-y)  2)1,94
2)1,94 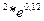
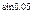 .
. 2) z = xy(1-x-y)
2) z = xy(1-x-y) 4) z = e
4) z = e 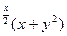
 6) z = 3
6) z = 3 
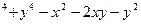 8) z = x
8) z = x 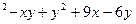
 10) z = y
10) z = y 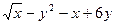
 (x.y)=0:
(x.y)=0: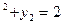
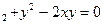
 за умови x+y=2, x
за умови x+y=2, x 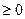 .y=
.y= 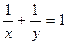
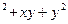 за умови x
за умови x 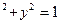
 за умови х+у=2, х
за умови х+у=2, х 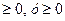
 2)
2) 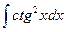
 4)
4) 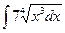
 6)
6) 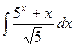
 8)
8) 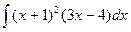
 10)
10) 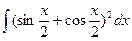
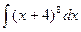 2)
2) 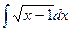
 4)
4) 
 6)
6) 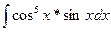
 8)
8) 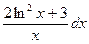
 10)
10) 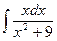
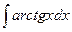 2)
2) 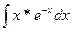
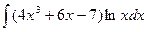 4)
4) 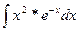
 6)
6) 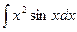
 8)
8) 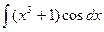
 10)
10)  .
. 2)
2) 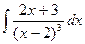
 4)
4) 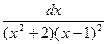
 6)
6) 
 8)
8) 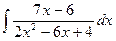
 10)
10) 
 2)
2) 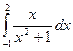
 4)
4) 
 6)
6) 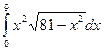
 8)
8) 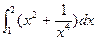
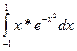 10)
10) 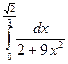
 12)
12) 
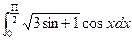 14)
14) 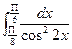
 16)
16) 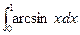
 18)
18) 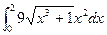
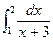 20)
20) 
 . x=ln2. x=ln5
. x=ln2. x=ln5 .
. . y=0. x=-2. x=1.
. y=0. x=-2. x=1.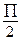 . –П/4
. –П/4  П/2, 6) xy=4. x=4. y=4. x=0. y=0.
П/2, 6) xy=4. x=4. y=4. x=0. y=0. від х=0 до х=4,
від х=0 до х=4, ;
; навколо осі Ох.
навколо осі Ох. ,
, від х=0 до х=3.
від х=0 до х=3. , у’=3x
, у’=3x  , у’=2y; 4) у=е
, у’=2y; 4) у=е  , у’=-y+1;
, у’=-y+1; . y’-ycosx=
. y’-ycosx=  .
. 2)
2) 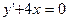
 4)
4) 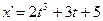
 6)y’=x+sinx.
6)y’=x+sinx.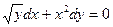
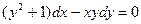
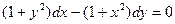
 y(3)=1
y(3)=1 y(1)=5
y(1)=5 y(4)=1
y(4)=1 y(0)=1
y(0)=1 y(-1)=1
y(-1)=1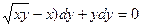
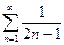 , 2)
, 2) 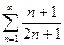

 4)
4) 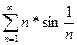
 6)
6) 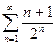 .
.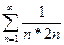
 4)
4) 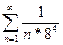
 6)
6) 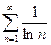
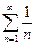 2)
2) 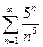
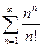
 6)
6) 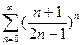 2)
2) 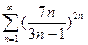
 4)
4) 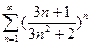
 2)
2) 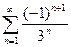
 4)
4) 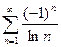
 6)
6)