|
|
Метод еталонів, що дробляться
Цей метод спрямований на усунення модельності метода еталонів шляхом наближення до практичних задач, для яких є характерним перетин класів. На рисунку 2.2.1. зображено класи, які перетинаються. Тут
Рисунок 2.2.1
Якщо гіперсфери перетинаються і в області перетину знаходяться реалізації більше ніж одного класу, то для них будуються контейнери другого рівня, потім третього, і т. д. До тих пір, поки контейнери не будуть перетинатися або в області перетину залишаться реалізації одного класу. Переваги : - метод враховує реальні апріорні розбиття класів розпізнавання, тобто що вони перетинаються; - метод є відносно простий. Недоліки : - контейнери різних рівнів не є оптимальними в інформаційному розумінні; - оскільки реалізації на практиці є випадковими, то фактична достовірність розпізнавання на екзамені може суттєво відрізнятися від асимптотичної достовірності, одержаної на етапі навчання, тобто цей метод не характеризується високою достовірністю розпізнавання. Лінійні вирішальні правила
За цим методом роздільна гіперповерхня задається у вигляді лінійної функції
де Лінійні вирішальні правила застосовуються у випадку лінійно поділених векторів реалізацій образу. Нехай, для випадку двох класів (
Рисунок 2.3.1.
У цьому випадку, алгоритм розпізнавання буде дуже простим:
IF
Якщо Одним із прикладів реалізації лінійних вирішальних правил є перцептрон Розенблата (рис.2.3.2). Тут
Рисунок 2.3.2
Задача навчання штучної нейромережі зводиться до цілеспрямованого підбору вагових коефіцієнтів з тим, щоб на виході перцептрона отримати мінімальну помилку
де Сигнал
Рисунок 2.3.3
Лінійні вирішальні правила можуть застосовуватися для нормальних образів, тобто для класів розпізнавання, що не перетинаються. Якщо класи перетинаються, для них навчальна вибірка не є нормально розподіленою, а вектори- реалізації образів не є лінійно поділеними.
Метод найближчих сусідів За методом найближчих сусідів на етапі навчання побудова роздільних гіперповерхонь в просторі ознак розпізнавання здійснюється шляхом запам’ятовування всіх реалізацій образів і віднесення невідомої реалізації до того класу, “представник” якого знаходиться найближче до цієї реалізації. Відносно методу інформаційно-екстремальної інтелектуальної технології (ІЕІТ) [], де цей принцип використовується на етапі навчання, таким представником виступає ядро класу розпізнавання, тобто для контейнерів класів розпізнавання, які побудовані в реальному базисі бінарного простору ознак, це є вершини відповідних двійкових еталонних векторів-реадізацій. Основний недолік методу найближчих сусідів – метод не працює у загальному випадку, коли класи перетинаються.
2.5. Метод
За цим методом будується гіперсфера обсяг При цьому основна проблема полягає у побудові гіперсфери Цей основний недолік відсутній в методах ІЕІТ, оскільки вона дозволяє в процесі навчанння побудувати оптимальні, в інформаційному розумінні, контейнери класів розпізнавання. Безпосередньо, принцип К найближчих сусідів в ІЕІТ реалізується на етапі екзамену. Метод потенційних функцій
Нехай
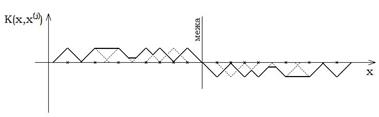
де За визначенням потенційна функція є спадковою по мірі збільшення відстані поточної координати Вибір потенційної функції не є простою задачею, яку доводиться розв’язувати розробнику інформаційного забезпечення систем розпізнавання. Від вибору потенційної функції залежить як збіжність алгоритму, так і його точність. На рис. 2.6.1 наведено приклад побудови вирішального правила за методом потенційних функцій.
Рисунок 2.6.1
Таким чином, процес навчання за методом потенційних функцій полягає в побудові вирішального правила (2.6.1.). Тоді процес розпізнівання за цим методом може здійснюватись за таким алгоритмом: якщо в точці
IF
Зауваження: при великих обсягах навчальної вибірки доцільно обчислювати не вирішальне правило (2.6.1.), а оцінювати розподільну межу для класів розпізнавання (рис. 2.6.1.). У цьому випадку для підвищення оперативності розпізнавання достатньо лише визначити де знаходиться реалізація – справа чи зліва від межі. Подальше узагальнення метода потенційних функцій полягає в його рандомізації шляхом побудови роздільної межі за навчальною вибіркою з використанням процедур стохастичної апроксимації . Переваги: - простота реалізації, яка грунтується на фізичних законах електростатики (чим далі від заряду, тим менше його вплив). Недоліки: - необхідність обгрунтування вибору потенційної функції, яка впливає безпосередньо на збіжність алгоритму навчання та на достовірність розпізнавання в режимі екзамену. - vетод носить модельний характер, оскільки орієнтований на класи що не перетинаються у просторі ознак розпізнавання. |
|
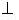 ,
,  – графічне зображення реалізацій класів
– графічне зображення реалізацій класів 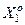 і
і  відповідно.
відповідно.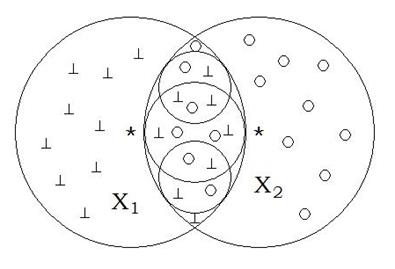
 ,
,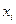 –
– 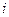 -та ознака розпізнавання.
-та ознака розпізнавання.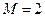 ) розподіл їх векторів-реалізацій показано на рис. 2.3.1.
) розподіл їх векторів-реалізацій показано на рис. 2.3.1.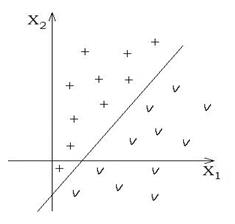
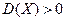 THEN
THEN 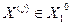 ELSE
ELSE 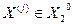
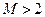 , то функція роздільної гіперповерхні буде у вигляді не однієї лінійної функції, а у вигляді кусочно-лінійної функції.
, то функція роздільної гіперповерхні буде у вигляді не однієї лінійної функції, а у вигляді кусочно-лінійної функції. – блоки множення, ПЕ – пороговий елемент.
– блоки множення, ПЕ – пороговий елемент.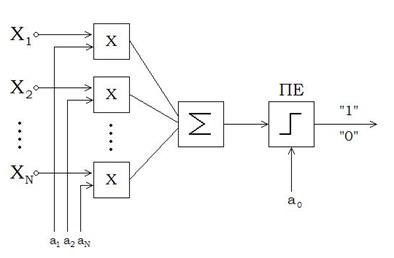
 ,
,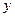 – вихід штучної нейромережі;
– вихід штучної нейромережі;  – директивний сигнал (вказівка “учителя”).
– директивний сигнал (вказівка “учителя”).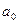 безпосередньо впливає на поріг спрацьовування порогового елементу (рис.2.3.3).
безпосередньо впливає на поріг спрацьовування порогового елементу (рис.2.3.3).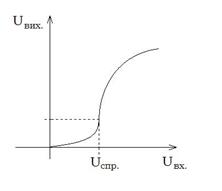
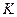 найближчих сусідів
найближчих сусідів , з центром у вершині вектора-реалізації
, з центром у вершині вектора-реалізації 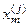 . На екзамені розпізнавання хдійснюється за більшістю представників деякого класу, які знаходяться в середині гіперсфери.
. На екзамені розпізнавання хдійснюється за більшістю представників деякого класу, які знаходяться в середині гіперсфери. . Відома координата вершини вектора-реалізації
. Відома координата вершини вектора-реалізації 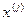 в просторі ознак. Надамо точці, що знаходиться в цій координаті потенціал
в просторі ознак. Надамо точці, що знаходиться в цій координаті потенціал  , якщо
, якщо 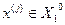 , і потенціал
, і потенціал 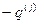 , якщо
, якщо 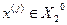 . Тоді може мати місце таке вирішальне правило, що створюється
. Тоді може мати місце таке вирішальне правило, що створюється  потенціалами:
потенціалами: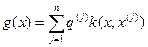 , (2.6.1.)
, (2.6.1.)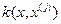 – потенційна функція.
– потенційна функція.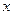 від вершини
від вершини 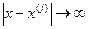 .
.
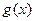 і отримуємо правило
і отримуємо правило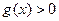 THEN
THEN