|
|
Структурні (лінгвістичні методи)
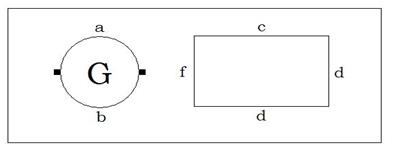
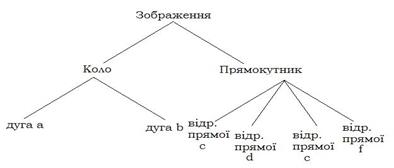
При структурних методах, реалізації образу характеризують не множиною їх значень (наприклад, навчальна матриця типу об’єкт-властивість) або їх відношень (наприклад, навчальна матриця типу відношень-схожості), а їх структурою. Наприклад, на рис. 2.7.1. наведено зображення, яке можна описати його ієрархічною структурою (рис.2.7.2):
Рисунок 2.7.1.
Рисунок –2.7.2
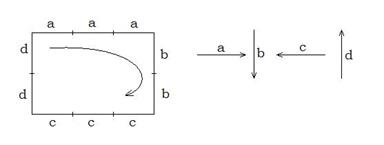
Структурний підхід грунтується на аналогії між структурою реалізації образу та синтаксисом мов, тому він часто називається лінгвістичним. Етап розпізнавання за структурними методами полягає в розпізнаванні не похідних елементів реалізацій образу і синтаксичному аналізі (граматичний розбір) “речення”, що описує образ. Приклад формування “речення”показано на рис. 2.7.3.
Рисунок 2.7.3
Структурні методи знайшли широке використання при сегментації (при визначенні меж) різних текстур [], при усномовному розпізнаванні за послідовністю фонем [ ] та інше. Основна перевага – це можливість подати велику кількість реалізацій у вигляді малопотужної множини непохідних елементів і граматичних правил. Недоліки: - відсутність прямих вирішальних правил. - обмеженість використання через те, що аналізується не весь образ, а тільки його фрагмент, що ускладнює процес прийняття рішень. Методи кластер-аналізу
Кластер-аналіз (класифікаційний аналіз, навчання без учителя, таксономія, самонавчання) розв’язує такі основні задачі: - факторний кластер-аналіз, що полягає у визначенні нового класу для відкритого алфавіту класів розпізнавання - тдиційний кластер-аналіз, який полягає в побудові розбиття простору ознак за апріорною не класифікованою навчальною вибіркою, за умови незмінної потужності словника ознак - самонавчання, яке розв’язує задачу традиційного кластер-аналізу за умови зміни потужності відкритого словника До теперішнього часу проблема кластер-аналізу (тобто розбиття простору ознак розпізнавання за апріорною навчальною вибіркою) залишається не вирішеною. В основі кластер-аналізу лежить гіпотеза компактності (чіткої або не чіткої ). Тобто навчальна вибірка у просторі ознак складається із множини згущень реалізацій образів, які мають відповідні центри їх розсіювання. Реалізації, що відносяться до одного згущення, яке будемо називати таксоном, є найближчими до еталонного вектора- реалізації, який визначає центр розсіювання реалізації і є найближчими відносно векторів інших таксонів. При цьому поняття “близькість” розглядається у загальному випадку як міра різноманітності реалізації образів, яка є функціоналом як від дистанційних критеріїв, так і критеріїв зв’язності між реалізаціями. Розглянемо метод кластер-аналізу в геометричній інтерпритації. Класичним представником таких методів є метод FOREL. Ідея цього методу полягає в побудові в просторі ознак гіперсфери радіуса За множиною точок вершин реалізацій, що належать гіперсфері, визначається середнє значення координат і внього пересувається центр гіперсфери. Оскільки в поточну гіперсферу попали додатково інші точки, то процедура їх усереднення повторюється і відповідно центр гіперсфери не пересувається в нову усереднену координату і т.д. поки не зупиниться. Тоді всі точки, що належать цій гіперсфері виключаються із розгляду і процес повторюється до тих пір, поки не будуть використані всі точки. Таким чином, результатом таксономії є множина гіперсфер (формальних елементів) радіуса Таким чином, метод FOREL не дозволяє побудувати чітке розбиття еквівалентності класів розпізнавання. Основний недолік алгоритма FOREL полягає в тому, що результати таксономії залежать від початкового вибору центру гіперсфери радіуса Методом кластер-аналізу, який базується на критеріях зв’язності є критерій KRAB. В основу метода покладено обчислення інтегрованого критерію якості таксономії:
де
Тут
де
Параметри
де
Якщо довжина
де І нарешті, параметр
тобто це усереднена по всім таксонам міра близькості точок, де
– усереднена міра близькості в середині Таким чином, стверджується, що чим більше функціонал
Розділ 3.Статистичні методи ТРО
Статистичні методи розпізнавання поділяють на параметричні методи, для яких відомі закони розподілу імовірностей (має функцію щільності), та непараметричні методи, для яких відсутня інформація про закон розподілу ймовірностей (випадкові величини).
3.1. Байесівський класифікатор
Параметричні методи реалізуються на базі байєсівського класифікатора (вирішальних правил) за відповідними статистичними критеріями теорії прийняття рішень [3]. Класифікатор називається байєсівським тому, що теоретичною основою його створення є класична формула Байєса, яка дозволяє обчислити апостеріорну умовну імовірність через апріорні умовні імовірності, наприклад, для двохальтернативних рішень за формолою :
де Розглянемо основні статистичні критерії. Критерій максимальної апостеріорної умовної імовірності. За цим критерієм, якщо відомо, наприклад, відношення апостеріорних умовних імовірностей
то приймається рішення, що Якщо виконується принцип Бернуллі-Лапласа (
За допомогою відношення правдоподібності (3.1.2) в статистичній теорії прийняття рішень реалізується критерій максимуму правдоподібності[3], який дозволяє мінімізувати повну ймовірність помилкового рішення:
.
При цьому алгоритм розпізнавання такий: якщо
то Вимоги практичного застосування байєсівських класифікаторів сприяли розвитку непараметричного підходу в ТРО, у рамках якого, наприклад, запропоновано функцію умовного середнього ризику:
де Для мінімізації умовного середнього ризику функція штрафів повинна мати по діагоналі нулі, а всі інші елементи не повинні дорівнювати нулю. На практиці широке застосування знайшов статистичний критерій Неймана-Пірсона, який дозволяє мінімізувати вираз (3.1.3) при заданих обмеженнях на одну із помилок. Звичайно приймається
3.2. Визначення мінімального обсягу репрезентативної навчальної вибірки
З метою усуненя основного недоліку відомих непараметричних методів, який пов’язаний з необхідністю наявності великого обсягу навчальної вибірки, актуальною є задача визначення мінімального обсягу репрезентативної навчальної вибірки. Оскільки вибірки випадкових величин є скінченними, то це обумовлює наявність статистичної похибки, яка є основним критерієм репрезентативності навчальної вибірки:
де При цьому За теоремою Муавра-Лапласа встановлено, що має місце співвідношення
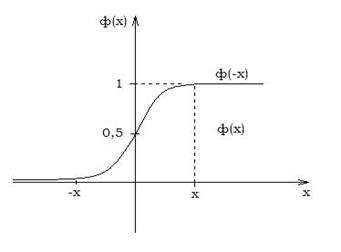
де Оскільки графік функції Лапласа має вигляд, показаний на рис. 2.9.1, то можна прийняти, що
Рисунок 3.2.1
Тоді
На рис 3.2.2 наведено графічний приклад визначення мінімального обсягу репрезентативної навчальної вибірки
Рисунок 3.2.2
За рис. 3.2.2 як Таким чином, при Основною заслугою статистичного підходу до розпізнавання образів є започаткування розвитку теорії машинного навчання, основи якої закладено у працях [8,10,14]. При цьому модельність статистичних методів автоматичної класифікації так само становить певну методологічну цінність, оскільки дозволяє дослідити механізм прийняття рішень.
|
|
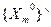 , де
, де 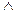 - символ відкритості множини, елементи якої не є скінченними.
- символ відкритості множини, елементи якої не є скінченними. , де
, де 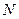 - кількість ознак розпізнавання.
- кількість ознак розпізнавання.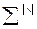 , тобто самонавчання передбачає розв’язання таких задач як оцінка інформативності ОР та оптимізація словника ознак.
, тобто самонавчання передбачає розв’язання таких задач як оцінка інформативності ОР та оптимізація словника ознак.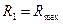 .
.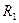 з центрами визначеними за вище наведеним алгоритмом. Такий процес називається циклом з формальним елементом радіуса
з центрами визначеними за вище наведеним алгоритмом. Такий процес називається циклом з формальним елементом радіуса 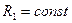 ). У наступному циклі аналогічно будуються гіперсфери радіуса
). У наступному циклі аналогічно будуються гіперсфери радіуса 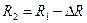 , де
, де 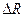 - параметр функціонування системи розпізнавання, який впливає як на оперативність алгоритму, так і на точність розбиття простору ознак на таксони.
- параметр функціонування системи розпізнавання, який впливає як на оперативність алгоритму, так і на точність розбиття простору ознак на таксони.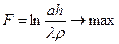 , (2.8.1)
, (2.8.1)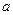 - середня довжина ребер, що з’єднують таксони:
- середня довжина ребер, що з’єднують таксони: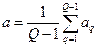 ,
,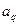 - довжина ребер одного таксона:
- довжина ребер одного таксона: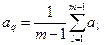 ,
,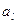 – довжина
– довжина 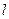 -го ребра
-го ребра  -го таксона;
-го таксона; – кількість точок в таксоні.
– кількість точок в таксоні.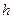 і
і 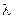 у виразі (2.8.1) визначаються відповідно за формулами
у виразі (2.8.1) визначаються відповідно за формулами ,
,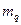 - кількість точок
- кількість точок 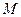 - загальна кількість усіх точок;
- загальна кількість усіх точок;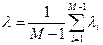 .
.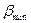 , то чим менше буде
, то чим менше буде  , тим більше є причин вважати що саме по ребру здовжиною
, тим більше є причин вважати що саме по ребру здовжиною  ,
,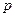 визначається за формулою
визначається за формулою ,
,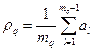
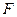 , тим його якість буде вища. Отже процес таксономії є найбільш ефективним. Тобто вони дозволяють побудувати апріорне нечітке розбиття простору ознак на класи. Тобто цей підхід може бути використаний на підготовчому етапі для застосування ІЕІТ.
, тим його якість буде вища. Отже процес таксономії є найбільш ефективним. Тобто вони дозволяють побудувати апріорне нечітке розбиття простору ознак на класи. Тобто цей підхід може бути використаний на підготовчому етапі для застосування ІЕІТ. , (3.1.1)
, (3.1.1)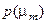 – безумовна ймовірність належності
– безумовна ймовірність належності 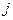 -ої реалізації
-ої реалізації  класу
класу  ;
;  – апріорна умовна ймовірність прийняття гіпотези
– апріорна умовна ймовірність прийняття гіпотези 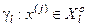 за умови, що мала місце апріорна гіпотеза
за умови, що мала місце апріорна гіпотеза  .
. ,
,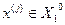 .
.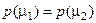 ), то можна використовувати відношення правдоподібності
), то можна використовувати відношення правдоподібності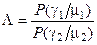 , (3.1.2)
, (3.1.2)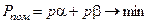 . (3.1.3)
. (3.1.3)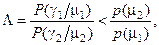
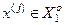 , інакше
, інакше 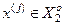 .
.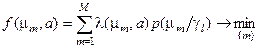 , (3.1.4)
, (3.1.4)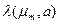 - функція штрафів (втрат) при прийнятті гіпотези
- функція штрафів (втрат) при прийнятті гіпотези 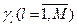 .
.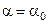 . Тоді за поріг класифікації приймається величина
. Тоді за поріг класифікації приймається величина 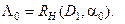
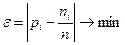 ,
,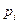 – імовірність знаходження
– імовірність знаходження 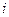 - ої ознаки розпізнавання в своєму контрольному полі допусків
- ої ознаки розпізнавання в своєму контрольному полі допусків 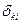 ;
; 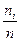 – емпірична частота.
– емпірична частота.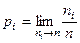 –граничне значення емпіричної частоти.
–граничне значення емпіричної частоти.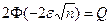 ),
), – функція Лапласа;
– функція Лапласа;  – рівень значущості, який дорівнює будь-якому малому додатньому числу, але рекомендується вибирати із такого ряду чисол: Q=00,5; 0,01; 0,001;
– рівень значущості, який дорівнює будь-якому малому додатньому числу, але рекомендується вибирати із такого ряду чисол: Q=00,5; 0,01; 0,001;  – обсяг навчальної вибірки.
– обсяг навчальної вибірки.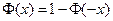 .
.

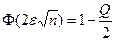 , звідки
, звідки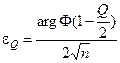 . (3.2.1)
. (3.2.1)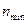 . При цьому графік залежності статистичної похибки
. При цьому графік залежності статистичної похибки  від обсягу вибірки
від обсягу вибірки 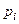 побудовано за формулою
побудовано за формулою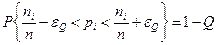 . (3.2.3)
. (3.2.3)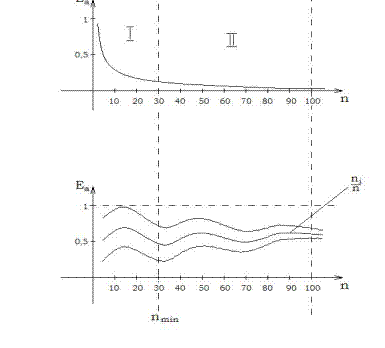
 , де
, де  , повністю покриває довірчий інтервал (2.9.3).
, повністю покриває довірчий інтервал (2.9.3).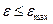 і далі буде мати місце статистична стійкість. Застосування навчальних вибірок обсягу
і далі буде мати місце статистична стійкість. Застосування навчальних вибірок обсягу