|
|
Побудова часткової моделі нечіткого МГУА (НМГУА)Для побудови часткової моделі НМГУА використовувалася лінійна інтервальна регресійна модель, що задається таким чином:
де
Виходячи з цього,
Відношення вкладеності двох інтервалів У нашому випадку зміні
Розглянемо метод оцінювання лінійної інтервальної регресійної моделі. Нехай є
Побудова робиться з урахуванням наступних вимог: 1.Задані значення 2.Ширина оціночного інтервалу повинна бути мінімальною. Ці вимоги можна звести до задачі лінійного програмування в наступному вигляді (для
Виходячи з цього, при відомих значення перемінних
при обмеженнях
де Завдання полягає у тому, щоб мінімізувати область зміни вихідних значень Вирішивши двоїсту задачу симплекс-методом і одержавши оптимальні значення двоїстих змінних, ми зможемо знайти й оптимальні значення шуканих змінних Опис ряду селекції Щоб одержати моделі другого ряду необхідно задати опорну функцію, аргументами якої є функції-моделі, отримані у попередньому ряді. У нашому випадку опорна функція задавалася також поліномом другого ( У кожному ряді після генерації всіх можливих моделей за комплексним критерієм у площині критеріїв відбиралися
При генерації моделей може виникнути явище индуцита, що зв’язане з тим, що після ряду ітерацій Приклад отриманих результатів виконаних експериментів для заданої задачі про макроекономічні показники. Результати структурної ідентифікації на вікні прогнозування розміром у 15 точок, з яких 10 було виділено на навчальну й 5 – на перевірочну вибірку. При ідентифікації на наступний етап синтезу передавалося 10 кращих моделей поточного етапу. Використовуваний частковий опис:
Величина СКП: 0,7119462.
Загальний опис алгоритму
2.Вибір зовнішніх критеріїв оптимальності і свободи вибору. 3.Вибір загального виду опорної функції (для багаторядних алгоритмів МГУА). 4.Покласти нульові значення лічильнику числа моделей 5.генеруємо нову часткову модель. Визначаємо значення основних критеріїв на ній. Присвоїти 6.Якщо 7.Якщо 8.З Переваги нечіткого МГУА - відсутня проблема поганої обумовленості матриць, оскільки нема необхідності застосовувати МНК, а задача лінійного програмування завжди має розв’язок; - отримуємо інтервальну, а не точкову оцінку прогнозованої величини, що дозволяє оцінити точність одержуваних прогнозів; - застосування нечіткого МГУА в задачах прогнозування економічних процесів зі складною динамікою та невідомим функціональним взаємозв’язком між процесами є цілком аргументованим і дозволяє отримати відносно високу точність пронозу; - використання адаптації коефіцієнтів знайденої нечіткої моделі за поточними даними дозволяє підвищити точність прогнозування на 15-20%; результати прогнозування за НМГУА практично мало залежать від типу функції належності. 1. Васильев В. И. Распознающие системы. Справочник. 2-е изд., перераб. и доп.- Киев: Наукова думка, 1983.- 422 с. 2. Краснопоясовський А.С. Інформаційний синтез інтелектуальних систем керування: Підхід, що ґрунтується на методі функціонально-статистичних випробувань.- Суми: Видавництво СумДУ, 2004. - 261 c. 3. Краснопоясовський А.С. Класифікаційний аналіз даних: Навчальний посібник.- Суми: Видавництво СумДУ, 2002.- 159 с. 4. Турбович И. Т., Гитис В. Г., Маслов В. К. Опознание образов. Детерминир.-статист. подход.-М.: Наука, 1971.- 246 с. 5. Анисимов Б. В., Курганов В. Д., Злобин В. К. Распознавание и цифровая обработка изображений.- М.: Высшая школа, 1983.–256 с. 6. Методы анализа данных: Подход, основанный на методе динамических сгущений: Пер. с фр. / Кол. авт. под рук. Э. Дидэ / Под ред. и с предисл. С. А. Айвазяна и В. М. Бухштабера.- М.: Финансы и статистика, 1985.-375 с. 7. Загоруйко Н. Г., Елкина В. Н., Лбов Г. С. Алгоритмы обнаружения эмпирических закономерностей. - Новосибирск: Наука. -1985. - 110 с. 8. Прикладная статистика: Классификация и снижение размерности. Справ. изд./ С.А. Айвазян, В.М. Бухштабер, И.С. Енюков, Л.Д. Мешалкин / Под ред. С.А. Айвазяна.- М.: Финансы и статистика, 1989- 607 с. 9. Shalkoff R.J. Digital image processing and computer vision. – New York-Chichester-Brisbane-Toronto-Singapore: John Wiley & Sons, Inc., 1989. – 489 p. 10. Duda R. O., Hart P. E., Stork D. G. Pattern Classification, second ed. John Wiley & Sons, New York, 2001.- 738 p. 11. Путятин Е.П., Аверин С.И. Обработка изображений в робототехнике. М: Машиностроение, 1990.– 320 с. 12. Костюк В.И., Гаврик А.П., Ямпольский Л.С., Карлов А.Г. Промышленные роботы: Конструирование, управление, эксплуатация. – К.: Вища шк. Головное изд-во, 1985.– 359 с. 13. Зайченко Ю.П. Основи проектування інтелектуальних систем: Навчальний посібник.– К.: Видавничий Дім «Слово», 2004.– 352 с. 14. Вапник В. Н., Червоненкис А. Я. Теория распознавания образов: (статистические проблемы обучения).- М.: Наука, 1974.- 416 с. 15. Осовский С. Нейронные сети для обработки информации: Пер. с польського И.Д. Рудинского.– М.: Финансы и статистика, 2004.– 344 с. 16. Беллман Р., Заде Л. Принятие решений в расплывчатых условиях. В кн.: Вопросы анализа и процедуры принятия решений.- М.: Мир, 1976.- С. 172 - 216. 17. Кузьмин И. В., Кедрус В. А. Основы теории информации и кодирования. Учебное пособие. - К.: Вища школа, 1977.-415 с. 18. Цымбал B. П. Основы теории информации и кодирования.- Киев: Ви ща школа, 1977. - 288 с. 19. Горелик А. П., Скрыпкин В. А. Методы распознавания.- М.: Высшая школа, 1984.- 207 с. 20. Курейчик В.М. Генетические алгоритмы. – Таганрог: ТРТУ, 1998.– 242 с. 21. Гаскаров Д. В., Голинкевич Т.А., Мозгалевский A.В. Прогнозирование технического состояния и надёжности радиоэлектронной аппаратуры. - М.: Сов. радио, 1974. - 223 с. 22. Бобровников Г. Н., Клебанов А. И. Прогнозирование в управлении техническим уровнем и качеством продукции: Учебное пособие.- М.: Изд-во стандартов, 1984. - 232 с. |
|
 ,
, ‑ деякі відомі перемінні,
‑ деякі відомі перемінні,  ‑ інтервали, які можна задати трикутними нечіткими числами і записати таким чином у вигляді центра
‑ інтервали, які можна задати трикутними нечіткими числами і записати таким чином у вигляді центра  і ширини
і ширини  :
: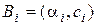 .
. можна розрахувати так:
можна розрахувати так: .
.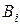 і
і  (
( 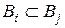 ) можна задати наступними нерівностями:
) можна задати наступними нерівностями:  .
.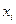 і
і  дл відповідної часткової моделі НМГУА так:
дл відповідної часткової моделі НМГУА так: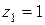 ,
,  ,
,  ,
,  , …,
, …,  ,
,  .
.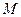 спостережень
спостережень 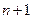 перемінної, причому
перемінної, причому  з них – незалежні величини, (
з них – незалежні величини, (  ми намагаємося визначити. При цьому
ми намагаємося визначити. При цьому  і
і  ‑ вхідні і вихідні вектори точок спостереження. Тоді оціночна лінійна інтервальна модель для часткової моделі НМГУА має вигляд:
‑ вхідні і вихідні вектори точок спостереження. Тоді оціночна лінійна інтервальна модель для часткової моделі НМГУА має вигляд: .
.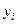 , що спостерігаються, включаються в оціночний інтервал
, що спостерігаються, включаються в оціночний інтервал  .
. -тої точки спостереження):
-тої точки спостереження): ; (4.1)
; (4.1) ; (4.2)
; (4.2) ; (4.3)
; (4.3) .
.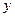 , отриманих у результаті
, отриманих у результаті 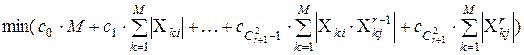 ; (4.4)
; (4.4) ,
, , які забезпечували б мінімальне розсіювання величини
, які забезпечували б мінімальне розсіювання величини  і
і  , а разом з цим і визначити шукану модель математичної залежності.
, а разом з цим і визначити шукану модель математичної залежності. -того) ступеня від двох змінних, тобто
-того) ступеня від двох змінних, тобто 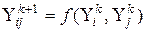 , де
, де 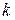 ‑ номер ряду.
‑ номер ряду. кращих моделей, що беруть участь у подальшій генерації. Критерієм зупинки процесу генерації є близькість середнього критерію моделей на двох сусідніх рядах роботи методу, тобто:
кращих моделей, що беруть участь у подальшій генерації. Критерієм зупинки процесу генерації є близькість середнього критерію моделей на двох сусідніх рядах роботи методу, тобто: .
. .
.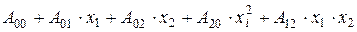 .
. .
. , то
, то  . Складаємо середній критерій моделей ряду
. Складаємо середній критерій моделей ряду  . Якщо
. Якщо  , то переходимо на крок 5, інакше – на крок 7.
, то переходимо на крок 5, інакше – на крок 7. , то йдемо на крок 8, інакше вибираємо
, то йдемо на крок 8, інакше вибираємо