Проблемы и их решение: Экономико-математическая модель

Для организации важен как механизм управления процессом решения проблем, так и исполнительный механизм реализации решений.

С точки зрения эффективной адаптации организации к реальным условиям функционирования исключительно важная роль принадлежит механизму управления процессом решения проблем и, следовательно, процессом принятия решений.

К функциям управления процессом решения проблем организации относятся прежде всего:

Предвидение проблем,

Выявлением проблем,

Диагностика,

Систематизация и классификация проблем,

Выработка альтернативных вариантов решений,

Выбор наиболее предпочтительного альтернативного варианта решения (собственно принятие решения),

Реализация принятых решений,

Контроль за реализацией решений.

Проблемы, возникновение которых ожидается, целесообразно проранжировать по важности, обращая внимание в первую очередь на наиболее важные из них, которые могут оказать существенное влияние на функционирование организации.

Выявление проблем предполагает тщательный анализ текущей деятельности организации. Этот анализ может проводиться как пассивными, так и активными методами.

К числу пассивных могут быть отнесены методы, связанные с анализом поступающей в организацию информации или информации, непосредственно относящейся к области функционирования и полученной из внешних источников, в частности из специальных аналитических обзоров прессы, банков данных и т.д.

К числу активных методов выявление проблем относятся прежде всего методы, связанные с использованием опыта и знаний экспертов, специально собранной информации, целенаправленно проведенного исследования.

Выявленные проблемы, так же как и на этапе прогнозирования, должны быть проранжированны по важности. Из них должны быть отобраны те, которые представляют наибольшую опасность либо открывают принципиально новые возможности для развития организации.

После того как проблема выявлена, она должна быть диагностирована с целью определения ее характера и специфики.

Приведем экономико-математическую модель выбора первоочередных (приоритетных проблем), стоящих перед организацией, для их первоочередного решения, построенную с использованием методов смешанного (линейного и целочисленного программирования.

Поскольку один из основных аспектов управления организацией – распределение ресурсов, а определение первоочередности проблем решения проблем. Стоящих пред организацией, и есть, по сути, задача рационального распределения ресурсов, то модель целесообразно рассматривать как модель оптимального распределения ресурсов, исходя из сравнительной экономической эффективности заказов и проблем, соответственно выполняемых или решаемых организаций.

Пусть имеется перечень из n (i = 1, …, n) заказов, которые организация может выполнить в рассматриваемый промежуток времени, и m (j = 1, …, m) проблем, которые возникают в тот период и требуют своего решения.

Ожидаемая прибыль при выполнении i-го заказа равна C_r. При решении j-ой проблемы может быть получена дополнительная прибыль D_j (если дополнительной прибыли при решении этой проблемы нет, то D_j =0). Если же эта проблема не решена, то организация понесет потери – Z_j.

Обозначим через X_i переменную соответствующую заказу с номером i и принимающую значения от X_i min до X_i max – от минимально возможного уровня обеспечения i-го заказа ресурсом до максимально возможного.

Суммарный ресурс k-го вида обозначим через R_k; через R_ik – количество ресурса k-го вида, необходимое для выполнения i-го заказа, а через R_jk – количество ресурса k-го вида, необходимое для решения j-ой проблемы.

Тогда задача оптимального распределения ресурсов для организации формулируется следующим образом:

,

при ограничениях

,

.

Y_j = 1, если j-ая проблема решена организацией, 0-в противном случае.

Можно непосредственно убедиться в том, что сформулированная выше экономико-математическая модель содержит задачу определения как первоочередных заказов для выполнения, стоящих перед организацией в связи с их решением.

Чтобы получить первую из упомянутых задач, достаточно положить значения переменных Y_j = 0, j = 1, …, m. А чтобы получить вторую задачу – достаточно положить значения переменных X_i = 0, i = 1, …, n.

Решение первой из задач позволит нам определить первоочередные проблемы, которые целесообразно выполнить организации, если предполагается, что решение возникающих проблем не решается за счет этих же ресурсов.

Решение второй задачи позволит определить первоочередные проблемы, которые надо решить организации, если эти же ресурсы не могут потребоваться для выполнения заказов.

Решение же полной задачи, сформулированной выше, позволит определить заказы, которые необходимо выполнять в первую очередь при наличии стоящих перед организацией проблем, и проблемы, которые необходимо выполнять в первую очередь при наличии у организации потока заказов.

Таким образом, только полная задача, соответствующая сформулированной выше экономико-математической модели, позволит дать ответ на вопрос, какие заказы и какие проблемы необходимо решать в первую очередь при имеющихся в распоряжении руководителя организации ресурсах.

Лекция № 2
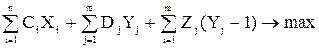