Гармонічні коливання і їх характеристики С. Г. Авдєєв, Т. І. Бабюк
Лекції з фізики
(коливання і хвилі, оптика)
Міністерство освіти і науки України
Вінницький національний технічний університет
С. Г. Авдєєв, Т. І. Бабюк
Лекції з фізики
(коливання і хвилі, оптика)
Затверджено Вченою радою Вінницького національного технічного університету як курс лекцій для студентів електротехнічних спеціальностей. Протокол № 7 від 27 грудня 2007 р.
Вінниця ВНТУ 2008
УДК 53 (075)
А 75
Рецензенти:
П. М. Зузяк, доктор фізико-математичних наук, професор
І. О. Сівак, доктор технічних наук, професор
В. Г. Дзісь,кандидат технічних наук, доцент
Рекомендовано до видання Вченою радою Вінницького національного технічного університету Міністерства освіти і науки України.
Авдєєв С. Г., Бабюк Т. І.
А 75 Лекції з фізики, (коливання і хвилі, оптика). Курс лекцій, – Вінниця: ВНТУ, 2008. – 138с.
Посібник складено у відповідності з планом кафедри та програмою дисципліни курсу фізики для технічних вузів і пропонується студентам всіх форм навчання.
УДК 53 (075)
© С. Г. Авдєєв, Т. І. Бабюк, 2008
| З М І С Т
Тема 1. Механічні й електромагнітні коливання.....................................5
1 Гармонічні коливання і їх характеристики............................................ 5
2 Механічні гармонічні коливання............................................................... 8
3 Гармонічний осцилятор. Пружинний, фізичний і математичний
маятники...................................................................................................... 10
4 Вільні гармонічні коливання в коливальному контурі...................... 14
Тема 2. Додавання гармонічних коливань..............................................17
1 Додавання гармонічних коливань однакового напрямку і однакових частот. Биття................................................................................................17
2 Додавання взаємно перпендикулярних коливань. Фігури Ліссажу...... 22
3 Диференціальне рівняння вільних згасаючих коливань і його
розв’язування............................................................................................ 27
Тема 3. Вимушені механічні й електромагнітні коливання....................31
1 Диференціальне рівняння вимушених коливань і його розв’язування..31
2 Амплітуда і фаза вимушених коливань (механічних і
електромагнітних). Резонанс. Резонансні криві. Параметричний
резонанс.................................................................................................. 35
3 Змінний струм.........................................................................................38
4 Резонанс напруг.....................................................................................44
Тема 4. Пружні хвилі...................................................................................45
1 Хвильові процеси. Поздовжні і поперечні хвилі................................ 45
2 Рівняння біжучої хвилі. Фазова швидкість. Сферична хвиля............ 47
3 Одновимірне хвильове рівняння. Швидкість поширення хвиль......... 50
4 Енергія пружних хвиль. Потік і густина потоку енергії хвиль............54
Тема 5. Суперпозиція хвиль......................................................................57
1 Принцип суперпозиції хвиль. Групова швидкість................................. 57
2 Інтерференція хвиль.................................................................................. 58
3 Стоячі хвилі................................................................................................. 61
Тема 6. Електромагнітні хвилі..................................................................64
1 Природа електромагнітних хвиль............................................................. 64
2 Хвильові рівняння електромагнітних хвиль............................................ 67
3 Енергія електромагнітних хвиль. Вектор Пойнтінга.............................. 71
Тема 7. Інтерференція світла.....................................................................74
1 Принцип накладання двох хвиль. Інтенсивність. Поняття когерент-
ності хвиль.................................................................................................. 74
2 Інтерференція світла від двох когерентних джерел. Дослід Юнга...... 78
3 Інтерференція в тонких плівках. Кільця Ньютона................................. 81
4 Інтерференція багатьох хвиль................................................................... 86
Тема 8. Дифракція світла............................................................................89
1 Метод зон Френеля. Дифракція Фраунгофера на круглому отворі....... 89
2 Дифракція Фраунгофера на щілині........................................................... 94
3 Дифракційна решітка. Кутова дисперсія і роздільна здатність
дифракційної решітки................................................................................ 98
4 Дифракція рентгенівських променів на просторовій решітці. Формула Вульфа-Брегга...........................................................................................102
Тема 9. Поляризація світла....................................................................103
1 Природне і поляризоване світло...............................................................103
2 Поляризація світла при відбиванні. Закони Брюстера й Малюса....... 107
3 Подвійне променезаломлення. Звичайний і незвичайний промені.
Призма Ніколя.......................................................................................... 109
4 Штучна оптична анізотропія. Обертання площини поляризації……..114
Тема 10. Квантова природа випромінювання
1 Теплове випромінювання і його характеристики.......................................... 120
2 Закон Кірхгофа.................................................................................................... 122
3 Закони Стефана – Больцмана і Віна................................................................ 124
4 Формула Планка. Виведення законів Стефана-Больцмана і Віна........ 125
5 Зовнішній фотоефект. Ефект Комптона......................................................... 128
|
|
Використана література ...........................................................................137
Тема 1. Механічні й електромагнітні коливання
Гармонічні коливання і їх характеристики.
Механічні гармонічні коливання.
Гармонічний осцилятор. Пружинний, фізичний і математичний маятники.
Вільні гармонічні коливання в коливальному контурі.
Гармонічні коливання і їх характеристики
Коливаннями називаються рухи або процеси, які характеризуються певною повторюваністю в часі. Коливальні процеси широко поширені в природі й техніці, наприклад, коливання маятника годинника, змінний електричний струм і т. д. При коливальному русі маятника змінюється координата його центра мас, а у випадку змінного струму – коливаються напруга й струм у колі. Фізична природа коливань може бути різною, тому розрізняють коливання механічні, електромагнітні й ін. Однак різні коливальні процеси описуються однаковими характеристиками й однаковими рівняннями. Звідси випливає доцільність єдиного підходу довивчення коливань різної фізичної природи.
Коливання будуть вільними (або власними), якщо вони відбуваються за рахунок деякої енергії, переданої коливальній системі в початковий момент часу, при відсутності в наступні моменти часу будь-яких зовнішніх впливів на цю систему. Найпростішими коливаннями є гармонічні коливання, при яких коливна величина змінюється з часом за законом косинуса або синуса. Вивчення гармонічних коливань важливе з двох причин:
1) коливання, які зустрічаються у природі й техніці, при певних наближеннях є гармонічними;
2) різні періодичні процеси (процеси, які повторюються через рівні проміжки часу), можна подавати як суперпозицію гармонічних коливань.
Гармонічні коливання деякої фізичної величини х описуються таким рівнянням
 (1) (1)
де А – максимальне значення коливної величини x, яке називається амплітудою коливань;
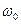 – колова, або циклічна частота; – колова, або циклічна частота;
φ – початкова фаза коливань для моменту часу t = 0;
 – фаза коливань для довільного моменту часу t. – фаза коливань для довільного моменту часу t.
Оскільки косинус змінюється в межах від +1 до -1, то х може набувати значень від +А до -А.
Певні стани системи в процесі гармонічних коливань повторюються
через однаковий проміжок часу Т, якийназивається періодом коливань. За цей час фаза коливання зростає на 2π, тобто
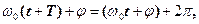
звідки
 (2) (2)
Величина, обернена до періоду коливань
 (3) (3)
виконана коливною системою за одиницю часу, називається частотою коливань. Прирівнюючи (2) і (3), одержимо
ω0 = 2  . .
Одиницею частоти є герц (Гц), це частота такого періодичного процесу, при якому за 1 с відбувається одне повне коливання.
Запишемо першу й другу похідні фізичної величини х гармонічного коливання, тобто визначимо швидкість і прискорення коливання:
 (4) (4)
 (5) (5)
тобто маємо гармонічні коливання тієї ж циклічної частоти. Амплітуди величин (4) і (5) відповідно дорівнюють  і і  . Фаза швидкості (4) відрізняється від фази фізичної величини (1) на π/2, а фаза прискорення (5) відрізняється від фази фізичної величини (1) на π. . Фаза швидкості (4) відрізняється від фази фізичної величини (1) на π/2, а фаза прискорення (5) відрізняється від фази фізичної величини (1) на π.
Отже, у моменти часу, коли х = 0,  має найбільші значення; коли ж x досягає максимальних від’ємних значень то в ці моменти часу має найбільші значення; коли ж x досягає максимальних від’ємних значень то в ці моменти часу  будуть мати найбільші додатні значення (рис. 1). будуть мати найбільші додатні значення (рис. 1).
З рівняння (5) одержуємо диференціальне рівняння гармонічних коливань (де враховано, що х = Acos (ωοt + φ)),
 . (6) . (6)

Рис. 1
Таким чином, розв’язком диференціального рівняння (6) є вираз (1).
Гармонічні коливання можна зобразити графічно за допомогою методу обертання вектора амплітуди або методу векторних діаграм.Для цього з довільної точки О, взятої на осі х, під кутом φ, який дорівнює початковій фазі коливання, відкладається вектор  , модуль якого дорівнює амплітуді А гармонічного коливання (рис. 2). , модуль якого дорівнює амплітуді А гармонічного коливання (рис. 2).
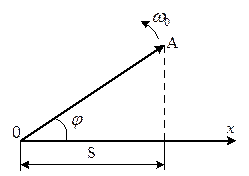
Рис. 2
Якщо цей вектор привести до обертання з кутовою швидкістю 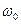 то проекція кінця вектора буде переміщуватися по осі x і набувати значень від -А до + А, а коливна величина буде змінюватися з часом за законом х = Acos(ωοt + φ). У фізиці часто застосовується інший метод, який відрізняється від методу обертання вектора амплітуди лише за формою. У цьому методі коливну величину подають комплексним числом відповідно до формули Ейлера для комплексних чисел то проекція кінця вектора буде переміщуватися по осі x і набувати значень від -А до + А, а коливна величина буде змінюватися з часом за законом х = Acos(ωοt + φ). У фізиці часто застосовується інший метод, який відрізняється від методу обертання вектора амплітуди лише за формою. У цьому методі коливну величину подають комплексним числом відповідно до формули Ейлера для комплексних чисел
 (7) (7)
де  – уявна одиниця. Тому рівняння гармонічного коливання (1) можна записати також в експонентній формі так: – уявна одиниця. Тому рівняння гармонічного коливання (1) можна записати також в експонентній формі так:
 (8) (8)
Права частина рівняння (8) є рівнянням гармонічних коливань.
|

 (1)
(1)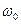 – колова, або циклічна частота;
– колова, або циклічна частота; – фаза коливань для довільного моменту часу t.
– фаза коливань для довільного моменту часу t.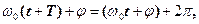
 (2)
(2) (3)
(3) .
. (4)
(4) (5)
(5) і
і  . Фаза швидкості (4) відрізняється від фази фізичної величини (1) на π/2, а фаза прискорення (5) відрізняється від фази фізичної величини (1) на π.
. Фаза швидкості (4) відрізняється від фази фізичної величини (1) на π/2, а фаза прискорення (5) відрізняється від фази фізичної величини (1) на π. має найбільші значення; коли ж x досягає максимальних від’ємних значень то в ці моменти часу
має найбільші значення; коли ж x досягає максимальних від’ємних значень то в ці моменти часу  будуть мати найбільші додатні значення (рис. 1).
будуть мати найбільші додатні значення (рис. 1). . (6)
. (6)
 , модуль якого дорівнює амплітуді А гармонічного коливання (рис. 2).
, модуль якого дорівнює амплітуді А гармонічного коливання (рис. 2).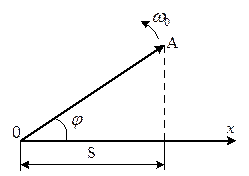
 (7)
(7) – уявна одиниця. Тому рівняння гармонічного коливання (1) можна записати також в експонентній формі так:
– уявна одиниця. Тому рівняння гармонічного коливання (1) можна записати також в експонентній формі так: (8)
(8)