|
|
Случайная погрешность и количество измерениий.Для уменьшения случайной погрешности есть два пути: повышение точности измерений (уменьшение σх) и увеличение числа измерений n с целью использования соотношения (14). Считая, что все возможности совершенствования техники измерений использованы, рассмотрим второй путь. При этом отметим, что уменьшать случайную составляющую погрешности целесообразно лишь до тех пор, пока общая погрешность измерений не будет полностью определяться систематической составляющей Δс. Если систематическая погрешность определяется классом точности СИ Δси (или γси), то необходимо, чтобы доверительный интервал Обычно принимают от Для сравнения случайных погрешностей с различными законами распределения использование показателей, сводящих плотность распределения к одному или нескольким числам, обязательно. В качестве таких чисел и выступают СКО, доверительный интервал и доверительная вероятность.
Надежность самого СКО характеризуется величиной
Принято, что если σσ≤0,25σ, то оценка точности надежна. Это условие выполняется уже при n=8. Наиболее вероятная погрешность Δв отдельного измерения определяется по формуле
Анализ этой формулы показывает, что с увеличением n величина Δв быстро уменьшается лишь до n=5 ... 10. Следовательно, увеличение числа измерений на одном режиме свыше 5... 10 нецелесообразно, что совпадает с условием получения надежных значений σσ. Число измерений можно выбрать по одной из формул:
где nот — число отбрасываемых экспериментальных результатов. С учетом коэффициентов Стьюдента можно оценить относительную погрешность отдельного измерения как Определение систематических погрешностей. Как правило, считают, что систематические погрешности могут быть обнаружены и исключены. Однако в реальных условиях полностью исключить систематическую составляющую погрешности невозможно. Всегда остаются какие-то не исключенные остатки, которые и нужно учитывать, чтобы оценить их границы. Это и будет систематическая погрешность измерения. То есть в принципе систематическая погрешность тоже случайна, и указание деление обусловлено лишь установившимися традициями обработки и представления результатов измерения. Оставшаяся необнаруженной систематическая составляющая опаснее случайной: если случайная составляющая вызывает вариацию (разброс) результатов, то систематическая — устойчиво их искажает (смещает). В любом случае отсутствие или незначительность (с целью пренебрежения) систематической погрешности нужно доказать. Действительно, если взять два ряда измерений одной и той же величины, то средние результаты этих рядов, как правило, будут различны. Это расхождение может быть определено случайной или систематической составляющей. Методика выявления характера погрешности заключается в следующем: 1. Из двух рядов n1 и n2 независимых измерений находят средние арифметические х1, и х2. 2. Определяют значения
3. Вычисляют 4. Вероятность того, что разность |x1-х2|>ε является случайной величиной, определяется равенством Р(|x1-х2|>ε)=1-Ptpn где tp=|x1-х2|/σ; n=n1+n2-2. Величина Р определяется по таблице Стьюдента. Если полученная вероятность Р>0,95, то разность |x1-х2| носит систематический характер.
Пример. Расчетные значения составили tp=3 и n=15. По таблице Стьюдента находим, что при n-1=14 и tp=2,98≡3 величина Р=0,99. Тогда Р= 0,99 > 0,95, что свидетельствует о систематическом характере погрешности.
В отличие от случайной погрешности, выявленной в целом в, зависимости от ее источников, систематическая погрешность рассматривается по составляющим в зависимости от источников ее возникновения, причем различают методическую, инструментальную и субъективную составляющие погрешности. Целесообразность разделения систематической погрешности на методическую и инструментальную составляющие определяется следующими моментами: • для повышения точности измерений можно выделить лимитирующие факторы, а следовательно, принять решение об усовершенствовании методики или выборе более точных СИ; • появляется возможность определить составляющую общей погрешности, увеличивающейся со временем или под влиянием внешних факторов, а следовательно, целенаправленно осуществлять периодические поверки и аттестации; • инструментальная составляющая может быть оценена до разработки методики, а потенциальные точностные возможности выбранного метода определит только методическая составляющая. То есть все виды составляющих погрешности нужно анализировать и выявлять в отдельности, а затем суммировать их в зависимости от характера, что является основной задачей при разработке и аттестации методик выполнения измерений. В ряде случаев систематическая погрешность может быть исключена за счет устранения источников погрешности до начала измерений (профилактика погрешности), а в процессе измерений — путем внесения известных поправок в результаты измерений. Профилактика погрешности — наиболее рациональный способ ее снижения и заключается в устранении влияния, например температуры (термостатированием и термоизоляцией), магнитных полей (магнитными экранами), вибраций и т. п. Сюда же относятся регулировка, ремонт и поверка СИ. Исключение постоянных систематических погрешностей в процессе измерений осуществляют методом сравнения (замещения, противопоставления), компенсации по знаку (предусматривают два наблюдения, чтобы в результат каждого измерения систематическая погрешность входила с разным знаком), а исключение переменных и прогрессирующих — способами симметричных наблюдений или наблюдением четное число раз через полупериоды.
|
|
 был существенно меньше Δси.
был существенно меньше Δси.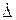 <Δс/2 до
<Δс/2 до 
 . (18)
. (18) .
. или
или 
 , так и среднего значения
, так и среднего значения  .
.
 .
.