|
|
Классы точности средств измерений.Приведенная в предыдущем параграфе номенклатура MX в местном смысле предполагает строгое нормирование MX СИ, используемых при высокоточных лабораторных измерениях и метрологической аттестации других СИ. При технических измерениях, когда не предусмотрено выделение случайных и систематических составляющих, когда не существенна динамическая погрешность СИ, когда не учитываются влияющие (дестабилизирующие) факторы и т.д., можно пользоваться более грубым нормированием — присвоением СИ определенного класса точности по ГОСТ 8.401—80. Класс точности — это обобщенная MX, определяющая различные свойства СИ. Например, у показывающих электроизмерительных приборов класс точности помимо основной погрешности включает также вариацию показаний, а у мер электрических величин — величину нестабильности (процентное изменение значения меры в течение года). Класс точности СИ уже включает систематическую и случайную погрешности. Однако он не является непосредственной характеристикой точности измерений, выполняемых с помощью этих СИ, поскольку точность измерения зависит и от метода измерения, взаимодействия СИ с объектом, условий измерения и т.д. В частности, чтобы измерить величину с точностью до 1%, недостаточно выбрать СИ с погрешностью 1%. Выбранное СИ должно обладать гораздо меньшей погрешностью, так как нужно учесть как минимум еще погрешность метода. В связи с большим разнообразием как самих СИ, так и их MX, ГОСТ 8.401—80 устанавливает несколько способов назначения классов точности. При этом в основу заложены следующие положения:
Определяя класс точности, нормируют прежде всего пределы допускаемой основной погрешности δосн. Пределы допускаемой дополнительной погрешности устанавливают в виде дольного (кратного) значения [δосн]. Классы точности присваивают СИ при их разработке по результатам государственных приемочных испытаний. Если СИ предназначены для измерения одной и той же физической величины, но в разных диапазонах, или — для измерения разных физических величин, то этим СИ могут присваиваться разные классы точности как по диапазонам, так и по измеряемым физическим величинам. В эксплуатации СИ должны соответствовать этим классам точности. Однако при наличии соответствующих эксплуатационных требований класс точности, присвоенный на производстве, в эксплуатации может понижаться. ГОСТ 8.401—80 в качестве основных устанавливает три вида классов точности СИ: • для пределов допускаемой абсолютной погрешности в единицах измеряемой величины или делениях шкалы; • для пределов допускаемой относительной погрешности в виде ряда чисел δ = ±А·10n где А= 1; 1.5; (1.6); 2; 2.5; (3); 4; 5 и 6; значения 1.6 и 3 —допускаемые, но не рекомендуемые; n= 1; 0; -1; -2;...; • для пределов допускаемой приведенной погрешности с тем же рядом А: γ = ±А·10n. Классы точности СИ, выраженные через абсолютные погрешности, обозначают прописными буквами латинского алфавита или римскими цифрами. При этом чем дальше буква от начала алфавита, тем больше значения допускаемой абсолютной погрешности. Например, СИ класса С более точен, чем СИ класса М, т. е. это число — условное обозначение и не определяет значение погрешности. Класс точности через относительную погрешность СИ назначается двумя способами.
Так обозначают классы точности мостов переменного тока, счетчиков электроэнергии, делителей напряжения, измерительных трансформаторов и др.
Здесь с и d выражаются также через ряд A. Причем, как правило, c>d. Например, класс точности 0,02/0,01 означает, что с=0,02, а d=0,01, т. е. приведенное значение относительной погрешности к началу диапазона измерения γн = 0,02%, а к концу — γк= 0,01%. Кроме того, ГОСТ 22261—94 устанавливает пределы допускаемой основной погрешности в виде относительной погрешности, выраженной в децибелах (дБ): δ = Aʹ·lg(l + Δ/x), где А'= 10 при измерении энергетических величин (мощности, энергии, плотности энергии); А'= 20 при измерении силовых электромагнитных величин (напряжения, силы тока, напряженности поля). Следует иметь в виду, что если два прибора имеют разные чувствительности S1=-100дБ/Вт и S2=-95 дБ/Вт, то значение чувствительности у второго СИ выше, чем у первого, так как -95> -100. Наиболее широкое распространение (особенно для аналоговых СИ) получило нормирование класса точности по приведенной погрешности:
Условное обозначение класса точности в этом случае зависит от нормирующего значения хN, т. е. от шкалы СИ. Если xN представляется в единицах измеряемой величины, то класс точности обозначается числом, совпадающим с пределом допускаемой приведенной погрешности. Например, класс 1,5 означает, что γ = 1,5%. Если xN — длина шкалы (например, у амперметров), то класс 1.5 означает, что γ =1,5% длины шкалы. Сравнения способов выражения погрешностей позволяет высказать некоторые соображения. При известном классе точности СИ, выраженном через приведенную погрешность γ и чувствительность S (отношение длины шкалы прибора к его диапазону измерения) абсолютная погрешность СИ составит Δ=γxN/100S, (1) а относительная на отметке х, соответственно, δ= γxN/xS. (2) При форме записи
Расчетные коэффициенты с и d округляются до принятых рядом А, а соотношение их с классом точности по приведенной погрешности γ приведено в следующей таблице: Таблица соотношения классов точности γ и коэффициентов c/d
Таблица формул вычисления погрешностей и обозначение классов точности СИ
Из формулы относительной погрешности δ=Δ/х видно, что ее значение растет обратно пропорционально х и изменяется по гиперболе, т. е. относительная погрешность равна классу СИ δ0 лишь на последней отметке шкалы (х = xк. При х→0 величина δ→∞. При уменьшении измеряемой величины до значения xmin относительная погрешность достигает 100%. Такое значение измеряемой величины называется порогом чувствительности. Резюмируя изложенное, следует сказать, что если класс точности СИ установлен по наибольшему допускаемому приведенному значению погрешности а для оценки погрешности конкретного измерения необходимо знать значение абсолютной или относительной погрешности в данной точке, то в этом случае выбор СИ, например, класс 1 (γ = 1%) для измерения с относительной погрешностью ±1% будет правильным, если верхний предел xN СИ равен измеряемому значению х величины. В остальных случаях относительную погрешность измерения необходимо определять по формуле
Пример.Отсчет по шкале прибора с пределами измерений 0 — 50 А и равномерной шкалой составил 25А. Пренебрегая другими видами погрешностей измерения, оценить пределы допускаемой абсолютной погрешности этого отсчета при использовании различных СИ класса точности: 0,02/0,01; (0.5 в кружочке) и 0,5. Решение.
так как х = 25; хк = 50; с =0,02; d = 0,01 и δ - в %, то Δ = ±[0.02 + 0.01(50/25-1) 25 0.01] = ±0,008А.
δ = ±Δ/х·100% ; Δ = ±0,01·25·0,5 =±0,185 А.
γ = ±Δ/хN·100%,где хN=50, тогда Δ = ±0,01·50·0,05 = ±0,25 А. Выбор средств измерений Лекция 5. |
|
 q
q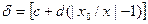
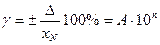
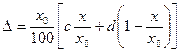 (3)
(3)
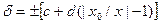


 (4)
(4)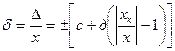 ,
,