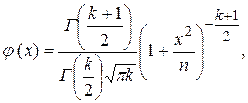Принципы описания и оценивания

Погрешностей

В основе современных подходов к оцениванию погрешностей лежат принципы, обеспечивающие выполнение требований единства измерений.

Единство измерений (traceability) – состояние измерений, характеризующееся тем, что их результаты выражаются в узаконенных единицах, а погрешности результатов известны и с заданной вероятностью не выходят за установленные пределы измерений.

Для исследования и оценивания погрешность описывается с помощью определенной модели (систематическая, случайная, методическая, инструментальная и др.). На выбранной модели определяют характеристики, пригодные для количественного выражения тех или иных свойств.

Выбор модели погрешности обусловлен сведениями об ее источниках как априорными, так и полученными в ходе измерительного эксперимента.

Систематическая погрешность по определению может быть представлена постоянной величиной, либо известной зависимостью (линейная, периодическая или другая функция). Общей моделью случайной погрешности служит случайная величина, обладающая функцией распределения вероятностей.

Характеристики случайной погрешности делят на точечные и интервальные. Для описания погрешностей результата измерений чаще всего используют интервальные оценки. Это значит, что границы, в которых может находиться погрешность, находят как отвечающие некоторой вероятности. В этом случае границы погрешности называют доверительными границами, а вероятность, соответствующую доверительной погрешности, доверительной вероятностью.

В целях единообразия представления результатов и погрешностей измерения показатели точности и формы представления результатов измерений стандартизованы.

Стандартом установлено, что в численных показателях измерений (в том числе и в погрешности) должно быть не более двух значащих цифр.

При записи результатов измерений наименьшие разряды числовых значений результата измерения и численных показателей точности должны быть одинаковы. Например, если оценка точности 0,53 мм, то результат измерения составляет 20,84 мм, или оценка точности 0,5 мм, тогда результат - 20,8 мм.

Практикой выработаны следующие правила округления результатов измерений:

- погрешность результата измерения указывается одной или двумя значащими цифрами. Две значащие цифры обязательны для выполнения точных измерений;

- результат измерения округляется так, чтобы он оканчивался цифрой того же разряда, что и значение погрешности, например, при погрешности ± 0,06 результат 12,124 будет записан как 12,12, а при ± 0,5 как 12,1;

- если числовое значение результата измерений представляется десятичной дробью, оканчивающейся нулями, то нули отбрасываются только до того разряда, который соответствует разряду числового значения погрешности, например: результат 35,000 при значении погрешности ± 0,06 записывается в виде 35,00, а при ± 0,5 в виде 35,0;

- если цифра старшего из отбрасываемых разрядов меньше 5, то оставшиеся цифры числа не меняются, например при результате 9,443 после округления записывается 9,4;

- если цифра старшего из отбрасываемых разрядов больше или равна 5, но за ней следуют отличные от нуля цифры, то последнюю оставляемую цифру увеличивают на единицу, например при сохранении трех значащих цифр число 28598 округляют до 28600;

- если отбрасываемая цифра равна 5, а следующие за ней цифры известны или нули, то последнюю сохраняемую цифру не изменяют, если она четная и увеличивают, если она нечетная, например 22,5 при сохранении двух значащих цифр округляют до 22, а число 23,5 – до 24;

- округление делают лишь в окончательном ответе, а все предварительные вычисления проводят с одним-двумя лишними знаками.

Источниками систематических составляющих погрешности измерения могут быть все его компоненты: метод измерения, средства измерения и экспериментатор. Оценивание систематических составляющих представляет достаточно трудную метрологическую задачу. Важность ее определяется тем, что знание систематической погрешности позволяет ввести соответствующую поправку в результат измерения и тем самым повысить его точность. Трудность же заключается в сложности обнаружения систематической погрешности, поскольку она не может быть выявлена путем повторных наблюдений. Проблема обнаружения систематических погрешностей едва ли не самая главная в борьбе с ними.

Постоянные инструментальные систематические погрешности обычно выявляют посредством поверки средства измерения. Поверка проводится сравнением показаний поверяемого прибора с показаниями более точного (образцового) средства измерения.

В метрологии установлено 12 областей измерения физических величин: измерения геометрических величин, измерения механических величин, измерения давления и вакуума; теплофизические и температурные измерения, измерения времени и частоты; измерения электрических и магнитных величин, измерение акустических величин и др. Практически во всех этих областях измерения встречаются случайные погрешности.

Случайные погрешности. Вероятностное описание

Отличающиеся друг от друга результаты измерений, проведенные с одинаковой тщательностью и в одинаковых условиях повторных наблюдений одной и той же постоянной величины, свидетельствуют о наличии в них случайных погрешностей. Каждая такая погрешность возникает вследствие одновременного воздействия на результат наблюдения многих случайных возмущений и сама является случайной величиной. В этом случае предсказать результат отдельного наблюдения и исправить его введением поправки невозможно. Можно лишь с определенной долей уверенности утверждать, что истинное значение измеряемой величины находится в пределах разброса результатов от х_min до х_max. Однако остается неясным, какова вероятность появления того или иного значения погрешности.

Равномерное распределение

Интегральное выражение функции распределения:

.

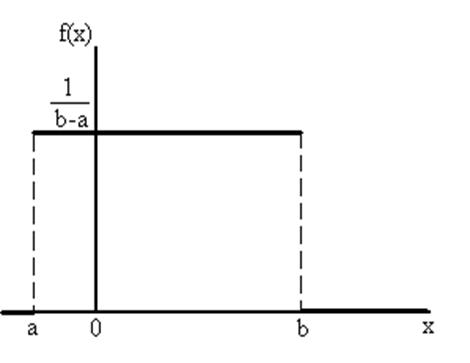
Дифференциальное выражение функции распределения (рис. 12):

, .

Основные характеристики равномерного распределения:

- математическое ожидание:

,

- дисперсия:

,

- среднеквадратичное отклонение:

,

- коэффициент вариации:

.

Рис. 12 Равномерное распределение случайной величины

Нормальное распределение

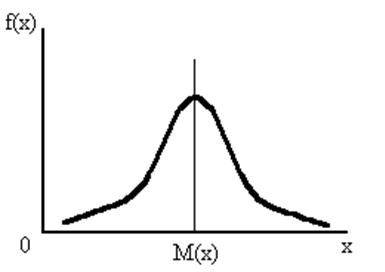
Нормальное распределение задаётся интегральной функцией или плотностью распределения (дифференциальной функцией распределения) (рис. 13):

;

.

Для нормального распределения основные характеристики равны:

, , .

Рис. 13. Нормальное распределение случайной величины

Основные характеристики нормального распределения:

- математическое ожидание:

,

- дисперсия:

,

- среднеквадратичное отклонение:

- коэффициент вариации:

.

Распределение Стьюдента

Распределением Стъюдента (t-распределение) называется распределение случайной величины t:

,

где Z – случайная величина, распределенная по стандартому нормальному закону.

х²– независимая от Z случайная величина, имеющая распределение с k степенями свободы.

Плотность вероятности распределения Стъюдента имеет вид (рис. 14):

Рис.14. Кривая распределения Стъюдента

Кривая распределения Стъдента симметрична относительно оси ординат, но по сравнению с нормальной кривой более пологая.

При k → ∞ t-распределение приближается к нормальному. Практически уже при при k > 30 можно считать t-распределение приближенно нормальным.

Математическое ожидание случайной величины, имеющей t-распре-деление, в силу симметрии ее кривой распределения равно нулю:

M (t) = 0.

Дисперсия t-распределения равна: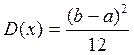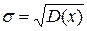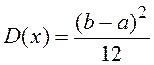