|
|
Прямые многократные измерения.Обработка данных
Способы нахождения оценок результата измерений зависят от вида функции распределения погрешностей и от имеющихся соглашений по этому вопросу, регламентируемых в рамках законодательной метрологии. Общие соображения по выбору оценок заключаются в следующем. Распределение погрешностей результатов наблюдений, как правило, являются симметричными относительно центра распределения, поэтому истинное значение измеряемой величины может быть определено как координата центра рассеивания xo, то есть центра симметрии распределения случайной величины (при условии, что систематическая погрешность исключена). Отсюда следует принятое в метрологии правило оценивания случайной погрешности в виде интервала симметричного относительно результата измерения. Правила обработки результатов измерений с многократными наблюдениями учитывают следующие факторы: - обрабатывается ограниченная группа из п наблюдений; - результаты наблюдений xi могут содержать систематическую погрешность; - в группе наблюдений могут встречаться грубые погрешности; - распределение случайных погрешностей может отличаться от нормального. Результаты наблюдений обрабатываются в следующей последовательности: 1) исключить известные систематические погрешности из результатов наблюдений (введением поправки); 2) вычислить среднее арифметическое исправленных результатов наблюдений, принимаемое за результат измерения:
3) вычислить оценку среднего квадратичного отклонения результатов наблюдений:
Вычислив σ целесообразно проверить наличие в группе наблюдений грубых погрешностей, помня, что при нормальном законе распределения ни одна случайная погрешность 4) вычислить оценку среднеквадратичного отклонения результата измерения Sx:
5) проверить гипотезу о том, что результаты наблюдений при-надлежат нормальному распределению. При числе наблюдений n < 15 принадлежность к нормальному закону не проверяют, а доверительные границы случайной погрешности результата определяют лишь в том случае, если достоверно известно, что результаты наблюдений принадлежат нормальному закону; 6) вычислить доверительные границы ε случайной погрешности результата измерения при заданной вероятности Р: где 7) при наличии систематических случайных погрешностей необходимо вычислить границы суммарной неисключенной систематической погрешности результата измерений. Неисключенная систематическая погрешность результата образуется из неисключенных систематических погрешностей метода, средств измерений, погрешностей поправок и других факторов При суммировании эти составляющие рассматриваются как случайные величины. При отсутствии данных о виде распределения неисключенных погрешностей их распределения принимают за равномерные. В этом случае границы неисключенной систематической погрешности результата измерения q вычисляют по формуле:
где q – граница i-й неисключенной составляющей систематической погрешности; k – коэффициент, определяемый принятой доверительной вероятностью; m – количество несключенных составляющих систематической погрешности; 8) вычислить доверительные границы погрешности результата измерения при наличии случайных и систематической погрешностей измерения. Анализ соотношения q /Sx показывает, что если q /Sx < 0,8, то неисключенной систематической погрешностью можно пренебречь и принять границы погрешности результата измерения равным ± ε. Если q / Sx > 8, то случайной погрешностью можно пренебречь и принять границы погрешности результата равными ± q. Если 0,8 < q /Sx < 8, вычисляют среднеквадратичное отклонение результата как сумму неисключенной систематической погрешности и случайной составляющей:
Границы погрешности результата измерения в этом случае вычисляют по формуле Δ =± K Sτ. Коэффициент K вычисляют по эмпирической формуле Пример-задание. Определить границы доверительного интервала для полученных результатов измерений. Было проведено 10 измерений диаметра и получены следующие результаты: 29,98; 29,99; 29,98; 29,96; 30,01; 30,03; 29,97; 29,98; 30,00; 29,99 (мм). Измерения проводились микрометром МК 25-50 при нормальных условиях. Систематические погрешности исключались настройкой микрометра на 0 перед началом измерений и после 5 измерений. Микрометр поверен. Выполним обработку данных: 1) систематические погрешности исключены в процессе измерения; 2) Вычислим среднее арифметическое результатов измерений:
Таблица 5 Данные для определения доверительного интервала
3) вычислим среднеквадратичное отклонение:
Проверим наличие грубых погрешностей: так как неравенство 3σ > (xi-X) выполняется при п=1, 2, 3, 4,...9, 10, грубых погрешностей нет;
4) определим оценку среднеквадратичного отклонения:
5) вычислим доверительные границы ε случайной погрешности результата измерений при заданной доверительной вероятности. Доверительную вероятность определяем с использованием прил. 2:
Доверительная вероятность Р = 0,75 » 0,8. Доверительные границы Используя прил. 3, определим tg = 1,38; e =1,38×0,0607 = 0,0838. Результаты измерения 29,989 ± 0,084. Используя правила округления, получаем (см. разд. 3.2), полученный результат измерения: 29,99 ± 0,08.
|
|

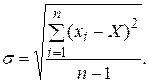
 ,с вероятностью практически равной единице, не может выйти за пределы ±3σ. Наблюдения, содержащие отклонения, превышающие 3σ, исключают из группы и заново повторяют вычисления x и σ в соответствии с пп. 2 и 3.
,с вероятностью практически равной единице, не может выйти за пределы ±3σ. Наблюдения, содержащие отклонения, превышающие 3σ, исключают из группы и заново повторяют вычисления x и σ в соответствии с пп. 2 и 3. ;
;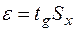 ,
,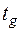 – коэффициент Стюдента;
– коэффициент Стюдента;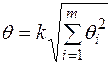 ,
,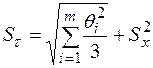 .
. .
.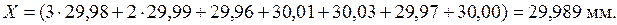 Исходные данные и результаты вычислений занесем в табл. 5.
Исходные данные и результаты вычислений занесем в табл. 5.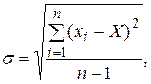
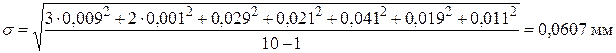
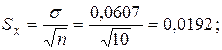
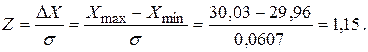
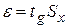 .
.