|
|
Тема 3.1.3 Абсолютные и относительные величины
Приступая к изучению данной темы, учащийся должен уяснить, что абсолютные величины - количественные обобщающие показатели, которые выражают размеры, объемы и уровни общественных явлений. Абсолютные величины являются именованными и могут быть выражены в натуральных и стоимостных единицах измерения. Относительными величинамив статистике называются обобщающие показатели, рассчитываемые как отношение двух абсолютных величин. Относительные величины выражаются в форме коэффициентов, процентов (%), промилле (%о), продецимилле (%оо). Относительные величины могут иметь также сложно - натуральную единицу измерения. Например, плотность населения характеризуется количеством человек на один квадратный километр территории. По характеру, назначению и сущности выражаемых количественных отношений различают следующие виды относительных величин: 1. Относительные величины планового задания - отношение планового задания данного периода к фактическому уровню предыдущего периода. 2. Относительные величины выполнения планового задания - отношение фактического уровня к плановому заданию одного итого же периода. 3. Относительные величины динамики - отношение одного и того же показателя за различные периоды времени. 4. Относительные величины сравнения - отношение одного и того же показателя за один и тот же момент времени, но по разным территориям или различным объектам. 5. Относительные величины структуры характеризуют состав изучаемой совокупности и представляют собой отношение частей целого к итогу. 6. Относительные величины координации характеризуют отношение отдельных частей целого друг к другу. 7. Относительные величины интенсивности характеризуют степень распространения явления в определенной среде или по отношению к другому показателю.
Литература: [4] c. 24-26; [5] c. 288-291; [8] c. 33-37.
Контрольные вопросы 1. Раскрыть понятие абсолютных величин и их значения в статистических исследованиях. 2. Перечислить единицы измерения абсолютных величин. 3. Что следует понимать под относительной величиной в статистике ? 4. Назвать виды относительных величин по характеру, назначению и сущности выражаемых количественных отношений. 5. Охарактеризовать порядок расчета относительных величин планового задания и выполнения планового задания. 6. Раскрыть понятие относительной величины динамики и порядка их расчета. 7. Какова сущность относительной величины сравнения ? 8. Дать характеристику относительной величины структуры, координации и интенсивности, охарактеризовать порядок их расчета. Тема 3.1.4 Средние величины и показатели вариации При изучении данной темы следует иметь в виду, что общественные явления, несмотря на наличие многочисленных и разнообразных уровней или значений, обладают некоторыми характерными свойственными большинству из них свойствами, которые могут выражаться в статистике при помощи средних величин. Средние величины в статистике - это показатели, выражающие характерные, свойственные большинству признаков размеры и соотношения. В статистике используются различные виды средних величин: средняя арифметическая, средняя гармоническая, средняя квадратическая, средняя хронологическая и т.д. Самой распространенной средней, используемой в социально-экономическом анализе, является средняя арифметическая. Она бывает простая и взвешенная. Средняя арифметическая простая рассчитывается по формуле:
где х – индивидуальные значения признака, средняя величина которых находится; n – количество единиц совокупности. Если же варианты (значения признака) встречаются неодинаковое число раз, то используется средняя арифметическая взвешенная:
где х – варианты, значения признака; f - частота появления соответствующего значения признака. Средняя гармоническая взвешенная является преобразованием среднеарифметической и применяется в тех случаях, когда необходимые частоты не заданы. Если известны варианты значений признака (Х), и ряд произведений вариант на частоту
Мода – величина признака (варианта), которая встречается в ряду распределения с наибольшей частотой (весом). Медиана – величина признака у единицы, находящейся в середине ранжированного (упорядоченного) ряда.
В интервальном вариационном ряду мода и медиана исчисляются на основе следующих формул:
где Мо и Ме – соответственно моде и медиане; Хо – нижняя граница модального (медианного интервала); Í – величина модального (медианного) интервала; fm – частота модального (медианного) интервала; fm + 1 – частота интервала, следующего за модальным; åf – сумма частот ряда; Sm – 1 – сумма частот в интервалах, предшествующих медианному. В ходе изучения статистических явлений и процессов общественной жизни обычно имеются разнообразные варианты, значения признаков. Вариация – изменение (колеблемость) значений признака внутри совокупности. Величины признаков варьируют под воздействием различных причин и условий. Чем разнообразнее условия, влияющие на размер данного признака тем больше его вариация. Показатели вариации: · размах вариации – R · среднее линейное отклонение - · дисперсия признака- · среднее квадратическое отклонение - · коэффициент вариации -
1.Размах вариации – разность между максимальным и минимальным значениями признака в изучаемой совокупности
2. Среднее линейное отклонение- средняя величина из отклонений индивидуальных значений признака от средней арифметической. Поскольку сумма всех отклонений от средней равна нулю, разности берутся по модулю. Для несгруппированных данных
Для сгруппированных данных
3.Дисперсия признака – средний квадрат отклонений индивидуальных значений признака от средней величины. Для несгруппированных данных
Для сгруппированных данных
4.Среднее квадратическое отклонение- корень квадратный из среднего квадрата отклонений индивидуальных значений признака от средней величины.
5. Коэффициент вариации- отношение среднего квадратического отклонения к средней арифметической
Литература: [4] c. 31-38; [5] c. 291-298; [8] c. 38-58.
Контрольные вопросы 1. Охарактеризовать понятие средних величин и правила их применения. 2. Раскрыть назначение средней арифметической и средней хронологической. 3. Перечислить характеристики средней гармонической взвешенной и простой, и условия их применения. 4. Охарактеризовать назначение моды и медианы в статистике как структурных средних. 5. Перечислить формулы расчета моды и медианы для интервального вариационного ряда. 6. Дать понятие вариации признаков и порядка их применения. 7. Раскрыть назначение абсолютных и относительных показателей вариации и порядок их расчета.
Тема 3.1.5 Ряды динамики Приступая к изучению данной темы, учащийся должен уяснить, что ряды динамики позволяют измерить динамику изучаемых явлений на основе системы статистических показателей, выявить и количественно оценить основную тенденцию развития изучаемого явления, исследовать сезонные колебания в развитии явлений и процессов общественной жизни, и также произвести прогнозирование уровней социально-экономических явлений. Динамические ряды- ряды числовых показателей, характеризующих изменения явлений во времени. Они состоят из двух показателей: периода времени t и уровня ряда y. Правила построения динамических рядов: - уровни должны иметь одни единицы измерения; - показатели должны быть территориально сопоставимы; - показатели должны быть сопоставимы по методологии расчета.
Виды динамических рядов - моментные и интервальные. Моментныединамические ряды - характеризуют состояние явлений на определенный момент времени. Уровни моментных рядов суммировать нельзя. Интервальные динамические ряды - характеризуют явления за определенный период времени. Уровни интервальных рядов можно суммировать. Динамические ряды, представленные абсолютными величинами, называют основными, а представленные относительными или средними величинами - производными. При изучении динамики социально - экономических явлений рассчитывают аналитические показатели: Абсолютный прирост (DУ): а) базисными (DУб), когда при определении приростов из текущих уровней ряда динамики (уí) вычитают уровень, принятый за базу сравнения (уо): DУб = Уí – Уо; б) цепными (DУц), когда при определении приростов из каждого текущего уровня ряда динамики (уí), вычитают предыдущий уровень (уí – 1): DУц = Уí – Уí – 1; Кроме того, можно рассчитать общий абсолютный прирост (DУ) для динамического ряда за весь анализируемый период: DУ = åDУц;
Относительные показатели предполагают соотношение уровней динамического ряда. В числе их могут быть:
Темпы роста (Т): а) базисные (Тб), рассчитываются отношением уровней динамического ряда текущего периода к уровню, принятому за базу сравнения:
б) цепные (Тц), определяют соотношение текущих и предшествующих им уровней динамического ряда:
Темпы прироста(∆Т):
а) базисные (∆Тб) б) цепные (∆Тц)
Абсолютное значение одного процента прироста Аị% - это отношение абсолютного прироста DУ, за определенный период к темпу прироста DТ за этот же период, выраженному в процентах:
Средние показатели ряда динамики: 1. Средний уровень ряда динамики (у): Для интервальных рядов с равноотстоящими уровнями применяется средняя арифметическая простая:
где у – уровень интервального ряда; n – количество равных периодов времени.
В интервальных рядах с неравноотстоящими уровнями используется средняя арифметическая взвешенная:
где t – периоды времени, отделяющие один уровень ряда от другого. Средний абсолютный прирост Средний абсолютный прирост (D`у) рассчитывается по средней арифметической простой цепных абсолютных приростов (Dуц) за последовательные и равные по продолжительности периоды:
где n – число уровней ряда динамики; n – 1 – число цепных абсолютных приростов.
3. Средний темп роста Рассчитывается по формуле средней геометрической цепных темпов роста, выраженных в коэффициентах.
где m = n – 1 – число цепных темпов роста.
4. Средний темп прироста Вычисляется как простая разность: D`Т = `Т – 1
Уровни социально-экономических явлений подвержены сезонным колебаниям, которые являются результатом влияния природных, общественных и экономических факторов. В статистике сезонные колебания характеризуются индексами сезонности, совокупность которых образует сезонную волну. Индекс сезоннасти (Jс) определяется по формуле:
Yi – уровни по месяцам; Месячные данные одного года недостаточны для выявления сезонных колебаний. Поэтому используются данные за несколько лет, в основном, за три года. Средний уровень рассчитывается на основании данных 36 месяцев.
Литература: [4] c. 45-53; [5] c. 308-332; [8] c. 70-91.
Контрольные вопросы 1. Раскрыть понятие и назначение рядов динамики. 2. Охарактеризовать виды динамических рядов и правила их построения. 3. Перечислить аналитические показатели ряда. 4. Дать характеристику средних показателей ряда динамики. 5. В чем состоит сущность сезонных колебаний. 6. Раскрыть понятие сезонной волны. 7. Охарактеризовать методы исчисления индексов сезонности.
Тема 3.1.6 Индексы
При изучении данной темы следует иметь в виду, что с помощью индексов изучается народное хозяйство в целом и его отдельные отрасли, а также деятельность предприятий, фирм, и др.; выявляется динамика развития социально- экономических явлений, анализируется выполнение планов или норм и др. Индексом в статистике называется относительный показатель, характеризующий соотношение во времени, по сравнению с планом или в пространстве уровней социально- экономических явлений. Индексы рассчитываются как для отдельных элементов сложного явления, так и для всего сложного явления в целом. В первом случае они называются индивидуальными и обозначаются i, а во втором - общими и обозначаются I. Для удобства построения индексов в статистике разработана следующая символика: q- количество единиц данного вида произведенной или реализованной продукции; p-цена единицы изделия; z-себестоимость единицы изделия; m-расход материала ( топлива) на единицу продукции и т.д.
Следовательно, индивидуальный индекс физического объема будет иметь вид:
Формула индивидуального индекса цен будет:
Индивидуального индекса себестоимости:
и т.д. Чтобы сделать сопоставимыми несоизмеримые явления (или их элементы), нужно выразить их общей мерой: стоимостью, трудовыми затратами и т.д. Эта задача решается построением и расчетом общих индексов. Основной формой общих индексов являются агрегатные индексы. Агрегатный индекс цен
Агрегатный индекс физического объема
Агрегатный индекс стоимости продукции (товарооборота)
Взаимосвязь индексов может быть представлена выражением:
Используя эти формулы, можно по двум известным индексам определить третий. Например, если известны индексы общей стоимости и цен, то индекс физического объема находится делением первого индекса на второй:
Если известны индексы общей стоимости и физического объема, то индекс цен определяется как частное от деления первого индекса на второй: Ip=Ipq :Iq. Агрегатные индексы дают возможность определить не только относительные изменения явления, но и найти абсолютные значения изменений, если из числителя каждого агрегатного индекса вычесть его знаменатель, то получим величины абсолютных приростов. Для более глубокого изучения динамики экономических явлений, выявления закономерностей и тенденций их развития проводятся индексные сопоставления за ряд последовательных периодов. В этом случае рассчитывается система цепных и базисных индексов. Базисные индексы – система последовательно вычисленных индексов одного и того же явления, характеризующих его изменение по отношению к постоянной базе. Цепные индексы – система индексов одного и того же явления, показывающим изменение его по отношению к меняющейся базе.
Литература: [5] c. 332-337; [8] c. 91-113.
Контрольные вопросы 1. Раскрыть общее понятие об индексах и их видах, применяемых в статистических исследованиях. 2. Охарактеризовать принципы построения индивидуальных и общих индексов. 3. В чем состоят особенности агрегатной формы индексов? 4. Указать по каким формулам определяются агрегатные индексы: физического объема, цен и стоимости продукции (товарооборота)? 5. Охарактеризовать какими выражениями может быть представлена взаимосвязь агрегатных индексов. 6. Дать характеристику базисным индексам. 7. Раскрыть понятие и сущность цепных индексов. 8. Как использовать индексный метод при анализе взаимосвязи экономических явлений и процессов?
|
|


 , а сама частота
, а сама частота  неизвестна, то в этом случае рассчитывается по формуле средней гармонической взвешенной:
неизвестна, то в этом случае рассчитывается по формуле средней гармонической взвешенной:












 %
%



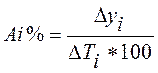






 ;
; - средний уровень ряд/
- средний уровень ряд/ ;
; ;
; ;
;




 , или
, или .
.