|
|
Доверительные интервалы для генеральной долиНорильский индустриальный институт Кафедра экономики и управления предприятием
Статистика
Методические указания к самостоятельной работе студентов экономических специальностей (всех форм обучения)
Норильск, 2003 г. Статистика. Методические указания к самостоятельной работе для студентов специальности 060800 ''Экономика и управление на предприятии (по отраслям)'', 061100 ''Менеджмент'', 060500 «Бухгалтерский учет, анализ и аудит», 060400 «Финансы и кредит».
Составители: Орел Ю. А., ст. преподаватель Смирнова А. Т., ст. преподаватель
Методические указания предназначены студентам специальностей 060800, 061100, 060500, 060400, всех форм обучения. Указания разработаны в соответствии с учебным планом, содержат основные теоретические положения, примеры решения типовых задач, а также задачи для самостоятельной работы.
© Норильский индустриальный институт, 2003
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ Статистическая сводка и группировка
Сводка представляет собой комплекс последовательных операций по обобщению конкретных единичных фактов, образующих совокупность, для выявления типичных черт и закономерностей, присущих изучаемому явлению в целом. По глубине обработки материала сводка бывает простая и сложная. Простой сводкой называется операция по подсчету общих итогов по совокупности единиц наблюдения. Сложная сводка представляет собой комплекс операций, включающих группировку единиц наблюдения, подсчет итогов по каждой группе и по всему объекту и представление результатов группировки и сводки в виде статистических таблиц. Группировкой называется расчленение множества единиц изучаемой совокупности на группы по определенным существенным для них признакам. Группировки являются важнейшим статистическим методом обобщения данных, основой для правильного исчисления статистических показателей. С помощью метода группировок решаются следующие задачи: q разделение всей совокупности на качественно однородные групп - выделения социально-экономических типов. Эти группировки называются типологическими (например, группировка хозяйственных объектов по формам собственности, населения по общественным группам и др.). q характеристика структуры явления и структурных сдвигов, происходящих в нем. Эти группировки называются структурными(например, изучение состава населения по полу, возрасту и другим признакам, характеристика предприятий по числу работающих и т.д.). q изучение взаимосвязи между отдельными признаками изучаемого явления. Такие группировки называются аналитическими или факторными (например, группировка предприятий определенной отрасли экономики по уровню производительности труда для выявления ее влияния на себестоимость продукции. Группировка банков по величине активов и др.) Метод группировки основывается на двух категориях — группировочном признаке и интервале. Группировочный признак — это признак, по которому происходит объединение отдельных единиц совокупности в однородные группы. Классификация и группировка должны производиться на основании вполне объективных и легко распознаваемых признаков. Группировка может производиться по одному признаку (простая группировка) и по нескольким признакам (комбинированная группировка). Интервал очерчивает количественные границы групп. Как правило, он представляет собой промежуток между максимальными и минимальными значениями признака в группе. Интервалы бывают: равные, когда разность между максимальным и минимальным значениями в каждом из интервалов одинакова; неравные, когда, например, ширина интервала постепенно увеличивается, а верхний интервал часто не закрывается вовсе; открытые, когда имеется только либо верхняя, либо нижняя граница; закрытые, когда имеются и нижняя, и верхняя границы. При проведении группировки решаются следующие вопросы. 1. Выбор группировочного признака. 2. Определение числа групп и величины интервала. Для нахождения числа групп служит формула: n = 1 + 3,322• lg N, где N — количество элементов совокупности. Для нахождения величины интервала существует формула:
где Средние величины
Средняя величина — это обобщающий показатель, характеризующий типичный уровень варьирующего количественного признака на единицу совокупности в определенных условиях места и времени. Объективность и типичность статистической средней обеспечивается лишь при определенных условиях. Первое условие - средняя должна вычисляться для качественно однородной совокупности. Для получения однородной совокупности необходима группировка данных, поэтому расчет средней должен сочетаться с методом группировок. Второе условие - для исчисления средних должны быть использованы массовые данные. В средней величине, исчисленной на основе данных о большом числе единиц (массовых данных), колебания в величине признака, вызванные случайными причинами, погашаются и проявляется общее свойство (типичный размер признака) для всей совокупности. Средняя величина всегда именованная, она имеет ту же размерность, что и признак у отдельных единиц совокупности. Средние величины делятся на два больших класса: степенные средние, структурные средние. Кстепенным средним относятся такие наиболее известные и часто применяемые виды, как средняя геометрическая, средняя арифметическая и средняя квадратическая. В качествеструктурных средних рассматриваются мода и медиана. Степенные средние в зависимости от представления исходных данных могут быть простыми и взвешенными. Простая средняя считается по несгруппированным данным и имеет следующий общий вид:
где хi - варианта (значение) определенного признака, m – показатель степени средней. n – число вариант (значений). Взвешенная средняя считается по сгруппированным данным и имеет вид:
где хi - варианта (значение) определенного признака или серединные значения интервала, в котором измеряется варианта, m – показатель степени средней. fi – частота, показывающая сколько раз встречается i-е значение осредняемого признака. Общие формулы расчета степенных средних имеют показатель степени (m). В зависимости от того, какое значение он принимает, различают следующие виды степенных средних: средняя гармоническая, если m = -1; средняя геометрическая, если m -> 0; средняя арифметическая, если m = 1; средняя квадратическая, если m = 2; средняя кубическая, если m = 3. Формулы степенных средних приведены в таблице 1.1.:
Структурные средние - мода и медиана - в отличие от степенных средних, которые в значительной степени являются абстрактной характеристикой совокупности, выступают как конкретные величины, совпадающие с вполне определенными вариантами совокупности. Это делает их незаменимыми при решении ряда практических задач. Модой называется значение признака, которое наиболее часто встречается в совокупности (в статистическом ряду). Медианой называется значение признака, которое лежит в середине ранжированного ряда и делит этот ряд на две равные по численности части. Для определения медианы сначала определяют ее место в ряду, используя формулу
где n - число членов ряда. Если ряд состоит из четного числа членов, то за медиану условно принимают среднюю арифметическую их двух срединных значений. В отличие от дискретных вариационных рядов определение моды и медианы по интервальным рядам требует проведения определенных расчетов на основе следующих формул:
где
Модальный интервал определяется по наибольшей частоте.
где
Показатели вариации
Конкретные условия, в которых находится каждый из изучаемых объектов, а также особенности их собственного развития (социальные, экономические и пр.) выражаются соответствующими числовыми уровнями статистических показателей. Таким образом, вариация, т.е. несовпадение уровней одного и того же показателя у разных объектов имеет объективный характер и помогает познать сущность изучаемого явления. Для измерения вариации в статистике применяют несколько способов. Размахвариации (R) показывает, насколько велико различие между единицами совокупности, имеющими самое маленькое и самое большое значение признака. Его рассчитывают как разность между наибольшим и наименьшим значениями варьирующего признака, т. е. R=Xmax-Xmin Однако размах вариации показывает лишь крайние значения признака. Повторяемость промежуточных значений здесь не учитывается. Более строгими характеристиками являются показатели колеблемости относительно среднего уровня признака. Простейший показатель такого типа – средне линейное отклонение. Оно вычисляется как средняя арифметическая из абсолютных значений отклонений вариант хi, и для несгруппированных данных где n – число членов ряда; для сгруппированных данных где Среднее линейное отклонение дает обобщенную характеристику степени колеблемости признака в совокупности. К сожалению, этот показатель усложняет расчеты вероятностного типа, затрудняет применение методов математической статистики. Поэтому в статистических научных исследованиях для измерения вариации чаще всего применяют показатель дисперсии. Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины и вычисляется по формулам простой и взвешенной дисперсий (в зависимости от исходных данных): простая дисперсия для несгруппированных данных взвешенная дисперсия для сгруппированных данных
Формула для расчета дисперсии может быть преобразована в Дисперсия есть средняя величина квадратов отклонений. Если извлечь корень из дисперсии получим среднее квадратическое отклонение: для несгруппированных данных для сгруппированных данных Среднее квадратическое отклонение - это обобщающая характеристика размеров вариации признака в совокупности. Оно выражается в тех же единицах измерения, что и признак (в метрах, тоннах, рублях, процентах и т. д.). До сих пор говорилось о показателях вариации, выраженных в абсолютных величинах. Но для целей сравнения колеблемости различных признаков в одной и той же совокупности или же при сравнении колеблемости одного и того же признака в нескольких совокупностях представляют интерес показатели вариации, приведенныев относительных величинах. Базой для сравнения должна служить средняя арифметическая. Эти показатели вычисляются как отношение размаха вариации, среднего линейного отклонения или среднего квадратического отклонения к средней арифметической или медиане. Чаще всего они выражаются в процентах и определяют не только сравнительную оценку вариации, но и дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному). Различают следующие относительные показатели вариации (V): Коэффициент осцилляции (
Линейный коэффициент вариации (
Коэффициент вариации (
Выяснение общего характера распределения предполагает оценку его однородности, а также вычисление показателей асимметрии и эксцесса. Для симметричных распределений частоты любых двух вариант, равноотстоящих в обе стороны от центра распределения, равны между собой. Рассчитанные для таких распределений средняя, мода и медиана также равны. При сравнительном изучении асимметрии нескольких распределений с разными единицами измерения вычисляется относительный показатель асимметрии ( Его величина может быть положительной и отрицательной. В первом случае речь идет о правосторонней асимметрии, а во втором - о левосторонней. Принято считать, что асимметрия выше 0,5 (независимо от знака) считается значительной; если она меньше 0,25, то незначительной. Для симметричных распределений может быть рассчитан показатель эксцесса (островершинности).
где
Эксцесс может быть положительным и отрицательным. У высоковершинных распределений показатель эксцесса имеет знак (+), а у низковершинных – знак (-). Предельным значением отрицательного эксцесса является величина Ех=-2; величина положительного эксцесса является величиной бесконечной. В нормальном распределении Ех=0.
Выборочное наблюдение
Выборочный метод применяется в тех случаях, когда проведение сплошного наблюдения невозможно или экономически нецелесообразно. Выборочное наблюдение используют также для проверки результатов сплошного наблюдения. Ту часть единиц, которые отобраны для наблюдения, принято называть выборочной совокупностью, а всю совокупность единиц, из которых производится отбор, — генеральной. Качество результатов выборочного наблюдения зависит от того, насколько состав выборки представляет генеральную совокупность, иначе говоря, от того, насколько выборка репрезентативна (представительна). Для обеспечения репрезентативности выборки необходимо соблюдение принципа случайности отбора единиц. Принцип случайности предполагает, что на включение или исключение объекта из выборки не может повлиять какой-либо иной фактор, кроме случая. Однако вычисленные по материалам выборочного наблюдения статистические показатели не будут точно совпадать с соответствующими характеристиками для всей совокупности (генеральной совокупности). Величина этих отклонений называется ошибкой наблюдения. Принятые условные обозначения: N - объем генеральной совокупности (число входящих в нее единиц); n - объем выборочной совокупности (число единиц, попавших в выборку); р - генеральная доля (доля единиц, обладающих данным признаком в генеральной совокупности); w - выборочная доля (доля единиц, обладающих данным признаком в выборочной совокупности);
S2 - выборочная дисперсия (дисперсия признака в выборочной совокупности); S - среднее квадратическое отклонение признака в выборочной совокупности.
При расчете ошибок возникает существенное затруднение: величины Таблица 1.2. Формулы ошибок простой случайной выборки
Формулы предельной ошибки позволяют решать задачи трех видов: 1. Определение пределов генеральных характеристиксзаданной степенью надежности (доверительной вероятностью) на основе показателей, полученных по данным выборки. Доверительные интервалы для генеральной средней:
Доверительные интервалы для генеральной доли
2. Определение доверительной вероятности того, что генеральная характеристика может отличаться от выборочной не более чем на определенную заданную величину. Доверительная вероятность является функцией от t, определяемой по формуле
По величине t определяется доверительная вероятность (смотрится по соответствующим таблицам). 3. Определение необходимого объема выборки, который практической вероятностью обеспечивает заданную точность выборки. Для расчета объема выборки необходимо иметь следующие данные: а) размер доверительной вероятности (Р), б) коэффициент t, зависящий от принятой вероятности; в) величину г) величину максимально допустимой ошибки ( д) объем генеральной совокупности. Необходимый объем выборки определяется на основе допустимой величины ошибки: В табл. 1.3 приведены формулы для расчета численности простой случайной выборки. Таблица 1.3. |
|
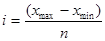 ,
, - соответственно минимальное и максимальное значение признака в совокупности.
- соответственно минимальное и максимальное значение признака в совокупности.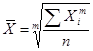

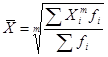
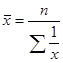
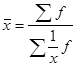
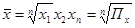
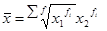


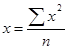

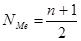
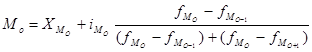 ,
, - нижняя граница модального интервала;
- нижняя граница модального интервала; - модальный интервал;
- модальный интервал;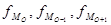 - частоты в модальном, предыдущем и следующем за модальным интервалах (соответственно).
- частоты в модальном, предыдущем и следующем за модальным интервалах (соответственно).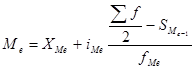 ,
, - нижняя граница медианного интервала;
- нижняя граница медианного интервала;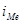 - медианный интервал;
- медианный интервал;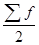 - половина от общего числа наблюдений (полусумма накопленных частот);
- половина от общего числа наблюдений (полусумма накопленных частот);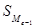 - сумма наблюдений, накопленная до начала медианного интервала;
- сумма наблюдений, накопленная до начала медианного интервала;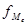 - число наблюдений в медианном интервале.
- число наблюдений в медианном интервале.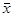 (взвешенная или простая в зависимости от исходных условий) по следующим формулам:
(взвешенная или простая в зависимости от исходных условий) по следующим формулам: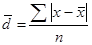 ,
,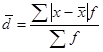 ,
,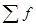 - сумма частот вариационного ряда.
- сумма частот вариационного ряда.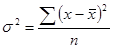 ,
,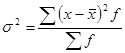 .
.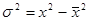 , т.е. дисперсия равна средней из квадратов индивидуальных значений признака минус квадрат средней величины.
, т.е. дисперсия равна средней из квадратов индивидуальных значений признака минус квадрат средней величины.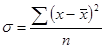 ,
,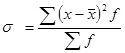 .
.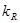 ):
):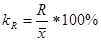
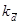 ):
):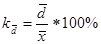
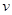 ):
):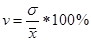
 ).
).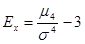 ,
,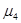 - центральный момент четвертого порядка;
- центральный момент четвертого порядка;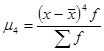
 - генеральная средняя (среднее значение признака в генеральной совокупности);
- генеральная средняя (среднее значение признака в генеральной совокупности);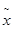 - выборочная средняя (среднее значение признака в выборочной совокупности);
- выборочная средняя (среднее значение признака в выборочной совокупности);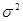 - генеральная дисперсия (дисперсия признака в генеральной совокупности);
- генеральная дисперсия (дисперсия признака в генеральной совокупности);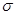 - среднее квадратическое отклонение признака в генеральной совокупности;
- среднее квадратическое отклонение признака в генеральной совокупности;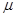 :
для средней
:
для средней
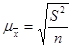
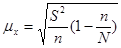
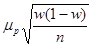
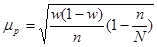
 для средней
для средней
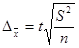


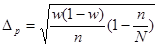
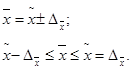
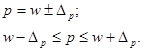
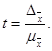
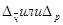 );
);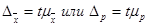 .
.