|
|
Корреляционно-регрессионный анализ
Корреляционная связь - связь, проявляющаяся не в каждом отдельном случае, а в массе случаев в средних величинах в форме тенденции. Статистическое исследование ставит своей конечной целью получение модели зависимости для ее практического использования. Решение этой задачи осуществляется в следующей последовательности. 1. Логический анализ сущности изучаемого явления и причинно-следственных связей. В результате устанавливаются результативный показатель (у), факторы его изменения, характеризуемые показателями (x1,x2,x3, ...,xn). Связь двух признаков (у и х) называетсяпарной корреляцией. Влияние нескольких факторов на результативный признак называетсямножественной корреляцией. По общему направлению связи могут быть прямые и обратные. При прямых связях с увеличением признака х увеличивается и признак у, при обратных - с увеличением признака х признак у уменьшается. 2. Сбор первичной информации и проверка ее на однородность и нормальность распределения. Для оценки однородности совокупности используется коэффициент вариации по факторным признакам. 3. Исключение из массива первичной информации всех резко выделяющихся (аномальных) единиц по уровню признаков-факторов. Исключаются все единицы, у которых уровень признака-фактора не попадает в интервал
и формируется новый массив для последующего анализа. 4. Установление факта наличия и направления корреляционной зависимости между результативным (у) и факторным (x) признаками. Основным методом выявления наличия корреляционной связи является метод аналитической группировки и определения групповых средних. Он заключается в том, что все единицы совокупности разбиваются на группы по величине признака-фактора и для каждой группы определяется средняя величина результативного признака. На основе данных аналитической группировки строится график эмпирической линии связи (линии регрессии), вид которой не только позволяет судить о возможном наличии связи, но и дает некоторое представление о форме корреляционной связи. Если эмпирическая линия связи по своему виду приближается к прямой линии, то можно предположить наличие прямолинейной корреляционной связи; если эмпирическая линия приближается к какой-либо кривой, то это связано с наличием криволинейной связи. 5. После установления факта наличия связи и ее формы измеряется степень тесноты связи и проводится оценка ее существенности. Для определения степени тесноты парной линейной зависимости служит линейный коэффициент корреляции (r); при любой форме зависимости (линейной и криволинейной) - эмпирическое корреляционное отношение (
где
n --- число единиц в совокупности;
Линейный коэффициент корреляции может принимать значения в пределах от -1 до +1. Чем ближе он по абсолютной величине к 1, тем теснее связь. Знак при нем указывает направление связи: знак «+» соответствует прямой зависимости, знак «-» - обратной. Корреляционное отношение изменяется от 0 до 1: чем ближе к 1, тем связь теснее; направление связи он не показывает, оно устанавливается по данным групповой таблицы. 6. После установления достаточной степени тесноты связи выполняется построение модели связи (уравнения регрессии). Тип модели выбирается на основе сочетания теоретического анализа и исследования эмпирических данных посредством построения эмпирической линии регрессии. Чаще всего используются следующие типы функций: а) линейная: б) гиперболическая: в) параболическая: г) показательная: Для определения численных значений параметров уравнения связи (линии регрессии) используется метод наименьших квадратов и решается система нормальных уравнений. Для определения параметров а и b уравнения прямолинейной корреляционной связи система нормальных уравнений (для несгруппированных данных) следующая:
Решение указанной системы уравнений дает следующие формулы для расчета параметров а и b:
7. Изучение множественной корреляционной зависимости начинается с анализа матрицы парных коэффициентов корреляции, что позволяет произвести отбор факторов, включаемых в модель множественной зависимости. Матрица имеет следующий вид:
Анализ первой строки матрицы позволяет выявить факторы, у которых степень тесноты связи с результативным показателем значительна, а поэтому они могут быть включены в модель. Однако при построении многофакторных моделей должно соблюдаться требование возможно меньшей коррелированности включенных в модель признаков-факторов (отсутствие мультиколлинеарности). В качестве критерия мультиколлинеарности может быть принято соблюдение следующих неравенств:
Если приведенные неравенства (или хотя бы одно из них) не выполняются, то исключается тот фактор хj, или xk, связь которого с результативным признаком у будет менее тесной. 8. Отобранные факторы включаются в модель множественной зависимости. При этом следует учитывать, что число факторов, включаемых в модель, должно быть в 5 - 6 раз меньше, чем число единиц, входящих в совокупность. Линейное уравнение множественной зависимости имеет следующий вид:
9. Для измерения степени тесноты связи между изменениями величины результативного признака (у) и изменениями значений факторных признаков определяется коэффициент множественной (совокупной) корреляции (R). Для случая зависимости результативного признака от двух факторных признаков формула совокупного коэффициента корреляции имеет вид:
Величина R2 называется еще коэффициентом детерминации; она показывает, в какой мере вариация результативного признака обусловлена влиянием признаков-факторов, включенных в уравнение множественной зависимости. Величина совокупного коэффициента корреляции изменяется в пределах от 0 до 1 и численно не может быть меньше, чем любой из образующих его парных коэффициентов корреляции. Чем ближе он к единице, тем меньше роль неучтенных в модели факторов и тем более оснований считать, что параметры регрессионной модели отражают степень эффективности включенных в нее факторов. Кроме совокупного коэффициента корреляции познавательное значение имеют частные коэффициенты корреляции, позволяющие установить степень тесноты связи между результативным признаком у и каждым из факторных признаков при исключении искажающего влияния других факторных признаков. Следовательно, коэффициенты частной корреляции отражают степень «чистого» влияния факторного признака на результативный признак. Для их расчета могут быть использованы парные коэффициенты корреляции. Для случая зависимости результативного признака y от двух признаков-факторов (x1 и x2)определяются два коэффициента частной корреляции: • частный коэффициент корреляции между результативным признаком y и фактором х при элиминировании фактора x1:
• частный коэффициент корреляции между результативным признаком у и фактором x2 при элиминировании фактора x1:
Для общего случая частные коэффициенты корреляции определяются по формуле
где
Величина частного коэффициента корреляции лежит в пределах от 0 до 1, а знак определяется знаком соответствующих параметров регрессии. Рассчитывая величины частных коэффициентов корреляции, следует иметь в виду, что каждый из них по своей абсолютной величине не может быть больше величины коэффициента множественной (совокупной) корреляции
|
|
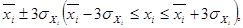
 ). Формулы их расчета для несгруппированных данных следующие:
). Формулы их расчета для несгруппированных данных следующие: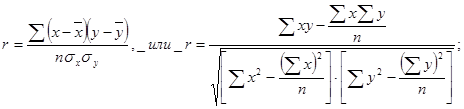
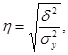
 --- отклонения вариантов значений признака-фактора от их средней величины;
--- отклонения вариантов значений признака-фактора от их средней величины;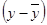 --- отклонения вариантов значений результативного признака от их средней величины;
--- отклонения вариантов значений результативного признака от их средней величины; --- среднее квадратическое отклонение соответственно признака-фактора и результативного признака;
--- среднее квадратическое отклонение соответственно признака-фактора и результативного признака; --- межгрупповая дисперсия результативного признака, вызванная влиянием признака-фактора.
--- межгрупповая дисперсия результативного признака, вызванная влиянием признака-фактора. ;
;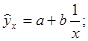
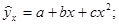
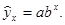
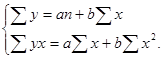
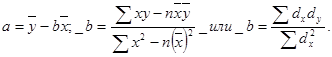






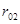



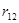

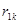

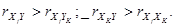
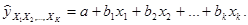
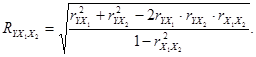
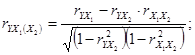
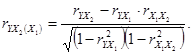
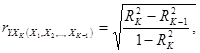
 --- коэффициент детерминации результативного признака yс комплексом факторных признаков x1, x2,…, x k-1, xk;
--- коэффициент детерминации результативного признака yс комплексом факторных признаков x1, x2,…, x k-1, xk;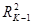 --- коэффициент детерминации результативного признака с комплексом признаков x1, x2,…, x k-1;
--- коэффициент детерминации результативного признака с комплексом признаков x1, x2,…, x k-1; --- частный коэффициент корреляции результативного признака y с факторным признаком xk при исключении влияния факторных признаков x1, x2,…, x k-1.
--- частный коэффициент корреляции результативного признака y с факторным признаком xk при исключении влияния факторных признаков x1, x2,…, x k-1.