|
|
ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧЗадача 1.По данным таблицы о распределении проб на обогатительной фабрике по проценту содержания металла в руде (в процентах к итогу) вычислить: 1) среднее содержание металла в руде (обычным способом и по способу моментов); 2) медиану; 3) моду; 4) размах вариации; 5) среднее линейное отклонение; 6) дисперсию (двумя способами); 7) среднее квадратическое отклонение; 8) относительные показатели вариации; 9) асимметрию, эксцесс; Произвести краткий анализ полученных показателей
Решение. 1) определим среднее содержание металла в руде: а) обычным способом:
б) по способу моментов:
где m1- момент первого порядка; К- величина интервала; А- условное начало отсчета.
В качестве условного начала отсчета (т.к. у нас нечетное количество групп) берем центральное значение интервала стоящего в середине, т. е. интервала 20-24 Расчет приведен в таблице 1. К = 12- 8 =4 % А = 22 %
Вывод: Среднее содержание металла в руде составляет 18,76 %.
2) Вычислим медиану. Место медианы - Медианным является интервал 16-20%. т. к. в этом интервале находятся номера 50 и 51 ряда.
Вывод: В половине проб содержание металла в руде больше 18,9 %.
3) Вычислим моду: Модальным в данном распределении является интервал 8-12%, т.к. наибольшее число проб (
Вывод: Больше всего проб с содержание металла равным 10,67 %.
Для расчета показателей вариации удобно использовать вспомогательную таблицу 2.1.
4) Вычислим размах вариации: R = Вывод:Разница между максимальным и минимальным содержанием металла в руде составляет 28% 5) Вычислим среднее линейное отклонение:
6) Вычислим дисперсию: 1 способ:
2 способ:
Вывод: Средний квадрат отклонений индивидуальных значений признаков от их средней величины равен 51,1.
7) Среднее квадратическое отклонение:
Вывод: Индивидуальные значения признака отличаются в среднем от средней арифметической на 7,15%
8) Вычислим относительные показатели вариации: а) коэффициент осцилляции:
б) линейный коэффициент вариации:
в) коэффициент вариации:
Вывод: Значение коэффициента вариации (38,11%) свидетельствует о том, что совокупность не однородна. Таблица 2.1.
9) Вычислим асимметрию и эксцесс:
где
Вывод: Эксцесс отрицателен, следовательно, распределение плосковершинное.
Задача 2.По данным таблицы вычислить: 1) изменение (в %) выпуска каждого вида продукции, а также изменение выпуска продукции в целом по предприятию; 2) изменение цен (в %) по каждому виду продукции и среднее изменение цен по всему ассортименту продукции; 3) агрегатный индекс изменения общей стоимости продукции и провести факторный анализ изменения общей стоимости продукции, выделив из общей суммы изменение за счет изменения количества продукции и за счет изменения цен.
Решение. 1) Для характеристики изменения выпуска каждого вида продукции исчисляются индивидуальные индексы физического объема продукции:
Вывод: Выпуск продукции А вырос на 8 % (108-100).
Вывод: Выпуск продукции Б снизился на 22% (78-100).
Для характеристики изменения выпуска продукции в целом по предприятию исчисляется агрегатный индекс физического объема продукции:
Вывод: Фактический объем производства двух видов продукции снизился на 0,8%, в результате стоимость продукции снизилась на 1500 руб. (195000-196500)
2) Для характеристики изменения цен по каждому виду продукции используются индивидуальные индексы цен:
Вывод: Цена продукции А выросла на 2% (102-100)
Вывод: Цена продукции Б снизилась на 4% (96-100)
Среднее изменение цен по всему ассортименту продукции определяется по формуле агрегатного индекса цен:
Вывод:Фактическая цена по двум видам продукции увеличилась на 0,8% по сравнению с 1 кварталом, за счет чего стоимость продукции повысилась на 1500 руб. (196500-195000)
3) Агрегатный индекс общей стоимости продукции (индекс товарооборота):
Вывод: Общая стоимость обоих товаров не изменилась
Факторный анализ общей стоимости продукции: Общее изменение стоимости продукции:
а) Общее изменение стоимости продукции за счет изменения цены:
б) Общее изменение стоимости продукции за счет изменения количества товара:
Вывод: Изменение цен на оба вида продукции дало прирост общей стоимости продукции в 1500 руб., изменение физического объема продаваемой продукции дало снижение общей стоимости в 1500 руб.
Задача 3.Изобразите графически динамику ряда с помощью статистической кривой. По данным таблицы вычислить: 1) средний объем производства продукции; 2) базисные и цепные абсолютные приросты; 3) базисные и цепные темпы роста; 4) базисные и цепные темпы пророста; 5) абсолютный размер 1% прироста 6) среднегодовой абсолютный прирост; 7) среднегодовой темп роста; 8) произвести аналитическое выравнивание; 9) спрогнозировать объем производства на 5 лет вперед методом экстраполяции; 10) расчетные уровни нанесите на график. Результаты представьте в табличной форме.
Решение. 1) Средний уровень интервального ряда динамики:
2) Расчет показателей динамики представлен в таблице 2.2. Таблица 2.2.
6) Среднегодовой абсолютный прирост:
Вывод: В среднем прирост цен ежегодно составлял 1,5 млн. руб.
7) Среднегодовой темп роста:
Вывод:В среднем цены ежегодно возрастали на 9,2% (109,2-100)
8) Для определения формы тренда и расчета его параметров составляется вспомогательная таблица 2.3. Таблица 2.3.
Первые разности (гр.3) приблизительно равны между собой, что позволяет в виде модели принять уравнение прямой:
Для нахождения
Модель тренда: Теоретические уровни
Далее расчеты приведены в таблице 2.3.
9) Cпрогнозировать объем производства на 5 лет вперед методом экстраполяции:
10)
Задача 4.По данным таблицы необходимо: 1) найти уравнение корреляционной связи между выпуском продукции, размером основных фондов и численностью рабочих; 2) определить выровненные значения Y(X) и построить график корреляционной зависимости по фактическим и теоретическим данным; 3) определить коэффициенты парной и множественной корреляции. Численность выразить в тыс. чел.
Решение. Таблица 2.4.
1) Уравнение множественной корреляции:
где х – стоимость ОПФ, млн. руб.; z – численность рабочих, тыс. чел.; y – выпуск продукции, млн. руб.; n - количество предприятий. Для нахождения неизвестных параметров
В уравнение подставляем данные х, z, y из таблицы.
Получаем уравнение множественной корреляции:
Вывод: Уравнение показывает влияние двух признаков-факторов х (стоимость ОПФ) и z (численность рабочих) на результативный признак y (выпуск продукции). Параметры уравнения
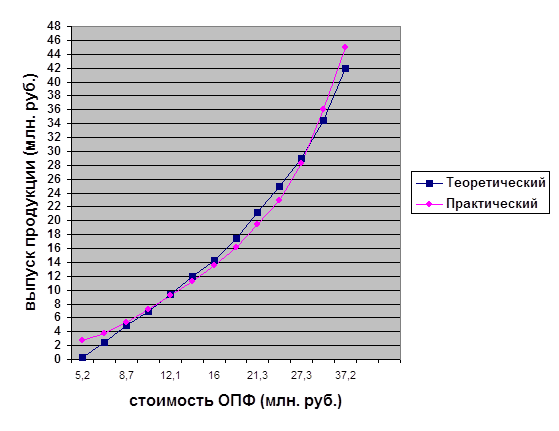
2) Определим выровненные значения у(х) и построим график корреляционной зависимости по фактическим и теоретическим данным Используем уравнение прямолинейной функции: у(х) =
у(х) = -6,46+1,3х - уравнение парной корреляции между выпуском продукции и стоимостью ОПФ. Строим график корреляционной зависимости по фактическим и теоретическим данным:
3) Коэффициент парной корреляции между стоимостью ОПФ и выпуском продукции:
Вывод: Связь между стоимостью ОПФ и выпуском продукции прямая, слабая.
Коэффициент парной корреляции между численностью рабочих и выпуском продукции:
Вывод:Связь прямая, сильная.
Коэффициент парной корреляции между численностью рабочих и стоимостью ОПФ:
Вывод: Связь прямая, сильная.
Коэффициент множественной корреляции:
Вывод: Между стоимостью ОПФ, численностью рабочих и выпуском продукции существует сильная связь. За счет вариации х, у, z объясняется 98,7% общей вариации дохода производства.
Задача 5.Произведена простая случайная повторная выборка 100 рабочих механического цеха по общему стажу работы (см. таблицу). Определить: 1) средний стаж рабочих цеха с вероятностью 0,683; 2) долю рабочих со стажем 20 лет и более с вероятностью 0,997; 3) необходимую численность выборки при определении среднего стажа работы с вероятностью 0,954, чтобы предельная ошибка выборки не превышала 2 г.
Решение.
1) Средний стаж рабочих цеха с вероятностью 0,683:
Найдем выборочную среднюю:
Найдем предельную ошибку выборки:
Вывод:с вероятностью 0,683 можно говорить, что средний стаж работы персонала цеха колеблется от 16,31 до 17,79 лет.
2) Определим долю рабочих со стажем работы 20 лет и более с вероятностью 0,997
Таким образом, доля рабочих со стажем 20 лет и более составляет 20%.
Вывод:с вероятностью 0,997 можно говорить, что доля рабочих предприятия со стажем работы 20 лет и более колеблется от 8% до 32%.
3) Предельная ошибка выборки
Вывод:с вероятностью 0,954 численность выборки составляет 62 человека, при этом предельная ошибка выборки не превышает 2 лет.
Задача 6.По данным о продукции, основных фондах и среднесписочной численности рабочих предприятий объединения (табл. задачи 4): 1) произвести группировку предприятий (с равными интервалами по стоимости основных производственных фондов); 2) группы охарактеризовать числом предприятий, а также объемом выпуска продукции, численностью рабочих, размерами основных фондов; 3) вычислить по группам средние показатели: на одно предприятие - размер основных фондов, фондоотдачи, фондоемкости, объем выпуска продукции, численность рабочих, производительность труда, фондовооруженность. 4) результаты группировки изложить в табличной форме и сформулировать краткие выводы.
Решение. Существенный признак – стоимость ОПФ. 1) Найдем количество групп:
Рассчитаем величину интервала: i = (37,2 – 5,2) / 6 = 5,33 млн. руб. Произведем группировку (результаты группировки представлены в таблице 2.5.).
3) Рассчитаем фондоотдачу, фондоемкость, фондовооруженность и производительность труда. а) Фондоотдача – характеризует количество продукции, приходящейся на 1 руб. стоимости основных фондов. Фо = где Q – объем производства продукции;
б) Фондоемкость – показывает какая, часть стоимости основных фондов приходится на 1 руб. произведенной продукции. Фе = Фе1 = в) Производительность труда – это количество продукции приходящееся на одного среднесписочного работника. П = где П1 = г) Фондовооруженность труда – это размер основных фондов в расчете на одного работника предприятия. Фт = Фт1 = Вывод:С ростом стоимости основных производственных фондов увеличиваются выпуск продукции на 1 предприятие, фондоотдача, возрастает фондовооруженность труда, а фондоемкость уменьшается.
Таблица 2.5.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ Задача 1 По данным таблицы о распределении рабочих по стажу работы на металлургическом заводе вычислить: 1) средний стаж работы (обычным способом и по способу моментов); 2) медиану; 3) моду; 4) размах вариации; 5) среднее линейное отклонение; 6) дисперсию (двумя способами); 7) среднее квадратическое отклонение; 8) относительные показатели вариации; 9) асимметрию, эксцесс; Произвести краткий анализ полученных показателей.
Задача 2 По данным таблицы вычислить: 1) изменение (в %) выпуска каждого вида продукции, а также изменение выпуска продукции в целом по предприятию; 2) изменение цен (в %) по каждому виду продукции и среднее изменение цен по всему ассортименту продукции; 3) агрегатный индекс изменения общей стоимости продукции и провести факторный анализ изменения общей стоимости продукции, выделив из общей суммы изменение за счет изменения количества продукции и за счет изменения цен. |
|
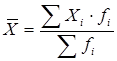
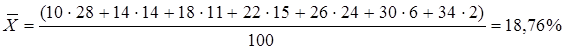
 - среднеарифметическая,
- среднеарифметическая,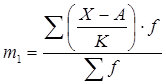

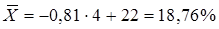
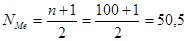
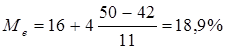
 =28) находится в этом интервале.
=28) находится в этом интервале.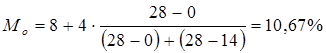
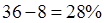
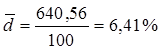
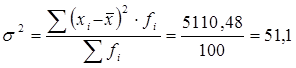
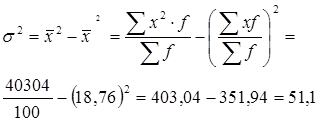
 %
%
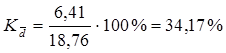
 -
-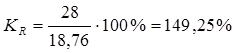
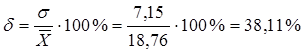








 ,
,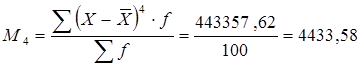
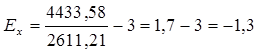
 )
)
 )
)
 )
)
 )
)
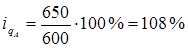
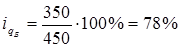
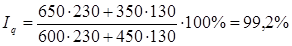


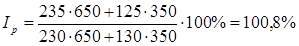

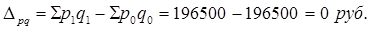
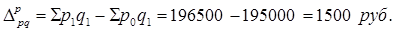
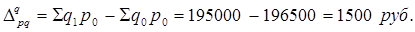
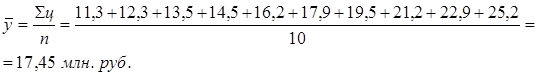
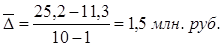
 или 109,2%
или 109,2%

 и
и  используется система нормальных уравнений. Для упрощения системы уравнений показатели времени t обозначаются так, чтобы
используется система нормальных уравнений. Для упрощения системы уравнений показатели времени t обозначаются так, чтобы  ; тогда система принимает вид:
; тогда система принимает вид: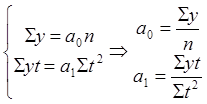
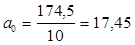
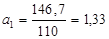
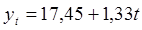
 млн. руб.
млн. руб.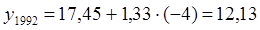 млн. руб.
млн. руб.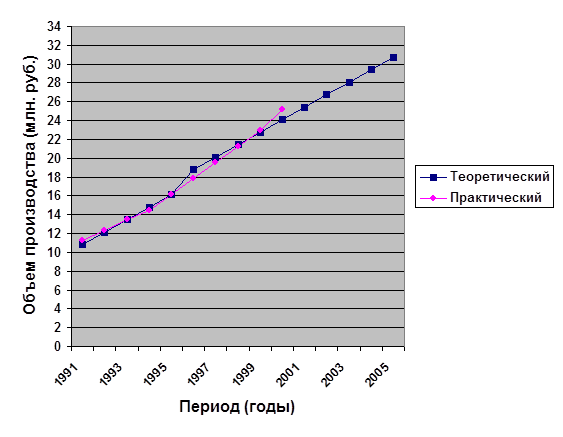





 ,
, составляем систему нормальных уравнений:
составляем систему нормальных уравнений:


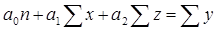
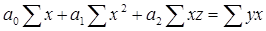
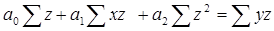
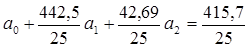
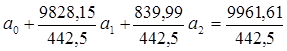

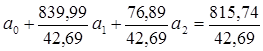
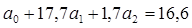
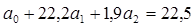
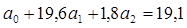
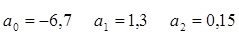
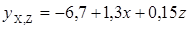
 и
и  показывают, что с увеличением стоимости ОПФ на 1млн. руб. и численности персонала на 1000 человек выпуск продукции возрастает соответственно на 1,3 и 0,15 млн. руб.
показывают, что с увеличением стоимости ОПФ на 1млн. руб. и численности персонала на 1000 человек выпуск продукции возрастает соответственно на 1,3 и 0,15 млн. руб.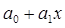
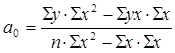
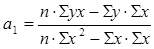
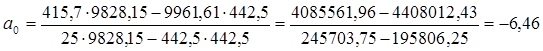
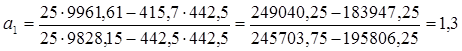
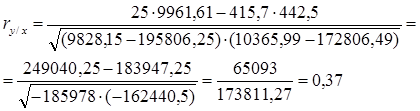
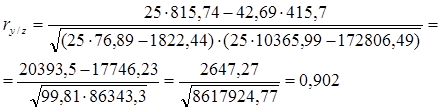
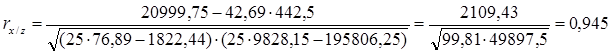

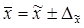

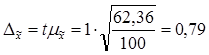

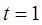
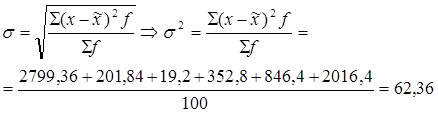
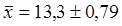
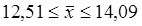
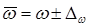
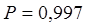

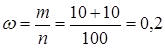
 или 12 %
или 12 %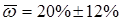
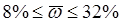
 = 2 года
= 2 года 
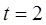
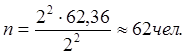
 групп
групп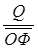
 - среднегодовая стоимость основных производственных фондов. Фо1 =
- среднегодовая стоимость основных производственных фондов. Фо1 =  млн. руб. (далее смотри таблицу)
млн. руб. (далее смотри таблицу)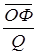
 млн. руб.
млн. руб.
 - среднесписочная численность работников за период.
- среднесписочная численность работников за период. млн. руб./чел.
млн. руб./чел.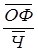
 млн.руб./чел.
млн.руб./чел.