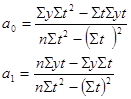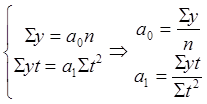|
|
Формулы для определения численности простой случайной выборки
Ряды динамики
Ряд динамики — это последовательность упорядоченных во времени числовых показателей, характеризующих уровень развития изучаемого явления. Всякий ряд динамики включает, следовательно, два обязательных элемента, во-первых, время и, во-вторых, конкретное значение показателя, или уровень ряда. Различают моментные и интервальные ряды динамики. Интервальный ряд динамики — последовательность, в которой уровень явления относится к результату, накопленному или вновь произведенному за определенный интервал времени. Если же уровень ряда показывает фактическое наличие изучаемого явления в конкретный момент времени, то совокупность уровней образует моментный ряд динамики. При изучении явления во времени перед исследователем встает проблема описания интенсивности изменения и расчета средних показателей динамики. Решается она путем построения соответствующих показателей. Для характеристики интенсивности изменения во времени такими показателями будут: 1) абсолютный прирост, 2) темпы роста, 3) темпы прироста, 4) абсолютное значение одного процента прироста. В случае, когда сравнение проводится с периодом (моментом) времени, начальным в ряду динамики, получают базисные показатели. Если же сравнение производится с предыдущим периодом или моментом времени, то говорят о цепных показателях. Расчет показателей динамики представлен в таблице: Таблица 1.4.
При расчете показателей приняты следующие условные обозначения: уi – уровень любого периода (кроме первого), называемый текущим; уi-1 – уровень периода, предшествующего текущему; у0 – уровень, принятый за базу сравнения (часто начальный уровень).
Система средних показателей динамики включает: средний уровень ряда, средний абсолютный прирост, средний темп роста, средний темп прироста. Средний уровень ряда — это показатель, обобщающий итоги развития явления за единичный интервал или момент из имеющейся временной последовательности. Расчет среднего уровня ряда динамики определяется видом этого ряда и величиной интервала, соответствующего каждому уровню. 1. Для интервальных рядов с равными периодами времени средний уровень ряда рассчитывается следующим образом;
где n — число уровней ряда. 2. Если в интервальном ряду отрезки имеют неравную длительность, то средний уровень рассчитывается по формуле средней арифметической:
где t – продолжительность периода, в течение которого уровень не менялся. 3. Для моментного ряда с равноотстоящими моментами используется формула средней хронологической.
Средний абсолютный прирост рассчитывается по формулам в зависимости от способа нумерации интервалов (моментов).
Средний темп роста:
где К — коэффициент роста. Средний темп прироста(%) определяется по единственной методологии:
Средняя величина абсолютного значения 1% прироста:
Всякий ряд динамики теоретически может быть представлен в виде составляющих: 1) тренд — основная тенденция развития динамического ряда (к увеличению либо снижению его уровней); 2) циклические (периодические) колебания, в том числе сезонные; 3) случайные колебания. Выделение тренда может быть произведено тремя методами. 1. Укрупнение интервалов. Ряд динамики разделяют на некоторое достаточно большое число равных интервалов. Если средние уровни по интервалам не позволяют увидеть тенденцию развития явления, переходят к расчету уровней за большие промежутки времени, увеличивая длину каждого интервала (одновременно уменьшается количество интервалов). 2. Скользящая средняя. В этом методе исходные уровни ряда заменяются средними величинами, которые получают из данного уровня и нескольких симметрично его окружающих. Целое число уровней, по которым рассчитывается среднее значение, называют интервалом сглаживания. Интервал может быть нечетным (3, 5, 7 и т. д. точек) или четным (2, 4, 6 и т.д. точек). При нечетном сглаживании полученное среднее арифметическое значение закрепляют за серединой расчетного интервала, при четном этого делать нельзя. Поэтому при обработке ряда четными интервалами их искусственно делают нечетными, для чего образуют ближайший больший нечетный интервал, но из крайних его уровней берут только 50 %. Формулы расчета скользящей средней выглядят, в частности, следующим образом: для 3-х членной: Полученные средние записываются к соответствующему срединному интервалу (второму, третьему, четвертому и т. д.). Если период скользящей четный, то выполняют центрирование данных, т. е. определение средней из найденных средних, что необходимо для определения срединного периода. Например, если исчисляется скользящая с продолжительностью периода, равной 2, то расчет производится следующим образом:
Тогда центрированные средние равны:
Первая центрированная средняя будет отнесена ко второму периоду, вторая - к третьему и т. д. Сглаженный ряд «укорачивается» по сравнению с фактическим на 3. Аналитическое выравнивание. Под этим понимают определение основной проявляющейся во времени тенденции развития изучаемого явления. Развитие предстает перед исследователем как бы в зависимости только от течения времени. В итоге выравнивания временного ряда получают наиболее общий, суммарный, проявляющийся во времени результат действия всех причинных факторов. Отклонение конкретных уровней ряда от уровней, соответствующих общей тенденции, объясняют действием факторов, проявляющихся случайно или циклически. В результате приходят к трендовой модели:
Вид уравнения определяется характером динамики развития конкретного явления. Логический анализ при выборе вида уравнения может быть основан на рассчитанных показателях динамики, а именно: • если относительно стабильны абсолютные приросты (первые разности уровней приблизительно равны), сглаживание может быть выполнено по прямой; • если абсолютные приросты равномерно увеличиваются (вторые разности уровней приблизительно равны), можно принять параболу второго порядка; • при ускоренно возрастающих (замедляющихся) абсолютных приростах - параболу третьего порядка; • при относительно стабильных темпах роста - показательную функцию. На практике выбор формы кривой может быть основан на анализе графического изображения уровней динамического ряда (линейной диаграммы); при этом целесообразнее воспользоваться графическим изображением сглаженных уровней, в которых случайные колебания погашены. Если условия формирования уровней ряда изменяются, то расчет параметров уравнения не следует вести по данным за весь рассматриваемый период. В этом случае было бы целесообразно разбить ряд динамики на ряд периодов, основываясь на оценке устойчивости показателей динамики. Чаще всего при выравнивании используются линейная зависимость.
Для нахождения параметров прямой используют систему уравнений: na0 + a1St = Sy a0St + a1St2 = Syt Решение системы относительно искомых параметров а0 и а1:
Упрощенный расчет параметров уравнения заключается в переносе начала координат в середину ряда динамики. В этом случае упрощаются сами нормальные уравнения, кроме того, уменьшаются абсолютные значения величин, участвующих в расчете. В самом деле, если до переноса начала координат t было равно 1, 2, 3, …, n, то после переноса t = … -4, -3, -2, -1, 0, 1, 2, …, если число членов ряда нечетное. Когда же число ряда четное, то t = …, -3, -2, -1, 1, 2, 3,… При таких условиях системы нормальных уравнений для прямой упрощаются:
Индексы Индексы относятся к важнейшим обобщающим показателям. В статистике под индексом понимается относительный показатель, характеризующий изменение уровней сложных социально-экономических показателей во времени, в пространстве или сравнение фактических данных с любым эталоном (план, прогноз, норматив и т. д.). Сложный показатель состоит из непосредственно несоизмеримых (несуммируемых) элементов. Индекс является результатом сравнения двух одноименных показателей, поэтому при их вычислении различают сравнимый уровень (числитель индексного отношения), называемый текущим или отчетным, и уровень, с которым производится сравнение (знаменатель индексного отношения), называемый базисным. Выбор базы определяется целью исследования. Все экономические индексы можно классифицировать по следующим признакам: По степени охвата явления индексы бывают индивидуальные и сводные. ü Индивидуальные индексы служат для характеристики изменения отдельных элементов сложного явления. ü Для измерения динамики сложного явления, составные части которого непосредственно несоизмеримы (изменения физического объема продукции, включающей разноименные товары, индекса цен акций предприятий региона и т. п.), рассчитываютсводные, илиобщие индексы. В зависимости от формы построения: ü агрегатные.Эта форма общих индексов является основной формой экономических индексов. ü средние: арифметические и гармонические. Средние индексы - производные, они получаются в результате преобразования агрегатных индексов. По характеру объема исследования общие индексы подразделяются на индексы количественных (объемных) и качественных показателей. В основе такого деления индексов лежит вид индексируемой величины. По объекту исследования индексы бывают: производительности труда, себестоимости, физического объема продукции, стоимости продукции и т. д. По составу явления: ü постоянного (фиксированного) состава; ü переменного состава. В международной практике индексы принято обозначать символами i и I (начальная буква латинского слова index). Буквой «i» обозначаются индивидуальные (частные) индексы, буквой «I» - общие индексы. Знак внизу справа означает период: 0-базисный; 1-отчетный. Помимо этого используются определенные символы для обозначения индексируемых показателей: q - количество (объем) какого-либо товара в натуральном выражении; р — цена единицы товара; z - себестоимость единицы продукции; t - затраты времени на производство единицы продукции; w - выработка продукции в стоимостном выражении на одного рабочего или в единицу времени; v - выработка продукции в натуральном выражении на одного рабочего или в единицу времени; Т - общие затраты времени (tq) или численность рабочих; pq - стоимость продукции или товарооборот; zq - издержки производства. |
|




 )
)




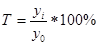





 ,
, ,
, .
. или
или 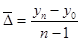
 или
или 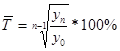
 .
. .
. ;
;  ;
; 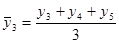 и т.д.
и т.д. ;
;  ;
;  и т.д.
и т.д. ;
;  и т.д.
и т.д. члена с одного и другого конца, где т – количество уровней, входящих в интервал.
члена с одного и другого конца, где т – количество уровней, входящих в интервал. .
.