Связь угловых и линейных величин. Скорость.
Скорость- векторная физическая величина, служащая для характеристики направления и быстроты движения точки в механике. Средней скоростью точки в промежутке времени от 
до  называется вектор называется вектор  , равный отношению приращения , равный отношению приращения  радиуса-вектора точки за этот промежуток времени к его продолжительности радиуса-вектора точки за этот промежуток времени к его продолжительности  : :
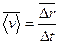
Средняя скорость направлена так же, как вектор перемещения  , то есть вдоль хорды, стягивающей соответствующий участок траектории точки. , то есть вдоль хорды, стягивающей соответствующий участок траектории точки.
Скоростью точки в момент времени  называется вектор называется вектор  , равный первой производной по времени от радиуса-вектора этой точки: , равный первой производной по времени от радиуса-вектора этой точки:

 . .
Вектор  можно разложить по базису можно разложить по базису  , то есть на три составляющие по осям прямоугольной декартовой системы координат. , то есть на три составляющие по осям прямоугольной декартовой системы координат.

 . .
 . .
Если направление вектора  скорости точки не изменяется, то траектория точки- прямая линия. При равномерном движении точки остается постоянным модуль ее скорости скорости точки не изменяется, то траектория точки- прямая линия. При равномерном движении точки остается постоянным модуль ее скорости  , а путь, пройденный точкой за промежуток времени от , а путь, пройденный точкой за промежуток времени от  до до  , ,  . .
Радиус кривизны траектории.
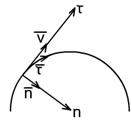





 . .
Ускорение.
Ускорение- векторная физическая величина, характеризующая быстроту изменения скорости  . .
Ускорением называется вектор  , равный первой производной по времени , равный первой производной по времени  от скорости от скорости  этой точки. Ускорение точки также равно второй производной по времени от радиуса-вектора этой точки. Ускорение точки также равно второй производной по времени от радиуса-вектора  этой точки: этой точки:
 . .
Разложение ускорения точки по базису  , то есть на составляющие по осям прямоугольной декартовой системы координат, имеет вид: , то есть на составляющие по осям прямоугольной декартовой системы координат, имеет вид:
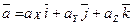 , где , где
 , ,  , ,  . .
Здесь  , ,  , ,  - компоненты скорости точки, а - компоненты скорости точки, а  - координаты точки в рассматриваемый момент времени. - координаты точки в рассматриваемый момент времени.
Если траектория точки- плоская кривая, то ускорение  точки лежит в этой плоскости. В общем случае траектория точки- пространственная кривая, а ускорение точки лежит в этой плоскости. В общем случае траектория точки- пространственная кривая, а ускорение  лежит в соприкасающейся плоскости. В соприкасающейся плоскости есть два избранных направления- касательной к траектории (орт лежит в соприкасающейся плоскости. В соприкасающейся плоскости есть два избранных направления- касательной к траектории (орт 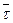 ) и главной нормали (орт ) и главной нормали (орт  ). Поэтому вектор ). Поэтому вектор  удобно разложить на две составляющие вдоль этих направлений, то есть по базису удобно разложить на две составляющие вдоль этих направлений, то есть по базису 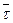 , n: , n:

Составляющая  называется касательным или тангенциальным ускорением точки, а составляющая называется касательным или тангенциальным ускорением точки, а составляющая  - нормальным ускорением точки. - нормальным ускорением точки.
Для нахождения значений  и и  компонент вектора компонент вектора  воспользуемся выражением для скорости точки воспользуемся выражением для скорости точки  . Следовательно, . Следовательно,
 . .

 . .
 При перемещении по траектории на малое расстояние При перемещении по траектории на малое расстояние  единичный вектор касательной поворачивается на угол единичный вектор касательной поворачивается на угол  . Из равнобедренного треугольника векторов видно, что ввиду малости . Из равнобедренного треугольника векторов видно, что ввиду малости  , а по направлению вектор , а по направлению вектор 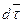 совпадает с ортом главной нормали совпадает с ортом главной нормали  . Таким образом: . Таким образом:

  . .
Равнопеременное движение материальной точки.
Движение точки называется равнопеременным, если в этом движении  , то есть за равные промежутки времени модуль скорости точки изменяется на одинаковые величины. , то есть за равные промежутки времени модуль скорости точки изменяется на одинаковые величины.
 и и  . .  , ,  , ,  . .
 . .
Так как  =const, то =const, то 
Так как  , то зависимость от времени координаты , то зависимость от времени координаты  какой-либо точки тела имеет вид: какой-либо точки тела имеет вид:
 , где , где  и и  значения значения  и и  в момент начала отсчета времени (t=0). в момент начала отсчета времени (t=0).
БИЛЕТ 2. Движение материальной точки по окружности. Связь угловых и линейных величин.
Движение твердого тела, при котором все точки прямой АВ, жестко связанной с телом остаются неподвижными, называется вращением тела вокруг неподвижной оси. Прямая AB называется осью вращения тела.
Для описания вращательного движения тела неудобно пользоваться такими понятиями кинематики точки, как перемещение, пройденный путь, скорость и ускорение точки. В этом случае мерой перемещения всего тела за малый промежуток времени  служит вектор служит вектор  элементарного поворота тела. По модулю он равен углу элементарного поворота тела. По модулю он равен углу 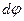 поворота тела вокруг оси за время поворота тела вокруг оси за время  и направлен вдоль оси вращения по правилу правого винта: из конца вектора и направлен вдоль оси вращения по правилу правого винта: из конца вектора  поворот тела виден происходящим против хода часовой стрелки. поворот тела виден происходящим против хода часовой стрелки.

Кинематической характеристикой направления и быстроты вращения служит угловая скорость тела,равная отношению вектора элементарного поворота тела к продолжительности этого поворота:

 , ,  , ,  , ,  . .
 . .
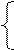 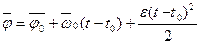 . .
 . .
Связь угловых и линейных величин.
1). 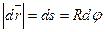
2). 

Пусть материальная точка движется по окружности радиуса R. Тогда
 . Разделим левую и правую части уравнения на . Разделим левую и правую части уравнения на 
    . Векторы . Векторы   взаимно перпендикулярны. Сместим все векторы в одну точку (точка А). взаимно перпендикулярны. Сместим все векторы в одну точку (точка А).
 , , 
 , ,  . .
БИЛЕТ 3. Поступательное, вращательное и сложное движение твердого тела. Связь скоростей различных точек твердого тела при сложном движении.
Поступательное:

 Вращательное: Вращательное:

Сложное:
|

 называется вектор
называется вектор  , равный отношению приращения
, равный отношению приращения  радиуса-вектора точки за этот промежуток времени к его продолжительности
радиуса-вектора точки за этот промежуток времени к его продолжительности  :
: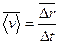
 , равный первой производной по времени от радиуса-вектора этой точки:
, равный первой производной по времени от радиуса-вектора этой точки:
 .
. , то есть на три составляющие по осям прямоугольной декартовой системы координат.
, то есть на три составляющие по осям прямоугольной декартовой системы координат.
 .
. .
. .
.





 .
. , равный первой производной по времени
, равный первой производной по времени  этой точки:
этой точки: .
.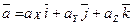 , где
, где ,
,  ,
,  .
. ,
,  ,
,  - компоненты скорости точки, а
- компоненты скорости точки, а  - координаты точки в рассматриваемый момент времени.
- координаты точки в рассматриваемый момент времени.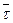 ) и главной нормали (орт
) и главной нормали (орт  ). Поэтому вектор
). Поэтому вектор 
 называется касательным или тангенциальным ускорением точки, а составляющая
называется касательным или тангенциальным ускорением точки, а составляющая  - нормальным ускорением точки.
- нормальным ускорением точки. и
и  компонент вектора
компонент вектора  . Следовательно,
. Следовательно, .
.
 .
. При перемещении по траектории на малое расстояние
При перемещении по траектории на малое расстояние  единичный вектор касательной поворачивается на угол
единичный вектор касательной поворачивается на угол  . Из равнобедренного треугольника векторов видно, что ввиду малости
. Из равнобедренного треугольника векторов видно, что ввиду малости  , а по направлению вектор
, а по направлению вектор 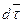 совпадает с ортом главной нормали
совпадает с ортом главной нормали 

 .
. , то есть за равные промежутки времени модуль скорости точки изменяется на одинаковые величины.
, то есть за равные промежутки времени модуль скорости точки изменяется на одинаковые величины. и
и  .
.  ,
,  ,
,  .
. .
.
 , то зависимость от времени координаты
, то зависимость от времени координаты  какой-либо точки тела имеет вид:
какой-либо точки тела имеет вид: , где
, где  и
и  значения
значения  в момент начала отсчета времени (t=0).
в момент начала отсчета времени (t=0). служит вектор
служит вектор  элементарного поворота тела. По модулю он равен углу
элементарного поворота тела. По модулю он равен углу 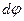 поворота тела вокруг оси за время
поворота тела вокруг оси за время 

 ,
,  ,
,  .
. .
.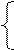
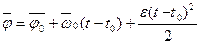 .
. .
.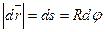


 . Разделим левую и правую части уравнения на
. Разделим левую и правую части уравнения на 


 . Векторы
. Векторы 
 взаимно перпендикулярны. Сместим все векторы в одну точку (точка А).
взаимно перпендикулярны. Сместим все векторы в одну точку (точка А). ,
, 
 ,
,  .
.
 Вращательное:
Вращательное: