|
|
Потенциальная энергия тела в положении равновесия.
БИЛЕТ 9. Потенциальная энергия материальной точки в поле силы тяжести, в поле центральной силы. Потенциальная энергия системы из двух взаимодействующих материальных точек. - в поле силы тяжести.
(
- в поле центральной силы. Поле называется центральным, если сила, действующая на материальную точку, помещенную в это поле, направлена вдоль прямой, соединяющей ее с ее центром.
БИЛЕТ 10. Закон изменения механической энергии. Закон сохранения механической энергии. Абсолютно упругий удар.
Рассмотрим произвольную механическую систему, состоящую из n материальных точек. Ее кинетическая энергия
причем сумму элементарных работ
Тогда
Из определения потенциальной энергии системы
Величина W, равная сумме кинетической и потенциальной энергий системы, называется механической энергией (полной механической энергией) системы. Уравнение выражает закон изменения механической энергии:
изменение механической энергии системы равно алгебраической сумме работ всех непотенциальных сил, действующих на систему, и изменения потенциальной энергии системы за рассматриваемый промежуток времени, обусловленного нестационарностью внешних потенциальных сил.
Если система замкнута, то изменение ее механической энергии обусловлено только действием в ней непотенциальных сил:
Механическая система называется консервативной,если все действующие на нее внешние и внутренние непотенциальные силы не совершают работы ( Поэтому видно, что механическая энергия консервативной системы не изменяется с течением времени. Этот закон называется законом сохранения механической энергии.В частности, он справедлив для замкнутых консервативных систем: механическая энергия замкнутой системы не изменяется, если все внутренние силы потенциальны либо не совершают работы. Например, силы трения покоя и гироскопические силы работы не совершают. Поэтому действие таких сил на систему не вызывает изменения ее механической энергии.
Применение закона сохранения механической энергии к расчету абсолютно упругого прямого центрального удара двух тел.
Абсолютно упругим ударомназывается такой удар, при котором механическая энергия соударяющихся тел не преобразуется в другие виды энергии.
В процессе удара систему соударяющихся упругих тел можно считать замкнутой и консервативной. Следовательно, для решения этой задачи можно воспользоваться законами сохранения механической энергии и импульса. Перед ударом и после его завершения соударяющиеся тела не деформированы, так что потенциальную энергию системы в этих двух состояниях можно считать одинаковой и равной нулю. Тогда из закона сохранения механической энергии имеем
По закону сохранения импульса:
Так как все скорости направлены по оси ОХ, то
(проекции векторов скоростей на ось ОХ)
Совместное решение уравнений дает
Окончательно получаем:
БИЛЕТ 11. Теорема Кёнига.
Значения скорости и кинетической энергии одной и той же материальной точки различны в двух системах отсчета, движущихся друг относительно друга. Рассмотрим 2 системы отсчета: инерциальную систему и систему, движущуюся относительно первой системы со скоростью
Формулировка:
«Кинетическая энергия механической системы равна сумме кинетической энергии той же системы в ее движении относительно системы центра масс и кинетической энергии, которую имела бы рассматриваемая система, двигаясь поступательно со скоростью центра масс»
БИЛЕТ 12. Момент силы относительно неподвижной точки и оси. Момент пары сил. Момент импульса материальной точки и системы материальных точек относительно неподвижной точки и оси. Момент силы - относительно неподвижной точки Моментом силы
Точка
(где
- относительно неподвижной оси. Моментом силы относительно неподвижной оси а называется скалярная величина Также
0 (направлено вдоль оси oo’)
Момент пары сил.
Момент пары сил не зависит от выбора оси
Момент импульса: - материальной точки относительно неподвижной точки
- системы материальных точек относительно неподвижной точки Моментом импульса механической системы относительно неподвижной точки
- материальной точки относительно неподвижной оси.
- системы материальных точек относительно неподвижной оси. Моментом импульса механической системы относительно оси называется проекция на эту ось вектора момента импульса системы относительно любой точки, выбранной на рассматриваемой оси.
БИЛЕТ 13. Момент инерции относительно оси. Теорема Штейнера. Примеры расчета момента инерции. Величина
Момент инерции: Материальной точки Системы материальных точек Абсолютно твердого тела
Таким образом, момент импульса тела относительно оси ОZ равен
Теорема Штейнера: Момент инерции
проходящей через центр масс
На рисунке оси
где
так как центр масс совпадает с началом координат
|
|
 (
(  ).
). (
(  ).
). (
(  ).
).
 (
(  ).
).











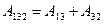
 ) =
) =  =
=  =
=  .
.




 =0, так как
=0, так как  ,
, 





 =
= 




 Потенциальная энергия системы из двух взаимодействующих материальных точек.
Потенциальная энергия системы из двух взаимодействующих материальных точек.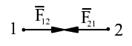
 =
= 




 ).
).
 , а изменение кинетической энергии равно сумме работ, совершаемых при этом всеми внешними и внутренними силами:
, а изменение кинетической энергии равно сумме работ, совершаемых при этом всеми внешними и внутренними силами: ,
, всех сил, приложенных к
всех сил, приложенных к  материальной точке системы удобно разбить на две части:
материальной точке системы удобно разбить на две части: .
.

 следует, что согласно
следует, что согласно




 Анпс = 0), а все внешние потенциальные силы стационарны. Потенциальная энергия консервативной системы может изменяться только при изменении конфигурации системы. Следовательно, частная производная по времени от потенциальной энергии консервативной системы, характеризующая быстроту изменения этой энергии с течением времени при условии постоянства конфигурации системы, тождественно равна нулю:
Анпс = 0), а все внешние потенциальные силы стационарны. Потенциальная энергия консервативной системы может изменяться только при изменении конфигурации системы. Следовательно, частная производная по времени от потенциальной энергии консервативной системы, характеризующая быстроту изменения этой энергии с течением времени при условии постоянства конфигурации системы, тождественно равна нулю:  .
.  Пусть два абсолютно упругих шара массами
Пусть два абсолютно упругих шара массами 
 и
и  движутся до удара поступательно со скоростями
движутся до удара поступательно со скоростями 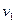 и
и  , направленными вдоль оси ОХ, проходящей через центры шаров. Нужно найти скорости
, направленными вдоль оси ОХ, проходящей через центры шаров. Нужно найти скорости  и
и  шаров после соударения.
шаров после соударения.






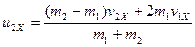
 :
:


 и
и 








 - Теорема Кёнига.
- Теорема Кёнига.
 относительно неподвижной точки
относительно неподвижной точки  называется векторное произведение радиуса-вектора
называется векторное произведение радиуса-вектора  , проведенного из точки
, проведенного из точки  , приложения силы на саму силу.
, приложения силы на саму силу.
 Вектор
Вектор  направлен перпендикулярно плоскости векторов
направлен перпендикулярно плоскости векторов 
 - угол между
- угол между  -длина перпендикуляра, опущенного из точки
-длина перпендикуляра, опущенного из точки 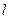 называется плечом силы
называется плечом силы  равная проекции на эту ось вектора момента силы относительно какой-нибудь точки, лежащей на оси а или векторная величина
равная проекции на эту ось вектора момента силы относительно какой-нибудь точки, лежащей на оси а или векторная величина  , где
, где  - орт оси а.
- орт оси а. , (где
, (где  - расстояние от точки приложения силы до оси, а
- расстояние от точки приложения силы до оси, а  - проекция силы F на направление вектора
- проекция силы F на направление вектора  =v/
=v/  , где v-линейная скорость этой точки вращающегося тела.
, где v-линейная скорость этой точки вращающегося тела.






 ] =
] =
 +
+  +
+  +
+ 

 Парой называются силы равные по величине, противоположные по направлению, но не действующие по одной прямой.
Парой называются силы равные по величине, противоположные по направлению, но не действующие по одной прямой.

 (
(  Моментом импульса
Моментом импульса  материальной точки относительно неподвижной точки
материальной точки относительно неподвижной точки  материальной точки, проведенного из точки O, на импульс этой материальной точки
материальной точки, проведенного из точки O, на импульс этой материальной точки 

 равный геометрической сумме моментов импульса относительно той же точки всех материальных точек системы.
равный геометрической сумме моментов импульса относительно той же точки всех материальных точек системы.




 , равная сумме произведений масс
, равная сумме произведений масс  всех материальных точек , образующих механическую систему, на квадраты их расстояний
всех материальных точек , образующих механическую систему, на квадраты их расстояний 










 тела относительно произвольной оси
тела относительно произвольной оси  равен сумме моментов инерции
равен сумме моментов инерции  тела относительно параллельной ей оси
тела относительно параллельной ей оси  ,
, тела и произведения массы тела
тела и произведения массы тела  на квадрат расстояния
на квадрат расстояния  между этими осями.
между этими осями. 
 Доказательство:
Доказательство: до этих осей обозначены соответственно
до этих осей обозначены соответственно  . По теореме косинусов:
. По теореме косинусов:

 - абсцисса элемента
- абсцисса элемента 
 . Справедливость соотношения доказана.
. Справедливость соотношения доказана.