|
|
Геометрический смысл итегральной суммы Римана.Гл.5 Определенный интеграл Рассмотрим одну из множества практических задач, приводящих к определённого интеграла. А именно: задачу о вычислении площади плоских фигур. Пусть дана
Фигура ограничена сверху кривой, при этом Такую фигуру принято называть криволиненейной трапецией. Определим ее площадь. Для этого: 1) разделим (отрезок
Через эти точки проводим прямые || по оси OY. Трапеция разобьется на «n»-полосок Обозначим Для всех полосок имеем: 2) 3) На каждом из промежутков
Размеченное разбиение - Неразмечене разбиение - 4) Найдем значение функции
Заменим каждую полоску прямоугольником с основанием Т.о. площадь криволиненейной трапеции приближенно замениться площадью некоторой ступенчатой фигуры составленой из отдельных прямоугольников
При этом,если уменьшать расстояние между точками
К суммам типа (1) можно прийти решая различные задачи: 1)вычисление длины пути,пройденного точкой за время с момента При заданной скорости движения 2) Определение массы прямоугольного стержня конечной длинны с заданной линейной массовой плотностью и тд. Такие суммы называются интегральными . Df1.Сумма произвдений длин ячеек Т.е Для данной функции Для данной функции Дадим актуальное Df-е Df.2.Пусть дан Упорядоченный набор точек {
Называется разбиением отрезка Обозначение: Очевидно,что различные разбиения олучаем даже в том случае, когда совпадает число точек разбиения. Обозначим
Шагом (мелкостью) разбиения Df.3.Пунктированным разбиением отрезка
Обозначение Очевидно, из одного разбиения Анологично шаг пунктированого разбиения
Пусть теперь дана функция Составим следующую сумму (2) Очевидно Такие функции ранее не рассмотривались. Дадим
Заметим, что для такого вида функций В том числе необходимое условие
J= При этом а называется нижним пределом , b-верхним пределом, Интегралом Римана J=
Df.4’. Если то этот предел называется определенным интегралом функции I=
E-
Что при
Множество ( или класс) функций определеных на [a,b] и интегрируемых на [a,b] обозначается
Геометрический смысл итегральной суммы Римана. Если Это сумма площадей прямоугольников, апроксимирующих ( приближенное выражение математических велечин (чисел,функций) через другие более простые) криволинейную трапецию. По этому интеграл Римана
В этом и заключаеться геометрический смысл определенного интеграла.
Приведем простейшей пример интегрируемой по Риману функции. 1)Пусть
2)при §2. Условия Th1.(необходимые условия Пусть Доказательство От противного Достаточно доказать, что если (см. необходимые условия Возмем некоторое Þ неограниченность хотя бы на одном отрезке Пусть ( для определенности ) Выберем производные точки
Точку Т.к
Т.О.
Где
Составим интегральную сумму :
Тогда
Замечание .из ограниченности функции Доказательство . Доказательство проведем от противного : Пусть
тогда для любого Теперь , за счет выбора (.) Тогда и вся сумма Это противоречит тому, что при мелких разбиениях интегральная сумма близка к определенному числу J(интегралу).
Замечание. Ограниченность – необходимое , но не достаточное условие интегрируемости. Рассмотрим пример ограниченной , но не интегрируемой функции Пусть функция
Q-множество рациональных чисел Очевидно И тогда
А можно выбрать все
Поэтому не
Пусть далее f-определена и ограничена на
Обозначим :
Составим суммы:
Обозначаем:
Þ
Очевидно
Но Т.е. Т.е. Можно определить.
Т.к. Т.е . Геометрическая интерпретация ограничевается случаем , когда Число Число Верхняяя и нижняя суммы Неравенства (*) обозначают , что площади ступенчатого входящего и выходящего многоугольников (при любом разбиениеи) заключены между площадями входящего и выходящего прямоугольников. Тогда можно определить:
Обозначим:
Th2(Теорема Дарбу – необход. И дост-ая усл-е Пусть f(x) – определена и ограничена на [a,b] Тогда 1. 2. 3. При этом Th3. (Достаточное усл-е инт-сти для непрерывных функций) Пусть (б/д) Th4. (Дост-ое усл-е инт-ти для кусочно-непрерывных функций) Пусть f(x) – ограничена на [a,b] и имеет лишь конечно число точек разрыва на [a,b] =>
Th5. (Достаточное условие интегр-ти монотонных функций) Пусть f(x) – определена и монотонна на [a,b] => (б/д) Отметим, что в th5 в неявном виде заложено условие ограниченности функции f(x) на [a,b] |
|
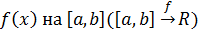
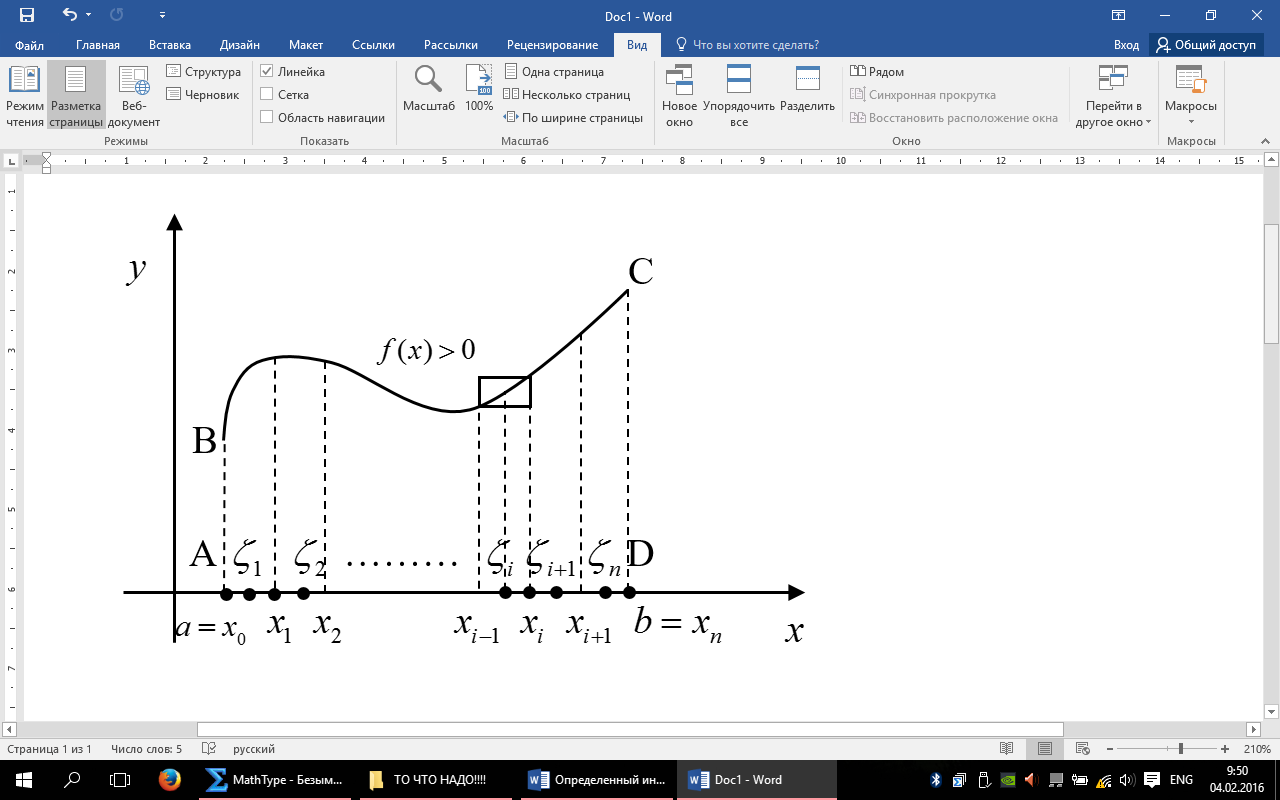
 ,
, , с боков прямыми
, с боков прямыми  , а снизу отрезком оси ОХ.
, а снизу отрезком оси ОХ. ) основание трапеции произвольным образом на «n» частей точками
) основание трапеции произвольным образом на «n» частей точками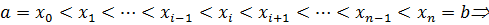
 по
по 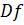
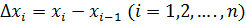
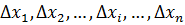
 выберем точки
выберем точки 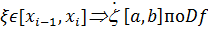 т.е.
т.е. (cовокупность (…) {
(cовокупность (…) {  } назовем размеченым разбиением [a,b])
} назовем размеченым разбиением [a,b])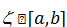
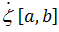
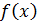 в этих (…)(3)
в этих (…)(3)
 .
.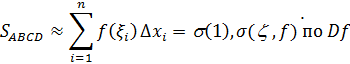
 и увеличивать число точек , то при некоторых свойствах функции
и увеличивать число точек , то при некоторых свойствах функции 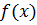 в пределе получим площадь криволинейной трапеции , т.е
в пределе получим площадь криволинейной трапеции , т.е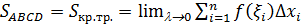 , где
, где  -шаг разбиения.
-шаг разбиения.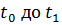
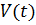 .
. называются интегральной суммой
называются интегральной суммой  (сумма Римана)
(сумма Римана)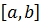 и выбора (…)
и выбора (…)  .
.
 }
}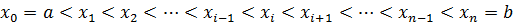
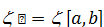 (зет готическое)
(зет готическое) длина отрезка [
длина отрезка [ 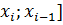
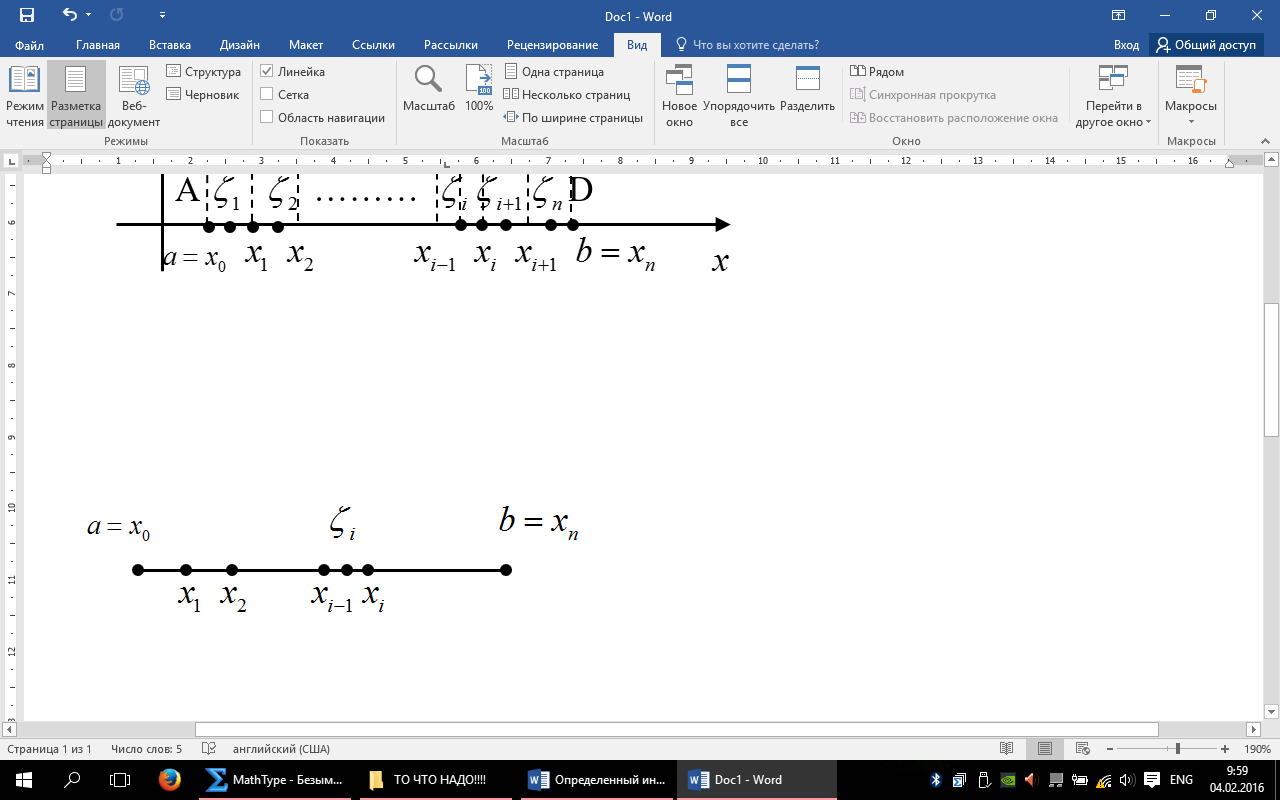
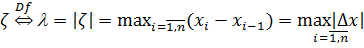
 к которому добавлен набор точек
к которому добавлен набор точек 
 i=1,2,…,n.
i=1,2,…,n.
 можно сделать бесконечно мног пунктированных разбиений
можно сделать бесконечно мног пунктированных разбиений 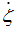 .
.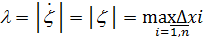
 Фиксируем некоторое пунктированное разбиение отрезка
Фиксируем некоторое пунктированное разбиение отрезка  .
. -называется интегральной суммой Римана. (простой интегральной суммой)
-называется интегральной суммой Римана. (простой интегральной суммой) -числовая функция , аргументами которой являются функция
-числовая функция , аргументами которой являются функция  , определенная на
, определенная на 
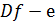 предела таких функций .
предела таких функций .


 остаются в силе свойства пределов.
остаются в силе свойства пределов. конечного предела:
конечного предела: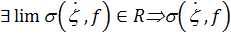 – ограничена на (
– ограничена на (  Определенного интеграла (интеграла Римана)
Определенного интеграла (интеграла Римана)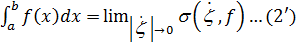 ,если последний
,если последний  и конечный.
и конечный. подынтегральная функция .
подынтегральная функция . зависит от переменно «x» являющейся «немой» переменной (в то время , как неопределенный интеграл
зависит от переменно «x» являющейся «немой» переменной (в то время , как неопределенный интеграл  зависит от
зависит от  ).
).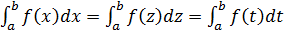 и тд.
и тд. , не зависящий ни от способа деления отрезка [a,b] на части , ни от выбора точек
, не зависящий ни от способа деления отрезка [a,b] на части , ни от выбора точек 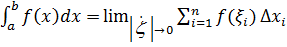
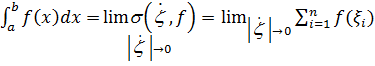
 определиние интеграла Романа
определиние интеграла Романа Число
Число  называется пределом интегральных сумм если для
называется пределом интегральных сумм если для 
 -м способе разбиение [a,b] , при котором
-м способе разбиение [a,b] , при котором  и при
и при 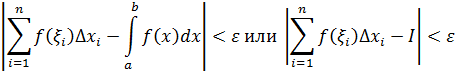
 Если
Если  называется интегрируемой(интегрируемой по Римано) на[a,b].
называется интегрируемой(интегрируемой по Римано) на[a,b].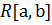
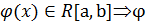 - интегрируемая на [a,b]
- интегрируемая на [a,b] и
и  ,то
,то 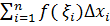 имеет простой геометрический смысл:
имеет простой геометрический смысл: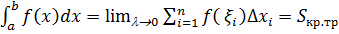 можно рассматривать как «площадь» этой криволинейной трапеции.
можно рассматривать как «площадь» этой криволинейной трапеции.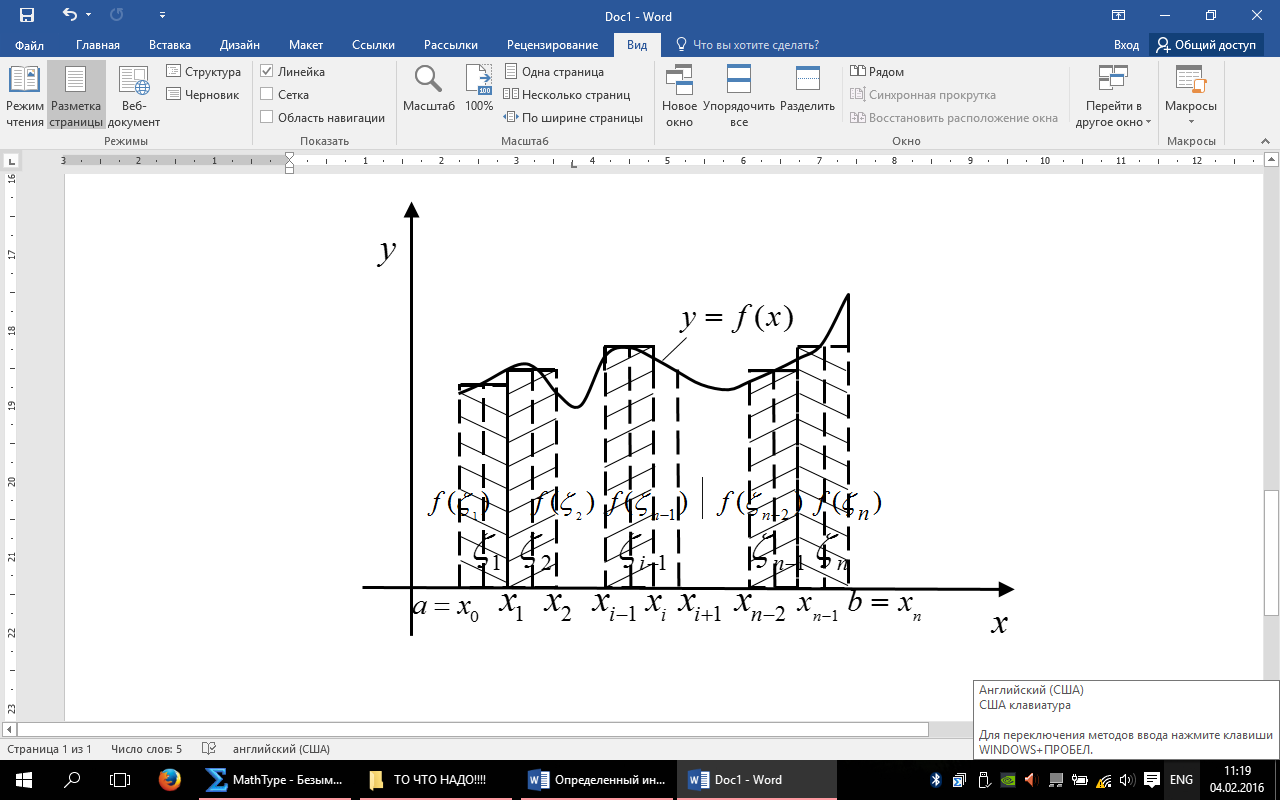
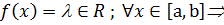
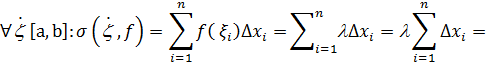
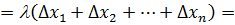
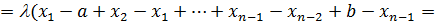
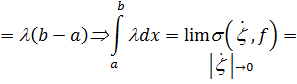
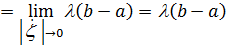
 Заметим ,что, как правило определеный интеграл с помощью данного определения не вычисляют.
Заметим ,что, как правило определеный интеграл с помощью данного определения не вычисляют.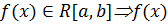 ограничена на
ограничена на 
 т.е
т.е  конечный
конечный  . Для этого достаточно доказать
. Для этого достаточно доказать неограничена на множестве разбиений , т.е.
неограничена на множестве разбиений , т.е.  ;
; 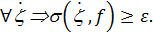
 т.к
т.к 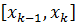 .
. - неограничена на
- неограничена на 
 найдем следующем образом:
найдем следующем образом: -неограниченная на
-неограниченная на  ,что
,что 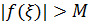
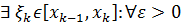
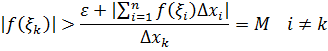
 получили пунктированое разбитие
получили пунктированое разбитие 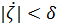

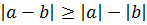
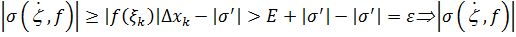 –не ограничена на
–не ограничена на  -противоречие. Отметим , что условие th является лишь необходимым но не достаточным :
-противоречие. Отметим , что условие th является лишь необходимым но не достаточным :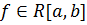
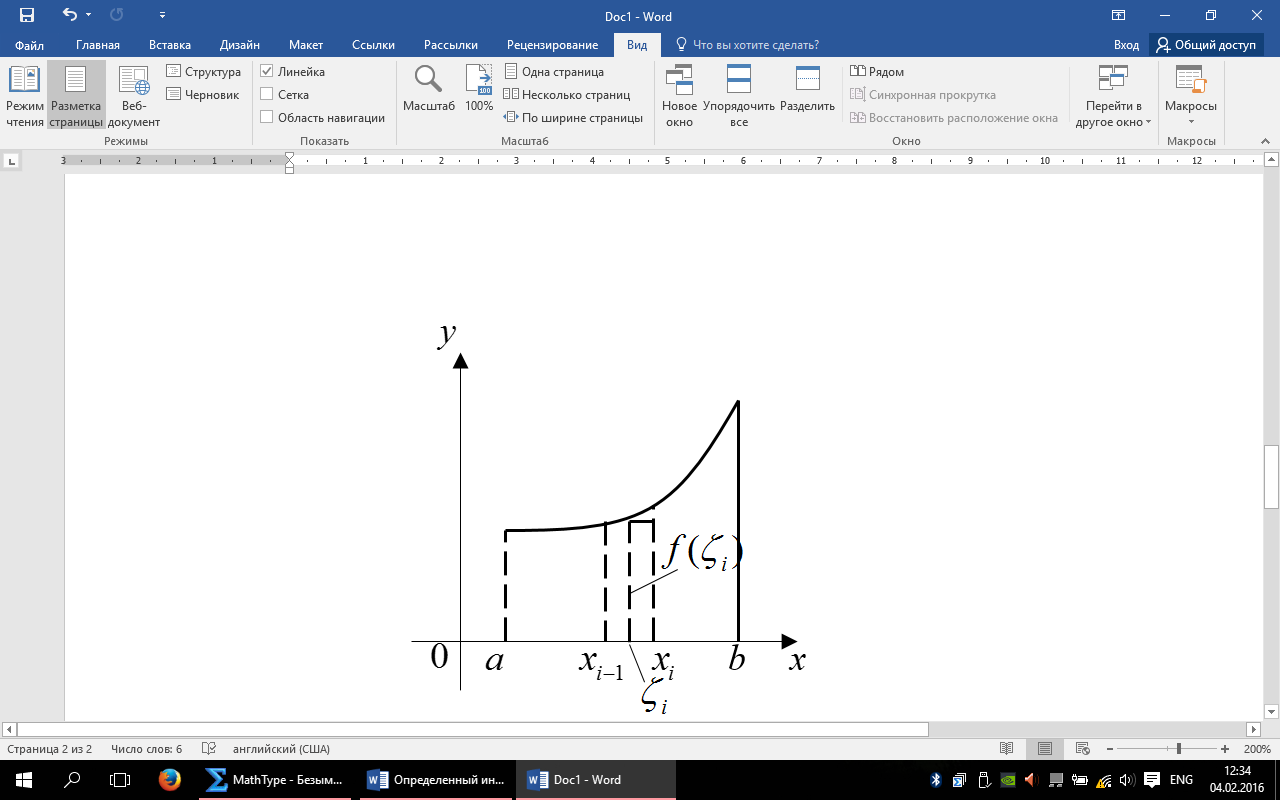
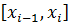 на котором функция не ограничена . Для случая изображенного на рисунке , это отрезок
на котором функция не ограничена . Для случая изображенного на рисунке , это отрезок 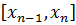
 , произвольно большим ( не меняя других слагаемых ).
, произвольно большим ( не меняя других слагаемых ).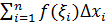 будет большой , не зависимо от мелкости разбиения.
будет большой , не зависимо от мелкости разбиения.
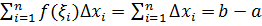
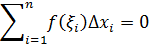
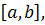
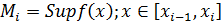
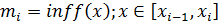
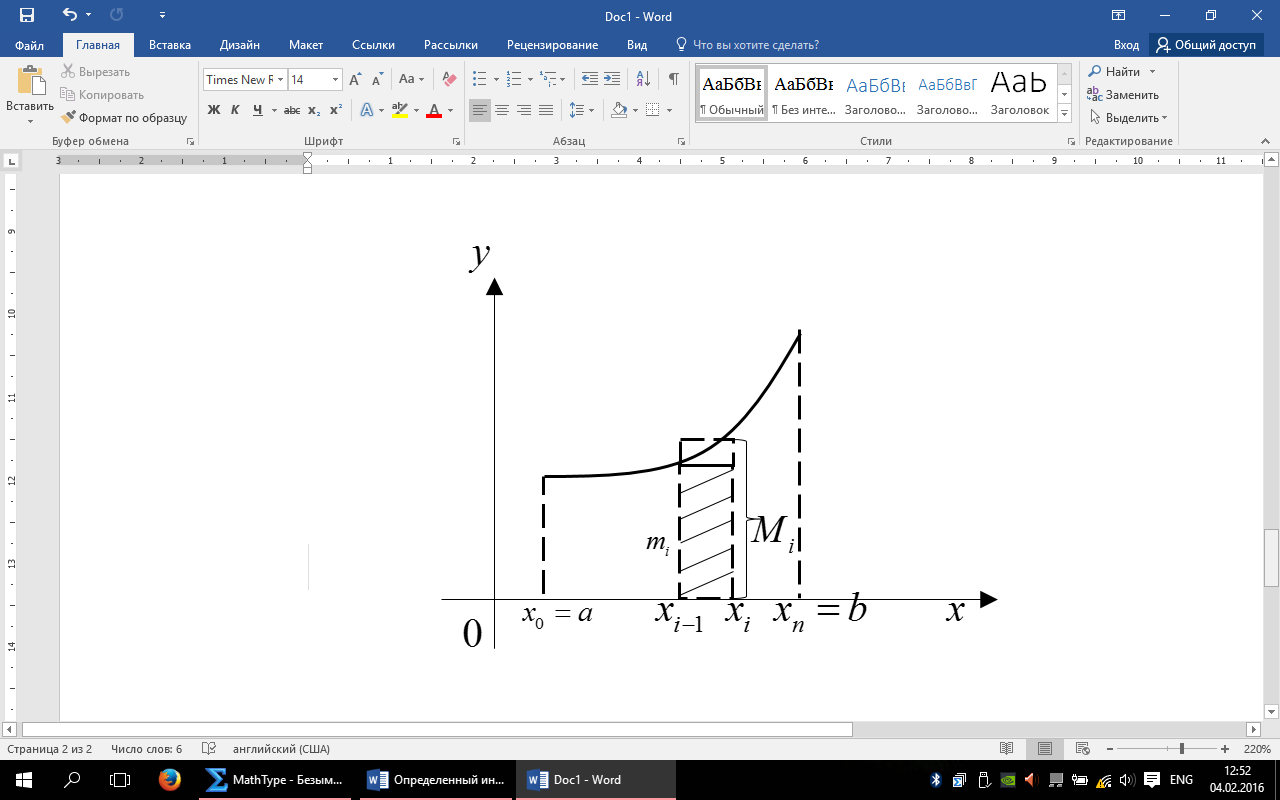
 – верхняя сумма Дарбу.
– верхняя сумма Дарбу.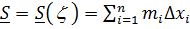 – нижняя сумма Дарбу.
– нижняя сумма Дарбу.
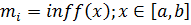
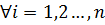
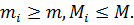
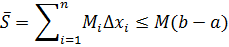

 Þ
Þ 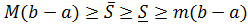
 -ограничены ,
-ограничены ,  - огранечены .
- огранечены . (*)
(*)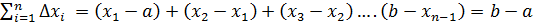
 -ограничены ,
-ограничены ,  - огранечены .
- огранечены .
 выражает площадь выходящего прямоугольника с основанием
выражает площадь выходящего прямоугольника с основанием  есть площадь выходящего прямоугольника. Из всех прямоугольников с основанием
есть площадь выходящего прямоугольника. Из всех прямоугольников с основанием  суть площади ступенчатых-входящего и выходящего – многоугольников , построенных для данного разбиения
суть площади ступенчатых-входящего и выходящего – многоугольников , построенных для данного разбиения  .
. - верхний интеграл Дарбу
- верхний интеграл Дарбу - нижний интеграл Дарбу
- нижний интеграл Дарбу - колебание f на
- колебание f на 


 )
) ó выполняется одно из трех эквивалентных условий:
ó выполняется одно из трех эквивалентных условий: (верхний интеграл Дарбу = нижнему)
(верхний интеграл Дарбу = нижнему) где
где  =
= 



 (б/д)
(б/д)