|
|
Площадь поверхности вращения.Опр-й ин-л может быть в ряде случаев применен и к вычислению площади поверхности вращения. R +vqXVs+2DooEoTzLLacd+ZjhIHW3b35JTr+D1/O/wvQ3AAAA//8DAFBLAwQUAAYACAAAACEAK9A9 lOAAAAALAQAADwAAAGRycy9kb3ducmV2LnhtbEyPwU6DQBCG7ya+w2ZMvNkFGqkgS2Oa2IvxYDV6 HdgtENhZwm4p+vSOJ3uc+b/8802xXewgZjP5zpGCeBWBMFQ73VGj4OP9+e4BhA9IGgdHRsG38bAt r68KzLU705uZD6ERXEI+RwVtCGMupa9bY9Gv3GiIs6ObLAYep0bqCc9cbgeZRFEqLXbEF1ocza41 dX84WQWv+LkP89LX+3486i87Vrv1z4tStzfL0yOIYJbwD8OfPqtDyU6VO5H2YlCwSZOYUQ7idQaC iSxKeVMpSO43GciykJc/lL8AAAD//wMAUEsBAi0AFAAGAAgAAAAhALaDOJL+AAAA4QEAABMAAAAA AAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQSwECLQAUAAYACAAAACEAOP0h/9YAAACU AQAACwAAAAAAAAAAAAAAAAAvAQAAX3JlbHMvLnJlbHNQSwECLQAUAAYACAAAACEACMslREICAABd BAAADgAAAAAAAAAAAAAAAAAuAgAAZHJzL2Uyb0RvYy54bWxQSwECLQAUAAYACAAAACEAK9A9lOAA AAALAQAADwAAAAAAAAAAAAAAAACcBAAAZHJzL2Rvd25yZXYueG1sUEsFBgAAAAAEAAQA8wAAAKkF AAAAAA== " filled="f" stroked="f" strokeweight=".5pt">

Площадью поверхности, полученной от вращения дуги вокруг какой-нибудь оси наз-ся предел площади поверхности полученной от вращения ломанной вписанной в дугу при неограниченной размельчении ее звеньев (поверхность от вращения ломанной вокруг оси состоит из конечного числа боковых поверхностей усеченных конусов и понятия площади такой поверхности дается в элементарной геометрии). Так,например:
Предположим известной ф-лу для площади поверхности усеченного конуса. Пусть P-поверхность получаемая при вращении вокруг оси. Абсциссы кривой
Площадь Р можно определить следующим образом. Пусть Тогда при вращении наряду с Р получим поверхность
Df Если ThПусть Док-во. Для По th Коши о промежуточном значении. Сформулируем ее.
А по th Лагранжа
Тогда
Положим Эта сумма Которая в силу сделанных предположений о ф-ии f(x) непрерывна а потому и интегрируема на [a,b]. (т.е т.к Следовательно
Оценим отклонение интегральной суммы
1. из th
2. Из непрерывности производной ф-ии
Это число сколь угодно малое. Тогда Перепишем ее так.
Где dl-диф-л дуги. Замечание. А) если кривая АВ задана параметрическими ур-ями:
Тогда Т.е
Б) Если АВ задана ур-ем в полярной системе координат.
Вычисление объемов тел V. Df Ограниченным телом будем наз-ть Df Тело V кубируемо (имеет объем) если верхняя грань w – вписанный многогранник в V W – описанный –“-“- - Объем V обозначается Утверждение 1. Тело V кубируемо ó, когда
При этом (б/д) Утверждение 2. Если Объем тела с известными площадями поперечных сечений.
Рассмотрим тело Т содержащееся между плоскостями
Предположим, что всякое сечение S(x) тела Т плоскости, перпендикулярной к оси ОХ в (.) Th Если тело Т кубируемо, а ф-я S(x)
Объём тела вращения Простейшее тело – тело вращения либо криволинейной трапеции, либо криволинейного сектора.

Vx – вращение вокруг оси oxVy – вращение вокруг оси oy
Th1: Тело вращения Vx криволинейной трапеции 1-го рода (типа)
Имеет объём (кубируемо)
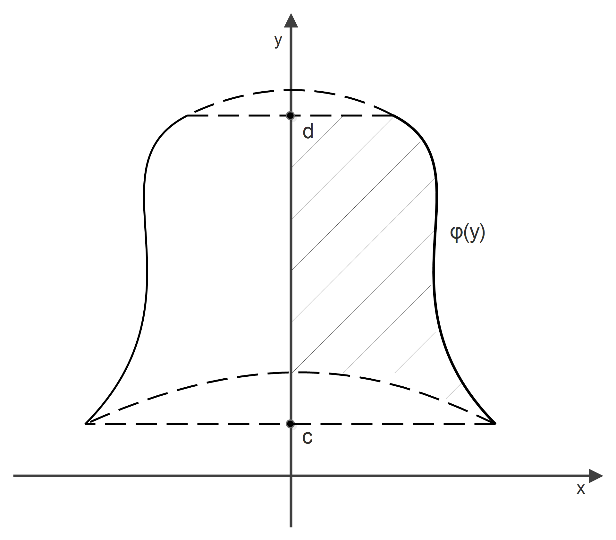
Th2: Тело вращения Vy – кубируемо и
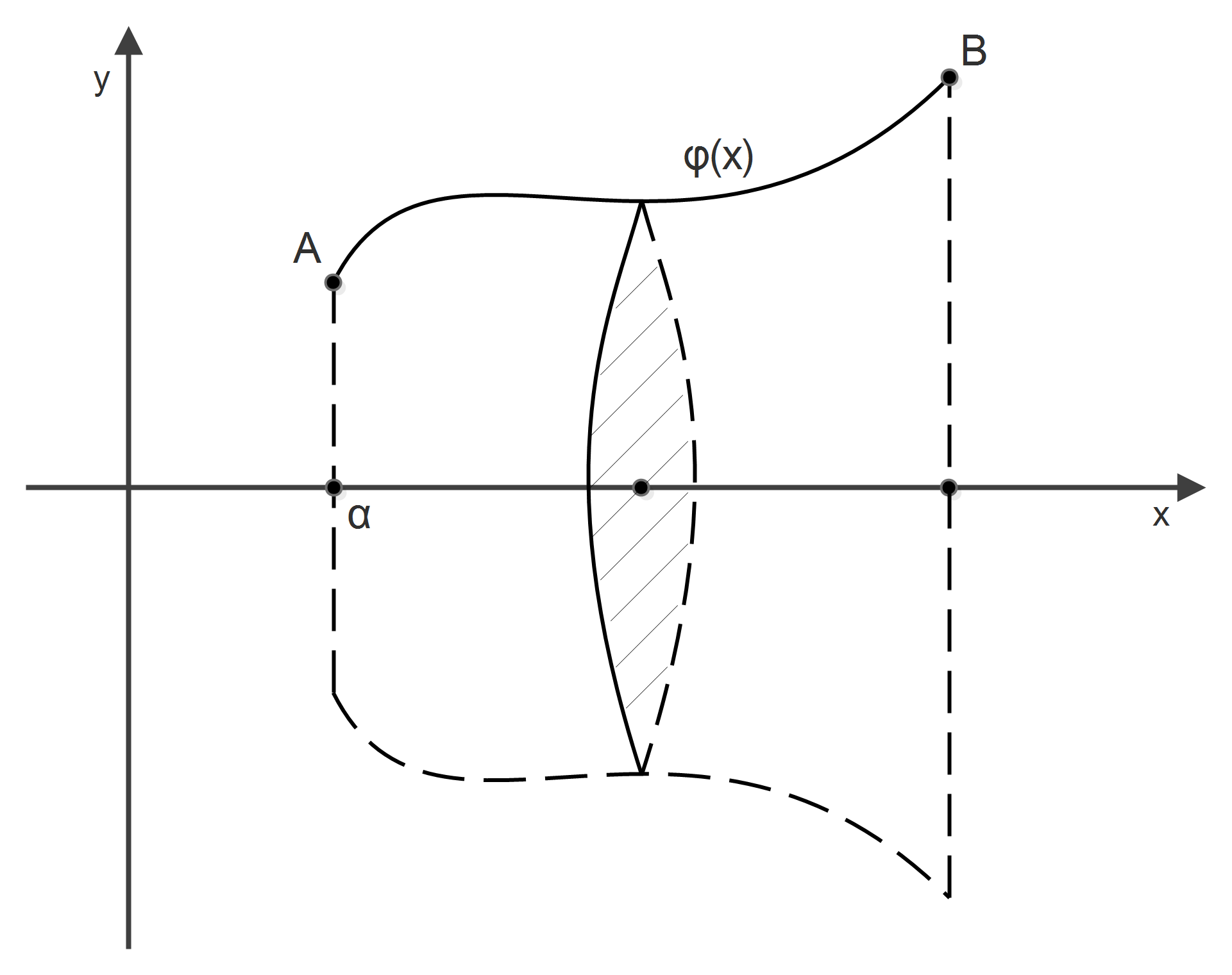
Пусть вокруг оси ox вращается криволинейная трапеция, ограниченная осью ox, прямыми x=a, x=b и дугой AB: Эта трапеция при вращении вокруг оси ox опишет тело, являющееся телом вращения, т.к. каждая точка дуги AB описывает окружность, центр которой лежит на оси ox, то площади поперечных сечений нам известны для любого x.
Замечание 1: Если вращение тела образуется вращением криволинейной трапеции относительно оси oy, то
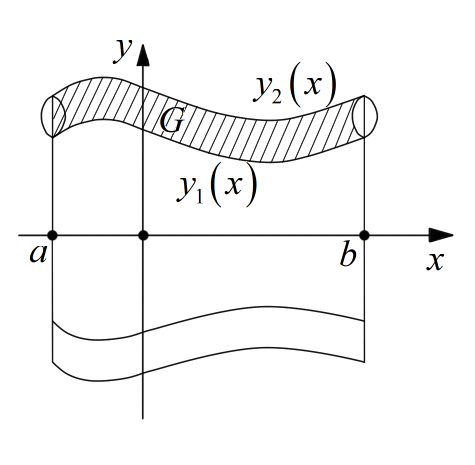
Замечание 2: Пусть То объём V тела образованного вращением фигуры G, ограниченной графиками функции y1(x) и y2(x) и отрезками x=a и x=b, равен
Для тел, образованных вращением фигуры G вокруг оси oy при аналогичных предположениях относительно данных функций, верны, соответственно, следующие формулы:
Если тело образовано вращением области G вокруг оси, не пересекающей область G и не являющейся одной из осей координат, то для вычисления обхёма полученного тела делают замену системы координат так, что чтобы в новой системе одна из координатных осей совпадала с осью вращения. В частности: А) Если осью вращения является прямая y=l, не пересекающая область то объём |Vl| тела Vl , полученного вращением G вокруг этой оси, вычисляется по формуле Б) Если осью вращения является прямая x=l, не пересекающая область то объём |Vl| тела Vl , полученного вращением G вокруг этой оси, вычисляется по формуле Обе эти формулы получаются переносом осей координат так, чтобы в первом случае ось l стала новой осью OX1, а во второй – ось l стала новой осью OY1.
|
|






 - площадь сферы радиуса r.
- площадь сферы радиуса r. - боковая поверхность цилиндра с высотой H и радиусом r.
- боковая поверхность цилиндра с высотой H и радиусом r. - боковая поверхность усеченного конуса с радиусами оснований R и r. И длиной образующей l.
- боковая поверхность усеченного конуса с радиусами оснований R и r. И длиной образующей l.
 - некоторое разбиение отрезка
- некоторое разбиение отрезка  [a,b]. Для каждой пары точек
[a,b]. Для каждой пары точек  и
и  соединим отрезком прямой точки
соединим отрезком прямой точки  и
и 
 составленную из усеченных конусов площадь.
составленную из усеченных конусов площадь.
 конечный предел
конечный предел  то этот предел называется площадью поверхности Р.
то этот предел называется площадью поверхности Р. , тогда поверхность Р-имеет площадь определяемую формулой
, тогда поверхность Р-имеет площадь определяемую формулой 
 с
с 

 тогда
тогда 






 - эта сумма не является интегральной.
- эта сумма не является интегральной. .
. является суммой Римана для ф-и
является суммой Римана для ф-и 


 от суммы
от суммы  .
.

 - равномерно непрерывна
- равномерно непрерывна
 на [a,b] => непрерывность, а следовательно и ограниченность на этом отрезке функции
на [a,b] => непрерывность, а следовательно и ограниченность на этом отрезке функции  .
. т.е
т.е  тогда
тогда

 в
в 

 .
.  имеют непрерывные пр-ные на [
имеют непрерывные пр-ные на [  ,
,  ]
]






 где
где  -можно считать параметром.
-можно считать параметром. тогда
тогда 
 ограниченную замкнутую область в
ограниченную замкнутую область в  .
.
 и
и 


 равен каждому из этих объемов
равен каждому из этих объемов - разбиение V
- разбиение V  два объема из трех
два объема из трех  ,
,  ,
,  то
то  объем 3-го тела и имеет место равенство
объем 3-го тела и имеет место равенство  . б/д
. б/д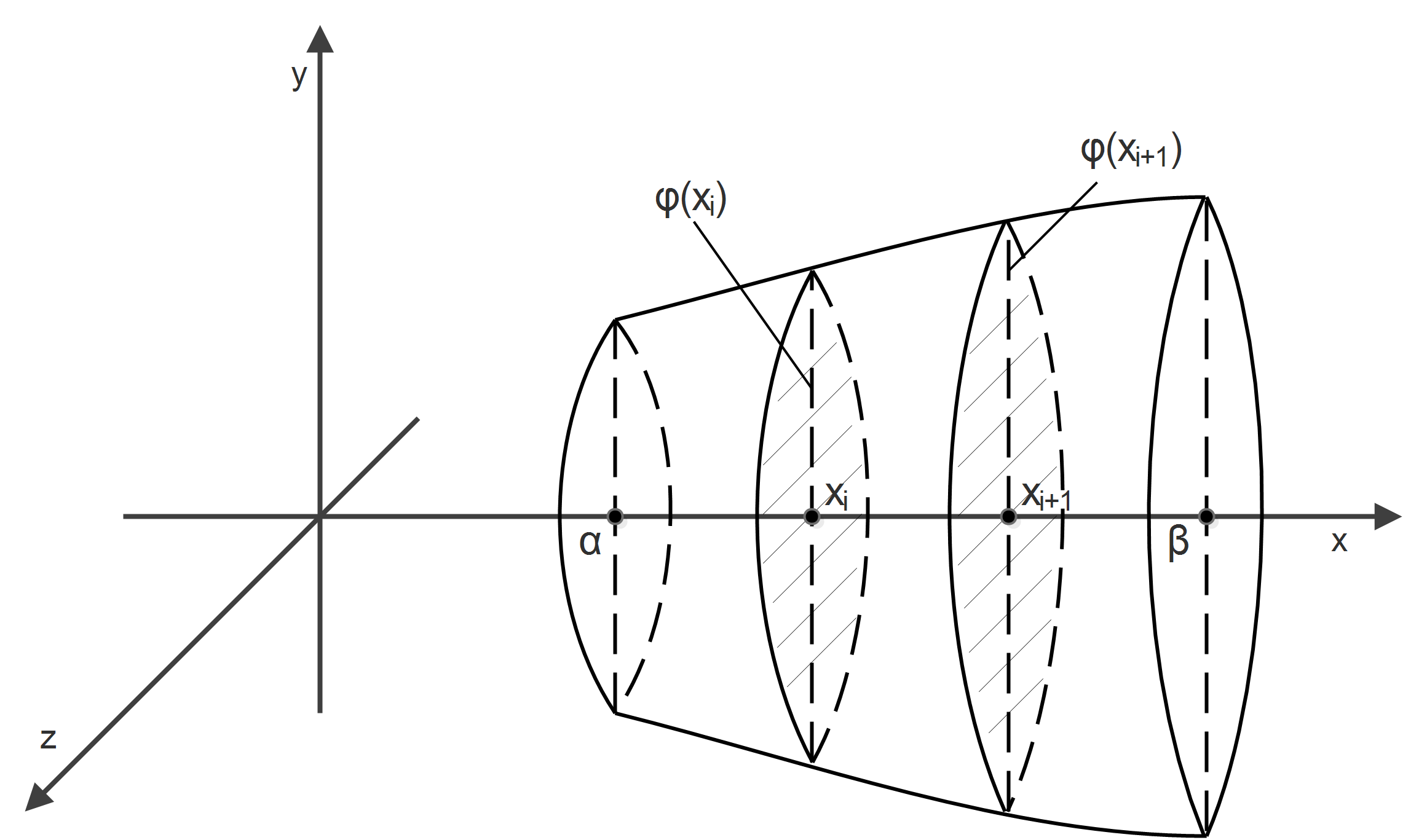

 , есть квадрируемая плоская фигура, площадь которой S(x) известна.
, есть квадрируемая плоская фигура, площадь которой S(x) известна.
 интегрируема на [a,b]
интегрируема на [a,b]  то объем |V| тела Т можно вычислить по формуле
то объем |V| тела Т можно вычислить по формуле …(1)
…(1)
 .
. .
.
 , где
, где  ,
,  ,
,  .
. . Применив формулу
. Применив формулу  , получим:
, получим: 
 .
.

 ,
,  ,
,

 ,
, .
. ,
, .
.


