|
|
Определенный интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.Мы рассматривали интегралы с постоянными пределами интегрирования Величина такого интеграла для данной подынтегральной функции зависит только от пределов интегрирования “a” и “b” и не зависит от x. Если менять, например, верхний предел “b”, то величина интеграла станет некоторой функцией от переменной “x”. Df1 Пусть С переменным верхним пределом интегрирования. Обозначим переменную интеграла в Аналогично Рассмотрение ин-ла Относительно этой функции докажем следующие теоремы. Th1 (о непрерывности определенного интеграла Римана как функции верхнего предела)
Док-во Пусть
Отсюда:
Но т.к Th2 (Диф-ность (О диф-ти О.И.Римана, как функции верхнего предела)
Док-во Изth1 известно, что Применим к ин-лу (1) th-му о среднем, т.е Найдем производную функции
Т.к th доказана.
Т.О. если По его переменному верхнему пределу x на этом сегменте Тогда => th-мы. Th a) Если Является первообразной для ф-и f(x) на этом сегменте ([a,b]). Th б) Объяснение.
В равенстве (*) использована непрерывность: Если
Что
Когда
Замечание. Если x=”a” или “b”, то под Следствие 1) 1. 2. Док-во (1) следует из th2 т.к f(x) – непрерывна Пункт (2) Первообразная действительно В равенстве (*) использована непрерывность: если Так как f непрерывная функция, то отсюда следует, что Итак, Например Отметим, что теорема 2 доказывает фактически
Т.к операция интегрирования есть обратная к диф-нию. Кроме того доказана связь неопределенного интеграла и определенного
Следствие 2
Доказательство
Т.к. Т.к. Th 3 Основная теорема интегрального исчисления Пусть
Формула Ньютона-Лейбница Для обозначения разных Доказательство
Если Th Для того чтобы вычислить Теперь мы имеем правила вычисления Доказательство По следствию (1) теоремы 2
Пусть х=а Т.е. Пусть Пример
Формула Формула Ньютона-Лейбница С помощью символа подстановки Формула (2) устанавливает зависимость между определённым и неопределенными интегралами функций §5 Замена переменной в определенном интеграле. Интегрирование по частям Теорема 1 Пусть 1. 2. 3. 4.
Тогда Доказательство
Т.к.
По теореме о замене переменной в неопределенном интеграле
Отсюда Отметим, что при В случае, если
При некоторых t,
Пример
Этот интеграл можно вычислить и без теоремы 1
Нам известен неопределенный интеграл
(По формуле |
|
 , где a и b – const
, где a и b – const

 буквой t, чтобы не смешивать ее с верхним пределом x, т.е
буквой t, чтобы не смешивать ее с верхним пределом x, т.е  .
.
 - интеграл с переменным нижним пределом.
- интеграл с переменным нижним пределом.  как функции нижнего предела не представляет специального интеграла, т.к в силу свойств интеграла
как функции нижнего предела не представляет специального интеграла, т.к в силу свойств интеграла  Задача свелась к изучению интеграла как функции верхнего предела.
Задача свелась к изучению интеграла как функции верхнего предела.
 имеем, в силу аддитивности интеграла Римана
имеем, в силу аддитивности интеграла Римана 


 - ограничена на [a,b] , т.е
- ограничена на [a,b] , т.е 




 ч.т.д
ч.т.д ) (2й вариант док-ва)
) (2й вариант док-ва)

 и
и  (1),
(1), 


 …(*)
…(*) , то
, то  или
или 

 - есть первообразная, для f(x) на [a,b].
- есть первообразная, для f(x) на [a,b]. , то
, то  (инт.
(инт.  )
) и равна значению f(x) подынтегральной функции f(t) при t=x
и равна значению f(x) подынтегральной функции f(t) при t=x , то ф-я
, то ф-я  ,
,  .
. - ф-я имеет на ней первообразную.
- ф-я имеет на ней первообразную.

 , а значит
, а значит . Т.к f-непр. Ф-я, то отсюда =>,
. Т.к f-непр. Ф-я, то отсюда =>, . Или
. Или 
 th доказана.
th доказана.
 тогда
тогда  , то
, то  .
. следует подразумевать односторонние производные.
следует подразумевать односторонние производные.
 есть первообразная для f(x) на [a,b]
есть первообразная для f(x) на [a,b] первообразная для f(x) на [a,b]
первообразная для f(x) на [a,b] .
. .
. , то
, то  , а значит и
, а значит и  .
. .
. , th-ма доказана.
, th-ма доказана. .
. следующую формулу.
следующую формулу.

 для
для 



 и
и  - первообразная на
- первообразная на  для
для  , тогда
, тогда
 удобно использовать так называемый знак подстановки
удобно использовать так называемый знак подстановки 
 -е две переменные функции f(x) заданой на [a,b], отличаются на постоянную
-е две переменные функции f(x) заданой на [a,b], отличаются на постоянную , а
, а  другая первообразная непрерывной функции f(x), то
другая первообразная непрерывной функции f(x), то  , т.е.
, т.е.  положим в формуле х=а, а затем х=b. Как нам известно
положим в формуле х=а, а затем х=b. Как нам известно  для
для  -й функции, принимающей конечное значение в (.) а. Поэтому
-й функции, принимающей конечное значение в (.) а. Поэтому 
 по
по  от
от  , следует вычислить значение произвольной ее первообразной в (.) «
, следует вычислить значение произвольной ее первообразной в (.) «  » и в (.) «
» и в (.) «  » и вычесть из первого значения второе
» и вычесть из первого значения второе - первообразная
- первообразная  на
на  . Т.о.
. Т.о.  - две первообразные
- две первообразные 



 (*)
(*) в(*)
в(*) 


 формулу (1) запишем в виде
формулу (1) запишем в виде  …(2)
…(2) , множество (…) разрыва которой не более чем счетно, выражаемую формулой
, множество (…) разрыва которой не более чем счетно, выражаемую формулой  (3)
(3)




 (1)
(1)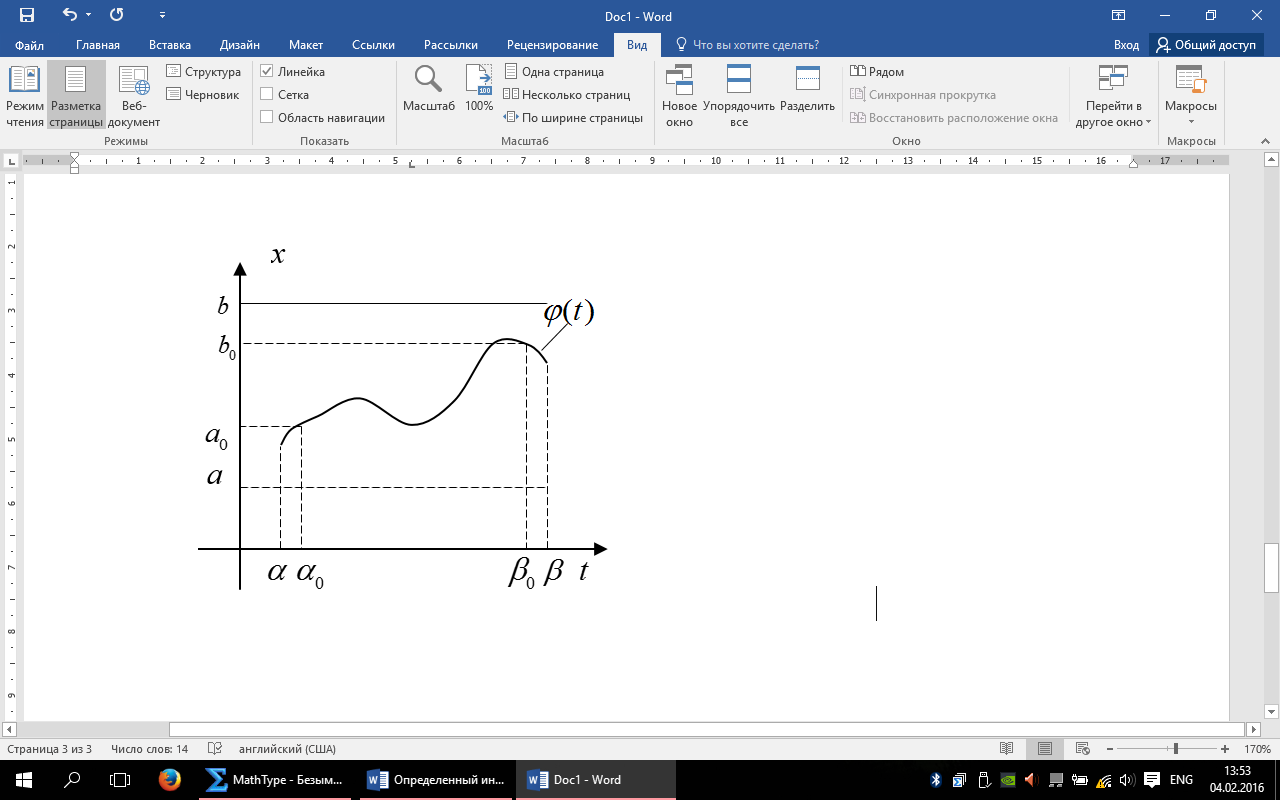
 -первообразная на
-первообразная на  и
и 

 -первообразная для
-первообразная для  на
на  (и на
(и на  )
)
 (1)
(1) в доказательстве должны фигурировать соответствующие односторонние производные.
в доказательстве должны фигурировать соответствующие односторонние производные.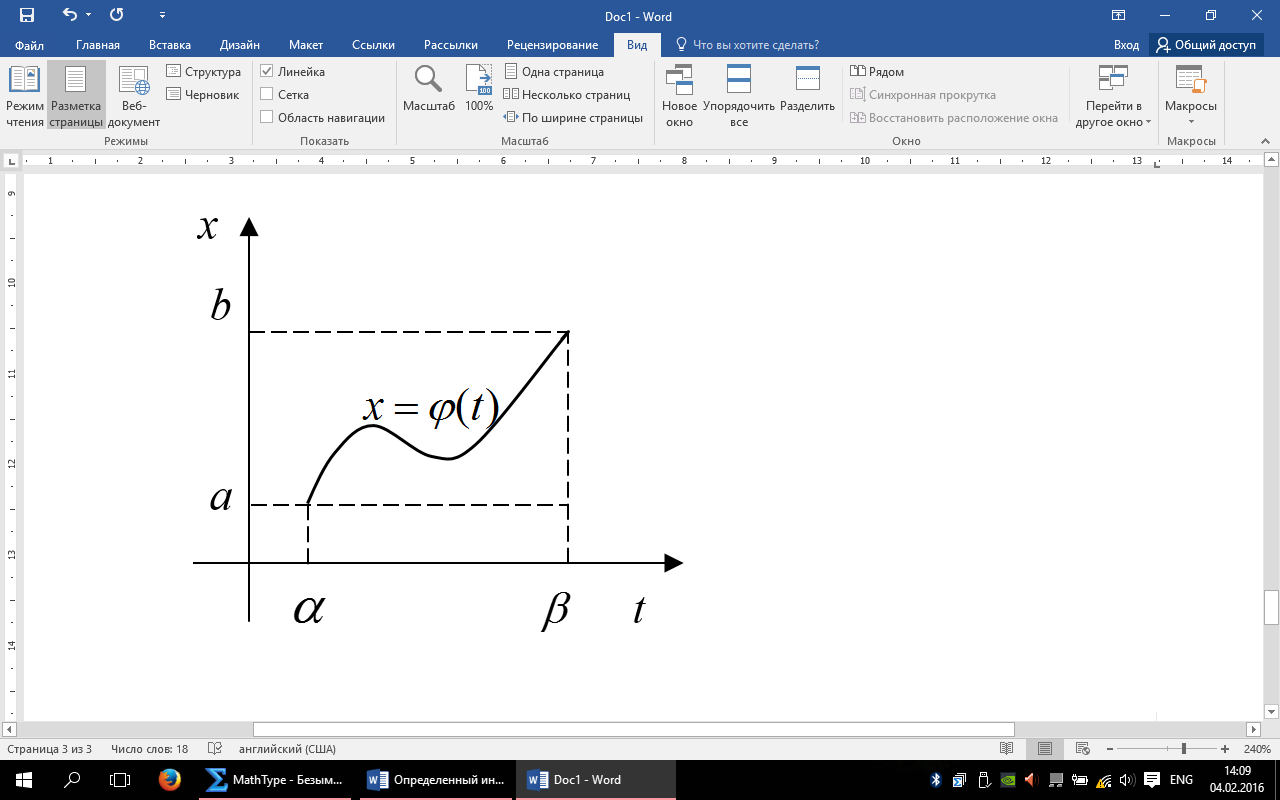


 может выходить за отрезок
может выходить за отрезок  . Но обязательно
. Но обязательно 

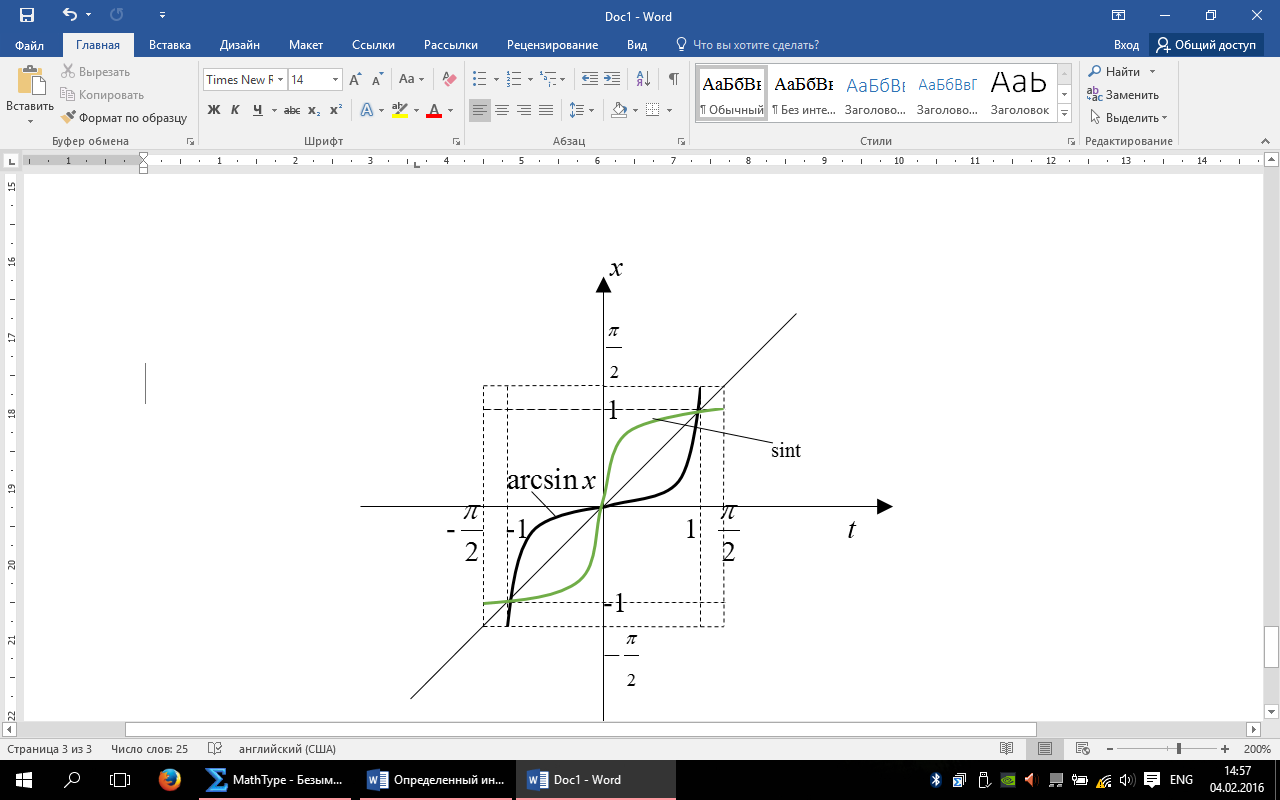


 )
)