|
|
Индукция магнитного поля соленоидаДля создания магнитного поля в технике используется соленоид – цилиндрическая катушка, состоящая из большого числа витков, равномерно намотанных на общий сердечник (рис. 4.5). Рассмотрим соленоид длиной L, имеющий N витков, по которому течет ток I. Длину соленоида считаем во много раз большей диаметров его витков. Магнитное поле такого соленоида целиком сосредоточено внутри него и однородно. Снаружи соленоида поле мало и его практически можно Величину индукции магнитного поля соленоида можно найти, складывая магнитные индукции полей, создаваемых каждым витком соленоида. Так как витки соленоида намотаны вплотную друг к другу, на длине dx сосредоточено
Суммарное поле:
При интегрировании соленоид считаем бесконечным. Как видно из (4.9) магнитное поле соленоида зависит от плотности намотки – числа витков на единицу длины соленоида
Магнитный поток
dФ = ВndS = Bcos α × dS, (4.10) где Вn – проекция вектора В на направление, перпендикулярное к площадке dS; α – угол между вектором нормали nи вектором В. Положительное направление нормали связано правилом правого винта с током, текущим по контуру, ограничивающему площадку dS. Магнитный поток Ф через произвольную поверхность S можно представить в виде:
Действие магнитного поля на заряды На электрический заряд q, движущийся в магнитном поле с индукцией В со скоростью V, действует сила Лоренца:
Абсолютная величина магнитной силы: F = qvB Sin α ,
По правилу векторного произведения магнитная сила Fперпендикулярна плоскости, в которой лежат вектора Vи B. Если q>0, магнитная сила Fсовпадает с направлением векторного произведения [V,B], если q<0, то противоположно. Для положительного заряда, движущегося в магнитном поле, как показано на рисунке 4.6, сила F направлена вдоль отрицательного направления оси Z. Продольная компонента скорости Vll под действием магнитного поля изменяться не будет и движение заряженной частицы вдоль оси Х – равномерное. Результирующее движение частицы – по винтовой линии (рис.4.6). Спираль может быть как правой, так и левой в зависимости от знака заряда q. Радиус спирали R найдем из условия, что при равномерном движении частицы по окружности сила Fявляется центростремительной силой:
где m – масса заряженной частицы. Отсюда:
Время, за которое частица совершит полный оборот (период):
Из формулы (4.13) следует, что период обращения частицы не зависит от ее скорости. Однако надо помнить, что этот вывод справедлив только при условии V<<c, где: с – скорость света. Если движение частицы происходит как в магнитном поле с индукцией B, так и в электрическом поле с напряженностью Е, то на нее действует обобщенная сила Лоренца:
Электромагнитная индукция Если поток магнитной индукции сквозь контур изменяется со временем, то, согласно закону электромагнитной индукции Фарадея, в контуре возникает ЭДС индукции: E= – где
Знак (–) означает: индукционный ток всегда имеет такое направление, что создаваемое им магнитное поле стремиться скомпенсировать то изменение магнитного потока, которым вызван данный индукционный ток (правило Ленца). Ток в замкнутом контуре создает в окружающем пространстве магнитное поле, индукция которого пропорциональна току: В ~I. Поэтому сцепленный с контуром магнитный поток пропорционален силе тока в контуре I: Ф = LI, гдеL–коэффициент пропорциональности называют коэффициентом самоиндукции или индуктивностью контура.
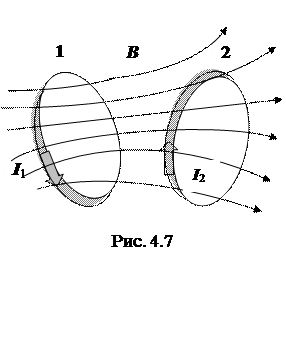
Индуктивность контура L в общем случае зависит от геометрии контура и магнитной проницаемости среды µ. Если эти величины не изменяются, то L = const. Т.е., если контур жесткий и поблизости нет ферромагнетиков, то L = const. Рассмотрим два контура 1 и 2, расположенных на некотором расстоянии друг от друга (рис. 4.7). Если по контуру 1 пропустить ток I1, то он создает поток магнитной индукции через контур 2: Ф21= L21I1. (4.17) Коэффициент пропорциональности L21 называют коэффициентом взаимной индукции контуров (взаимная индуктивность контуров). Он зависит от формы и взаимного расположения контуров 1 и 2, а также от магнитных свойств окружающей среды. При изменении силы тока в первом контуре магнитный поток сквозь второй контур изменяется; следовательно, в нем наводится ЭДС взаимной индукции:
Формула справедлива в отсутствие ферромагнетиков. Если поменять местами контуры 1 и 2 и повторить все предыдущие рассуждения, то получим:
Коэффициенты взаимной индукции равны: L21 = L12 .
|
|
 считать равным нулю.
считать равным нулю. витков. Суммарный ток, протекающий по кольцу, толщиной dx, равен
витков. Суммарный ток, протекающий по кольцу, толщиной dx, равен  . В точке, находящейся на оси соленоида каждое такое кольцо создает магнитное поле, согласно (4.7), равное:
. В точке, находящейся на оси соленоида каждое такое кольцо создает магнитное поле, согласно (4.7), равное: .
. (4.9)
(4.9) .
. Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называется скалярная физическая величина, равная:
Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называется скалярная физическая величина, равная: . (4.11)
. (4.11) . (4.12)
. (4.12) где α – угол между векторами V и В.
где α – угол между векторами V и В. ,
, .
.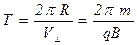 . (4.13)
. (4.13) . (4.14)
. (4.14) , (4.15)
, (4.15)

 Если по контуру протекает изменяющийся со временем ток I(t), то изменяется магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции:
Если по контуру протекает изменяющийся со временем ток I(t), то изменяется магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции: (4.16)
(4.16) . (4.18)
. (4.18) . (4.19)
. (4.19)