|
|
ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО СОПРОТИВЛЕНИЯ НИХРОМОВОЙ ПРОВОЛОКИЦель работы: определение удельного сопротивления нихромовой проволоки при комнатной температуре. Приборы и принадлежности: установка ФПМ 01. Методика эксперимента Известно, что сила тока на участке электрической цепи равна I, сопротивление этого участка R и падение напряжения U, на этом участке, связаны законом Ома: Сопротивление проводника зависит: от материала, из которого изготовлен проводник (от удельного сопротивления ρ), его длины l и площади поперечного сечения S. Эта зависимость представлена соотношением: R = ρ Физическая природа электрического сопротивления проводников, в частности металлов, наглядно объясняется на основе классической теории электропроводности металлов, базирующейся на понятии электронного газа. Сопротивление металлов обусловлено столкновениями электронов с узлами и дефектами кристаллической решетки проводника. Зависимость сопротивления проводников от температуры не может быть объяснена в рамках только классической теории электропроводности металлов. Такое объяснение может быть дано лишь на основе квантовой теории электропроводности металлов, с учетом волновых свойств электронов.
Определение удельного сопротивления проволоки сводится к измерению сопротивления заданного участка проволоки Rпр. с помощью амперметра и вольтметра, измерению его длины l и вычислению площади ее поперечного сечения S. Согласно закону Ома для участка цепи:
Полученное значение сопротивления R представляет собой сумму последовательно соединенных, неизвестного сопротивления Rх и сопротивления миллиамперметра RmA: R = Rx + RmA (2.29) При параллельном соединении неизвестного сопротивления и сопротивления вольтметра RV, неизвестное сопротивление RX определяется соотношением:
Таким образом, определив по соотношению (2.28) общее сопротивление электрической цепи R, и зная сопротивления миллиамперметра RmA и вольтметра RV, можно, используя соотношения (2.29) и (2.30), рассчитать неизвестное сопротивление RX для различных схем включения. Определив неизвестное сопротивление RX, и воспользовавшись соотношением (2.27) можно определить удельное сопротивление проводника:
Длина проволоки l определяется по линейке прибора, площадь поперечного сечения проволоки диаметром d равна
Порядок выполнения работы 1. Установить подвижный контакт, с помощью которого изменяется длина нихромовой проволоки, в среднее положение. 2. В таблицу измерений и вычислений занести длину и диаметр проволоки, параметры измерительных приборов, сопротивление амперметра и вольтметра. 3. Включить кнопку “сеть” на лицевой панели прибора. При этом должна загореться индикаторная лампочка. 4. Кнопки на передней панели прибора поставить в положение В-А и схема.1. 5. Ручкой “регулировка тока” установить значение 50 мА. 6. Измерить напряжение, занести показания амперметра и вольтметра в таблицу. 7. Ручкой “регулировка тока” установить значение сначала 100 мА, затем 150 мА. 8. Для каждого случая измерить напряжение, занести показания миллиамперметра и вольтметра в таблицу 2.7. 9. Кнопку на передней панели прибора поставить в положение схема 2. 10. Выполнить пункты 5-8 для схемы 2. Записать в таблицу 2.8. 11. Используя формулы (2.28) – (2.31) вычислить значения удельного сопротивления. 12. Рассчитать среднее значение удельного сопротивления. 13. Рассчитать абсолютную и относительную погрешность измерений. 14. Сравнить полученный результат с табличным, сделать вывод по результатам исследования. Т а б л и ц а 2.7 Измерения и вычисления для схемы 1
Т а б л и ц а 2.8 Измерения и вычисления для схемы 2
|
|
 (2.26)
(2.26) (2.27)
(2.27) В настоящей работе для определения сопротивления проводников используется установка ФМП 01. На схемах 1 и 2 представлены различные способы подключения вольтметра:
В настоящей работе для определения сопротивления проводников используется установка ФМП 01. На схемах 1 и 2 представлены различные способы подключения вольтметра:

 . (2.28)
. (2.28) (2.30)
(2.30) (2.31)
(2.31)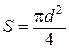 . Расчетная формула для удельного сопротивления примет вид:
. Расчетная формула для удельного сопротивления примет вид: (2.32)
(2.32)