|
|
Определённый интеграл ( ОИ).1. Определённый интеграл как предел как предел интегральных сумм. 2. Теорема о существовании ОИ. Основные свойства ОИ. 3.Геометрический и механический смысл ОИ. 4.Вычисления определённого интеграла: формула Ньютона - Лейбница. 5. Функция верхнего предела и ее свойства. 6. Замена переменной в определённом интеграле. 7. Интегрирование по частям в определённом интеграле. 8. Интегрирование четных и нечетных функций в симметричных пределах. 9.Несобственныей интеграл с бесконечным промежутком (несобственный интеграл I рода) и методы его вычисления. 10.Признаки сходимости несобственного интеграла I рода. 11.Несобственный интеграл от разрывной функции ( несобственный интеграл II рода) и методы его вычисления. 12.Признаки сходимости несобственного интеграла II рода. 13. Приложения определенного интеграла - вычисление площадей плоских фигур. 14. Приложения определенного интеграла - вычисление длины дуги плоской кривой 15. Приложения определенного интеграла - вычисление объема тела 16. Приложения определенного интеграла - вычисление объема тела вращения. 17. Приложения определенного интеграла - вычисление площади поверхности вращения. 18.Механические приложения определенного интеграла(вычисление статистических моментов и координат центра тяжести плоской кривой и фигуры). 19. Приближенное вычисление определенного интеграла: формулы прямоугольников, трапеций и Симпсона. Функции нескольких переменных. 1.Определение функции нескольких переменных (ФНК). Понятие области. Геометрическая интерпретация функции двух переменных. 2.Предел и непрерывность функции нескольких переменных. Свойства функции нескольких переменных в ограниченной замкнутой области. 3.Частные приращения и частные производные функции нескольких переменных. 4.Полное приращение и понятие дифференциала функции нескольких переменных. Формулы вычисления полного дифференциала функции нескольких переменных. 5.Частные производные высших порядков. Теорема о смещенной частной производной. Дифференциал высших порядков и их символическая формула. Раскрыть эту формулу для 6.Формулы вычисления производной сложной функции нескольких переменных в общей форме. Понятие полной производной функции нескольких переменных и формулы его вычисления. 7.Понятие функции нескольких переменных, заданной в неявном виде. Теорема о неявной функции. Формулы вычисления частных производных неявной функции нескольких переменных. Привести простой пример. 8.Скалярное поле. Производная по направлению. Градиент скалярного поля и его свойства. 9.Понятия касательной плоскости и нормали к поверхности функции двух переменных и их формулы. Понятие экстремума функции двух переменных. Теорема о необходимых и достаточных условиях экстремума.
Дифференциальные уравнения 1. Дифференциальные уравнения 1-го порядка Основные понятия .Геометрический смысл ДУ 1-го порядка. 3. Разные формы записи ДУ 1-го порядка и их взаимосвязь(привести простой пример).Определение общего, частного и особого решения ДУ 1-го.Сформулировать задачу Коши. Теорема существования и единственности решения задачи Коши. Геометрическое истолкования решения задачи Коши. Кратные интегралы. 1. Двойной интеграл, его основные свойства. 2.Вычисление двойного интеграла. Замена переменных в двойном интеграле. 3. Тройной интеграл, его основные свойства. 4.Вычисление тройного интеграла. Замена переменных в тройном интеграле. 5.Геометрические приложения кратных интегралов. 6. Применение кратных интегралов для решения задач механики и физики. Криволинейные интегралы. 1.Задачи, приводящие к криволинейным интегралам. Определение криволинейных интегралов первого и второго рода, их основные свойства и вычисление. 2. Геометрические и механические приложения. Связь между криволинейными интегралами первого и второго рода. 3.Формула Грина. Поверхностные интегралы. 1. Определение поверхностных интегралов I и II рода. Их свойства и методы вычисления. 2. Формула Остроградского. Формула Стокса. Вопросы к экзамену(3-й семестр) Тема: «Теория вероятностей». 1.Основные задачи комбинаторики. Определение выборки и её характеристики. Определение выборки без повторения следующих видов: а) размещения из n элементов по k ,б) перестановки из n элементов, в) сочетания из n элементов по k .Привести простые примеры для каждого вида. 2.Основные задачи комбинаторики. Определение выборки и её характеристики. Определение выборки с повторениями следующих видов: а) размещения из n элементов по k, б) перестановки из n элементов, в) сочетания из n элементов по k. Привести простые примеры для каждого вида. 3.Правила умножения и сложения комбинаторики. 4.Определение случайного эксперимента. Определение пространства элементарных событий. Привести примеры. 5. Случайное событие и его вероятность. 6. Случайные события и их классификация. Операции (сложение, умножение, дополнение, разность) над событиями. Основные свойства операций над событиями. 7.Классическая схема определения вероятности. Определение геометрических вероятностей. 8.Определение условий вероятности. Совместность и независимость событий. 9.Общее определение вероятности. Аксиомы теории вероятностей. 10Теорема умножения и сложения вероятностей. 11.Вероятность наступления хотя бы одного из независимых событий. 12.Формула полной вероятности. Формула Байеса. 13.Схема Бернулли – последовательные испытания. Формула Бернулли. Наивероятнейшее число и его вычисление. 14.Определение схемы Бернулли. Условия для приближенного вычисления вероятности согласно формуле Пуассона. Теорема или формула Пуассона. 15.Определение схемы Бернулли. Условия для приближенного вычисления вероятности в схеме Бернулли согласно локальной формуле Муавра-Лапласа. Локальная формула Муавра-Лапласа. Функция Гаусса и её свойства. 16.Определение схемы Бернулли. Условия для приближенного вычисления вероятности в схеме Бернулли согласно интегральной формуле Муавра-Лапласа. Интегральная формула Муавра-Лапласа. Функция Лапласа и её свойства. 17.Определение схемы Бернулли. Отклонение относительной частоты от постоянной вероятности в независимых испытаниях. Основные задачи связанные с относительной частотой и вероятностью событий в независимых испытаниях. 18.Определение случайной величины. Закон распределения и функция распределения случайной величины. 19.Определение закон распределения дискретной случайной величины и её основное свойства. Привести простой примеры 19.Определение функции распределения случайной величины и её основные свойства. Привести простой пример. 20.Закон и функция распределения случайной величины и их взаимосвязь. 21Плотность распределения случайной величины и её основные свойства. Связь между функцией и плотностью распределения. 22.Функция и плотность распределения сложной случайной величины. 23.Математическое ожидание дискретной случайной величины и его основные свойства. 23.Математическое ожидание непрерывной случайной величины и его основные свойства. 24.Дисперсия дискретной случайной величины и её основные свойства. 24.Дисперсия непрерывной случайной величины и её основные свойства 24.Дисперсия непрерывной случайной величины и её основные свойства. 25.Ковариация и корреляция случайных величин. Основные свойства корреляции случайных величин. 26.Биноминальное распределение и его числовые характеристики. 27.Распределение Пуассона и его числовые характеристики. 28.Геометрическое распределение и его основные числовые характеристики. 29Равномерное распределение и его основные числовые характеристики. 30.Показательное распределение и его основные числовые характеристики. 31.Нормальное распределение и его основные числовые характеристики. Правило трёх сигм.
Тема: «Математическая статистика». 1. Предмет и задачи математической статистики. 2.Первичная обработка выборки: выборки; Вариационный и интервальный ряд. 3.Статистическая функция распределения. Полигон и гистограмма 4.Понятие оценки параметров генеральной совокупности. Основные свойства оценки. (точечные и доверительные оценки для средней и дисперсии генеральной совокупности) 5.Точечные оценки для средней и дисперсии генеральной совокупности. 6.Методы нахождения точечной оценки: метод моментов; метод максимального правдоподобия; метод наименьших квадратов. 7.Понятие интервального оценки.Доверительный интервал и доверительная вероятность. 8. Понятие о доверительных интервалах. Доверительный интервал для средней и дисперсии нормально распределенной генеральной совокупности . 9.Метод построения доверительного интервала для генеральной средней и генеральной доли по большим и малой выборки. 10.Доверительный интервал для генеральной дисперсии. 11. Статистическая гипотеза и общая схема ее проверки. Статистическая проверка гипотез и критерии согласия 12.Проверка гипотез о равенстве средних двух и более совокупностей. 13. Проверка гипотез о равенстве долей признака в двух и более совокупностей. 14.Сравнение дисперсий двух совокупностей. 15. Проверка гипотез о законе распределения. 1 6.Корреляционный и регрессионный анализ. 17.Уравнений парной регрессии. 18.Дисперсионный анализ. 13. Примерная тематика заданий для самостоятельной работы студентов В течение семестра студенты разбирают и решают задачи, указанныепреподавателем к каждому практическому занятию, разбирают и повторяют основные понятия и теоремы, рассмотренные на лекциях. Самостоятельная работа студентов предполагает знакомство с литературой по данной проблематике, подготовку проектов, докладов на студенческую научную конференцию. Контроль качества подготовки осуществляется путем проверки теоретических знаний и практических навыков путем 1) промежуточных самостоятельных работ студента (СРС), выполняемых, как правило, на практических занятиях и охватывающих материал отдельной темы; 2) проверки выполнения индивидуальных домашних заданий (ИДЗ) и проведении их защиты; 3) проведения коллоквиумов в устной форме или форме компьютерного тестирования; Примерные оценочные средства для текущего контроля успеваемости в виде «нулевого» варианта и промежуточной аттестации по итогам освоения дисциплины приведены ниже. Студент должен выполнить контрольные работы по следующим разделам. Контрольная работа №1 -Элементы векторной, линейной алгебры и аналитической геометрии. Контрольная работа №2 - Введение в математический анализ. Производная и ее приложения. Контрольная работа №3 - Неопределенный и определенный интегралы. Функции нескольких переменных. Дифференциальные уравнения. Контрольная работа №4- Кратные интегралы. Контрольная работа №5- Теория вероятностей. Математическая статистика. В течение семестра студент должен выполнить контрольные работы по варианту, номер которого совпадает с номером в списке журнала учета преподавателя. Номера задач самостоятельных работ приведены в табл. 1. Например, в самостоятельной работе № 1,студент имеющий номер 2 в списке журнала, выбирает задачи согласно варианту 2(см. табл. 1): 2, 12, 22, 32, 42, при этом номер варианта для всех самостоятельных работ не меняется. Таблица 1
САМОСТОЯТЕЛЬНАЯ РАБОТА (СРС) Типовые задачи к экзамену соответствуют заданиям самостоятельных, контрольных работ и индивидуальных заданий, выполняемых в течение семестра. Самостоятельная работа №1 Тема: «Элементы векторной, линейной алгебры и аналитической геометрии»
1 – 10. Даны координаты вершин пирамиды А1, А2, А3, А4. Найти: 1) угол между ребром А1А4 и гранью А1А2А3; 2) площадь грани А1А2А3; 3) объем пирамиды; 4) уравнение плоскости А1А2А3; 5) уравнения и длину высоты, опущенной из вершины А4 на грань А1А2А3 , а также координаты точки пересечения высоты с плоскостью А1А2А3. Сделать чертеж. 1. А1 (4; 2; 5), А2 (0; 7; 2), А3 (0; 2; 7), А4 (1; 5; 0) . 2. А1 (4; 4; 10), А2 (4; 10; 2), А3 (2; 8; 4), А4 (9; 6; 4) . 3. А1 (4; 6; 5), А2 (6; 9; 4), А3 (2; 10; 10), А4 (7; 5; 9) . 4. А1 (3; 5; 4), А2 (8; 7; 4), А3 (5; 10; 4), А4 (4; 7; 8) . 5. А1 (10; 6; 6), А2 (-2; 8; 2), А3 (6; 8; 9), А4 (7; 10; 3) 6. А1 (1; 8; 2), А2 (5; 2; 6), А3 (5; 7; 4), А4 (4; 10; 9) . 7. А1 (6; 6; 5), А2 (4; 9; 5), А3 (4; 6; 11), А4 (6; 9; 3) . 8. А1 (7; 2; 2), А2 (5; 7; 7), А3 (5; 3; 1), А4 (2; 3; 7) . 9. А1 (8; 6; 4), А2 (10; 5; 5), А3 (5; 6; 8), А4 (8; 10; 7) . 10. А1 (7; 7; 3), А2 (6; 5; 8), А3 (3; 5; 8), А4 (8; 4; 1) .
11. Прямые 2х+у-1 = 0 и 4х-у-11=0 являются сторонами треугольника, а точка Р(1; 2) – точкой пересечения третьей стороны с высотой, опущенной на нее. Составить уравнение третьей стороны. Сделать чертеж. 12. Прямая 5х-3у+4 = 0 является одной из сторон треугольника, а прямые 4х-3у+2 = 0 и 7х+2у-13 = 0 его высотами. Составить уравнения двух других сторон треугольника. Сделать чертеж. 13. Точки А (3; -1) и В (4; 0) являются вершинами треугольника, а точка D (2; 1) - точкой пересечения его медиан. Составить уравнение высоты, опущенной из третьей стороны. Сделать чертеж. 14. Прямые 3х-4у+17 = 0 и 4х-у-12 = 0 являются сторонами параллелограмма, а точка Р (2; 7) – точкой пересечения его диагоналей. Составить уравнения двух других сторон параллелограмма. Сделать чертеж. 15. Прямые х-2у+10 = 0 и 7х+у-5 = 0 являются сторонами треугольника, а точка D (1; 3) – точкой пересечения его медиан. Составить уравнение третьей стороны. Сделать чертеж. 16. Прямые 5х-3у+14 = 0 и 5х-3у-20 = 0 являются сторонами ромба, а прямая х-4у-4 = 0 – его диагональю. Составить уравнения двух других сторон ромба. Сделать чертеж. 17. На прямой 4х+3у-6=0 найти точку, равноудаленную от точек А (1; 2) и В (-1; -4). Сделать чертеж. 18. Найти координаты точки, симметричной точке А (5; 2) относительно прямой х+3у-1=0. Сделать чертеж. 19. Прямые х-3у+3=0 и 3х+5у+9=0 являются сторонами параллелограмма, а точка Р (34 –1) – точкой пересечения его диагоналей. Составить уравнения двух других сторон параллелограмма. Сделать чертеж. 20. Точки А (4; 5) и С (2; -1) являются двумя противоположными вершинами ромба, а прямая х-у+1=0 – одной из его сторон. Составить уравнения остальных сторон ромба. Сделать чертеж.
21–30. Даны векторы
31–40. Дана матрица А. Найти матрицу А-1 обратную данной. Сделать проверку, вычислив произведение А . А-1 .
41 – 50. Применяя метод исключения неизвестных (метод Гаусса), решить систему линейных уравнений.
Самостоятельная работа №2 Тема; «Введение в математический анализ. Производная и ее приложения»
1 – 10. Найти пределы функций, не пользуясь правилом Лопиталя.
2.
в)
3. а) в)
4.
в)
5. а) в) 6. а) в) 7. а) в) 8. а) в) 9. а) б) 10. а) в)
11 – 20. Задана функция y=f(x). Установить, является ли данная функция непрерывной. В случае разрыва функции в некоторой точке найти ее пределы слева и справа, классифицировать характер разрыва. Построить схематично график функции.
17. 18. 19. 20.
21 – 30. Найти производные 21. б)
22 в) 23. а) в) x = sin23t, y = cos23t .
24. в) x = t4 + 2t, y = t2 + 5t . 25. в) x = t – ln sint, y = t + ln cost . 26. a) в) x = tg t , 27. a) в) x = t2 – t3 , y = 2t3 . 28. a) y = lncos2x – lnsin2x ; б) в) x = cos3t , y = sin3t .
29. a) в) x = 3sint, y = 3cos2t . 30. в) x = 2t – t2 , y = 2t3 .
31 – 40. Найти дифференциал функций. 31. 32. 33 34. а)
35. 36.a) 37. a) 38. a) y = lncos2x – lnsin2x ; б)
39. a)
40. а)
41 – 51. Методами дифференциального исчисления: a) исследовать функцию y = f(x) и по результатам исследования построить ее график; 41. а) 42. а) 43. а) 44. а) 45. а) 46. а) 47. а) 48. а) 49. а) 50. а)
Самостоятельная работа №3 Тема: «Неопределенный и определенный интегралы. Дифференциальные уравнения. Функции нескольких переменных»
1 – 10. Найти неопределенные интегралы. В случаях а), б) результат проверить дифференцированием.
1.
2.
3.
4. а) в)
5. а) в)
6. а) в) 7. а) в) 8. а) в)
9. а) в) 10. а) в)
11-20. Вычислить определенные интегралы. 11. 13. 15. 17. 19.
21 - 31. Найти решения дифференциальных уравнений первого порядка, удовлетворяющие указанным начальным условиям. Сделать проверку. 21 а) б) в) y ¢¢ - 3y¢ - 4y = e-x, y(0) = 0, y¢ (0) = -1.
22. а) xy¢ + xey/x – y = 0, y(1) = 1 . б) в) y¢¢ - 6y¢ + 9y = x+1, y(0) = 1, y¢ (0) = 0 . 23. а) 20xdx – 3ydy = 3x2ydy – 5xy2dx, y(1) = 1 . б) в) y¢¢ + 9y¢ = x-2 , y(0) = -2, y¢ (0) = 1 . 24. а) б) в) y¢¢ - 2y¢ + 10y = sin3x, y(0) =1, y¢ (0) = 1
25. а) 3(x 2 y + y)dy + б) в) y¢¢ + y¢ - 6y = 2e-3x, y(0) = 0, y¢ (0) = 2 .
26. а) б) в) y¢¢ + 4y = x2, y(0) = -1, y¢ (0) = 0 . 27. а) б) в) y¢¢ - 3y¢ = cos 2x, y(0) = 3, y¢ (0) = 1 .
28. а) б) в) y¢¢- 4y¢ + 4y = 2sin3x, y(0) =0, y¢ (0) = -1.
29. а) б) в) y¢¢ + 4y¢ + 5y = 4ex, y(0) = 2, y¢ (0) = 0 .
30. а) б) в) y¢¢ + 4y¢ = cos x, y(0) = -2, y¢ (0) = -1 .
31 – 40. Найти наибольшее и наименьшее значения функции z = f (x; y) в ограниченной замкнутой области D. Область D изобразить на чертеже. 31. z = x2 – y2 + 3xy + 7 ; D : -2 £ x £ 2, -2 £ y £ 2 . 32. z = x2 + 2y2 – 1 ; D : x ³ -2, y ³ -2, x + y £ 4 . 33. z = 3 – x2 – xy – y2 ; D : x £ 1, y ³ -1, x +1 ³ y . 34. z = x2 + y2 + x – y ; D : x ³ 1, y ³ -1, x + y £ 2 . 35. z = x2 +2xy +2y2 ; D : -1 £ x £ 1, -1 £ y £ 3 . 36. z = 3x2 – 3xy +y2 + 1 ; D : x ³ -1, y ³ -1, x + y £ 1 . 37. z = 5 + 2xy – x2 ; D : -1 £ y £ 4 – x2 . 38. z = x2 – 2xy – y2 + x ; D : x £ 0, y £ 1, x + y + 2 ³ 0 . 39. z = x2 – xy – 2 ; D : 4x2 – 4 £ y £ 1 . 40. z = x2 + xy + 3y2 ; D : -1 £ x £ 1, -1 £ y £ 1 . 41 – 50. Даны: функция трех переменных u = f (x, y, z) , точка M0 (x0; y0; z0) и вектор 41. 42. u = ln|3x2 – 2y + z|; M0 (1; 1; 0) ; 43. 44. 45. 46. u = ln|10 – x2 – y2 – z2| ; M0 (2; 2; 1) ; 47. 48. u = x2y2 + x2z2 + y2z2 ; M0 (-1; 2; 1) ; 49. 50. u = ln|12 – x2 – y2 + z| ; M0 (1; 1; -5) ;
Самостоятельная работа №4 |
|
 и
и  .
. .
. .
. -критерий Пирсона.
-критерий Пирсона. в некотором базисе. Показать, что векторы
в некотором базисе. Показать, что векторы  образуют базис, а также найти координаты вектора
образуют базис, а также найти координаты вектора  в этом базисе. Систему линейных уравнений решить по формулам Крамера.
в этом базисе. Систему линейных уравнений решить по формулам Крамера.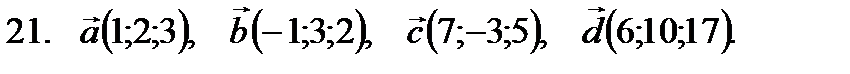

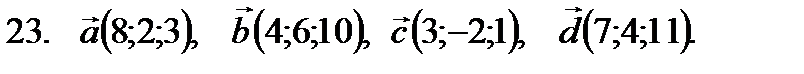
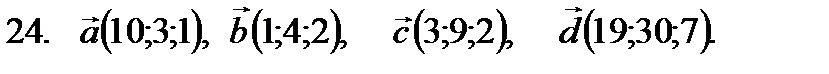

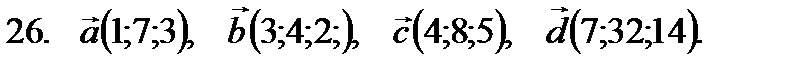
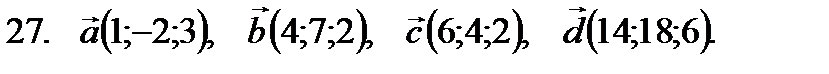
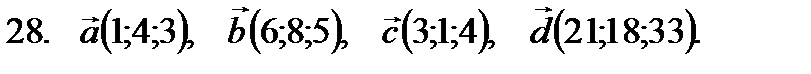
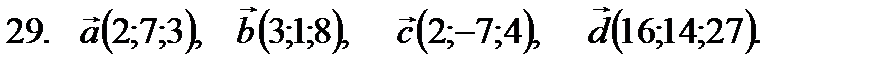
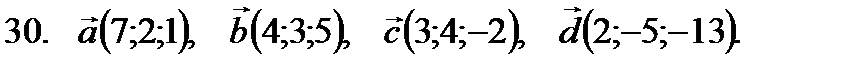



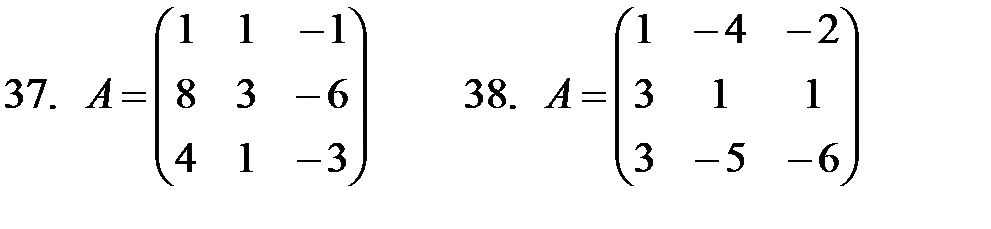
 .
.
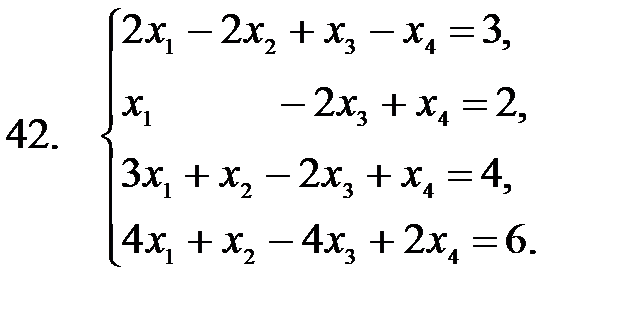

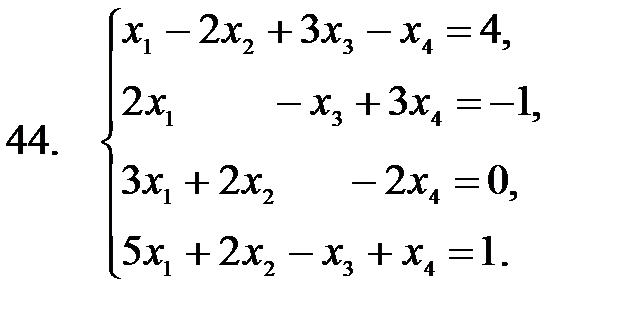

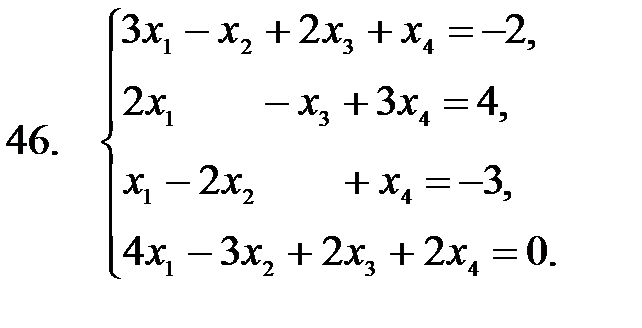

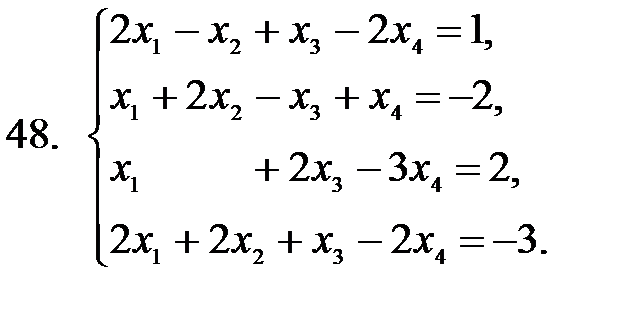
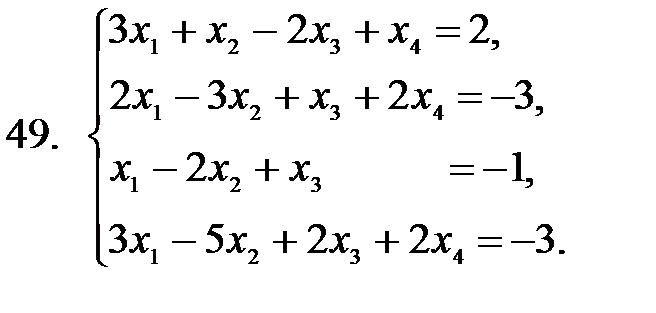
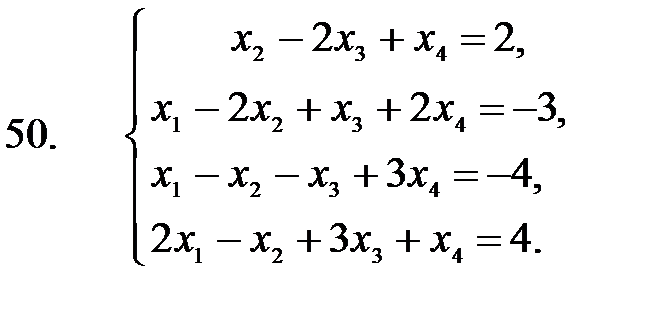
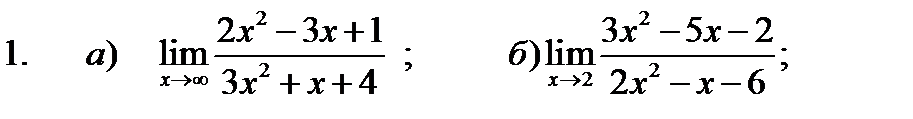



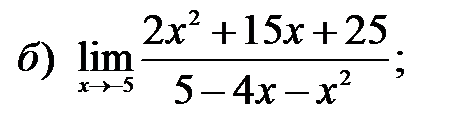
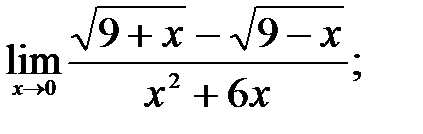 г)
г) 
 б)
б) 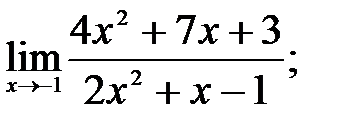
 г)
г) 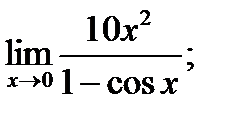

 г)
г) 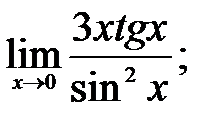
 б)
б) 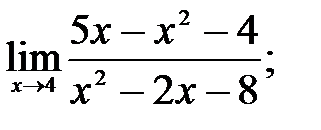
 г)
г) 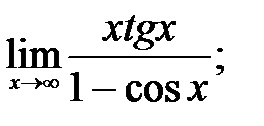
 б)
б) 
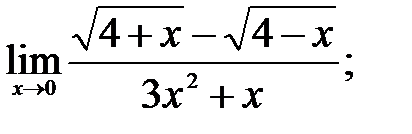 г)
г) 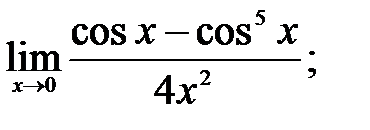
 б)
б) 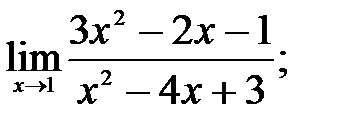
 г)
г) 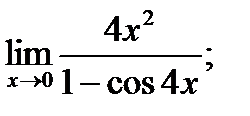
 ; б)
; б) 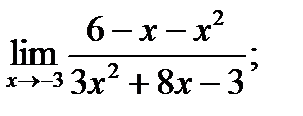
 г)
г) 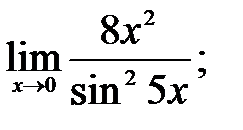
 б)
б) 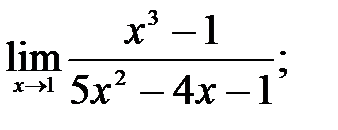
 г)
г) 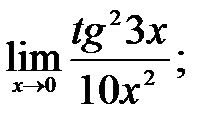
 б)
б) 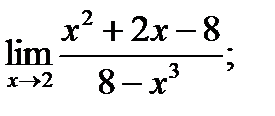
 г)
г) 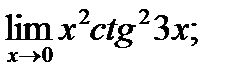
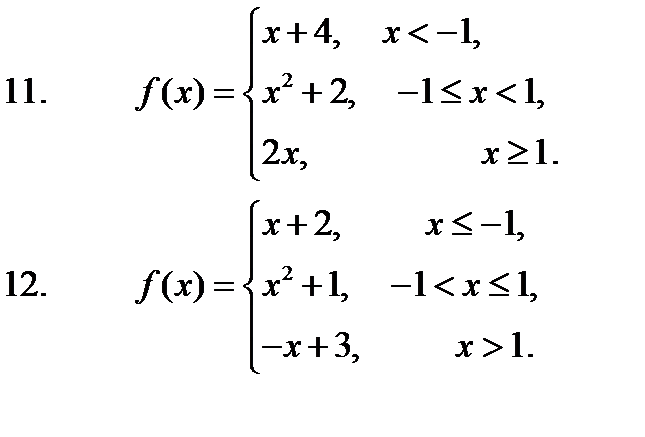

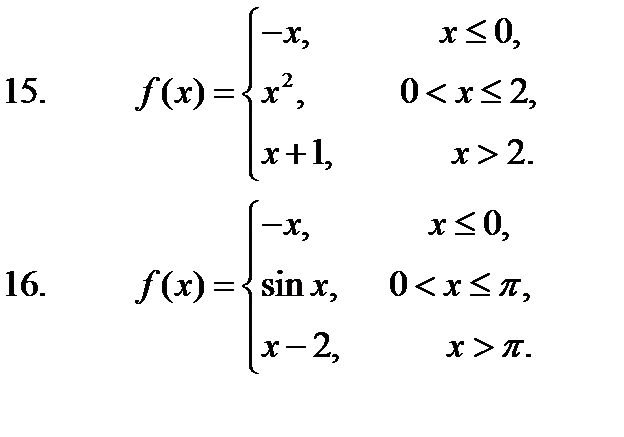
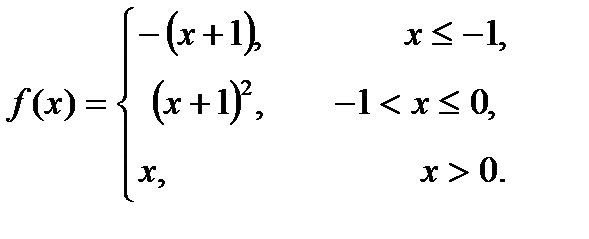
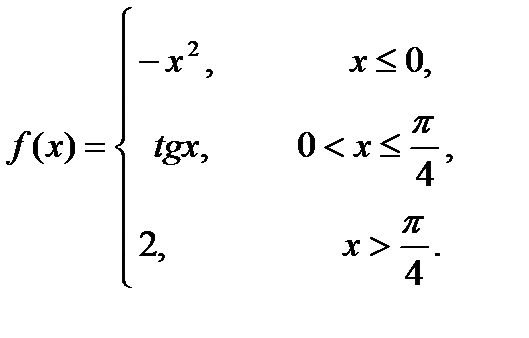
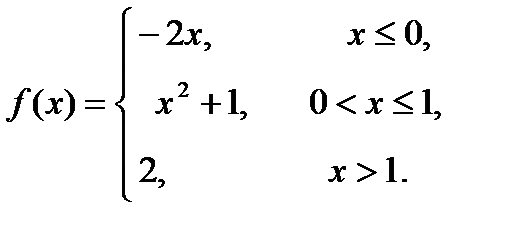
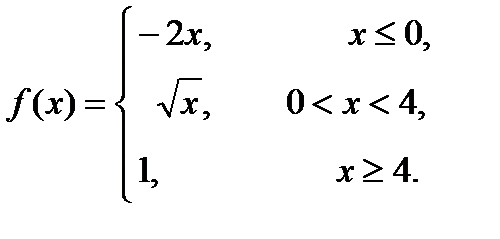
 следующих функций.
следующих функций. ;
;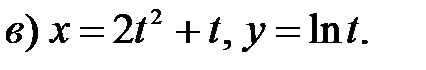
 б)
б)  ;
;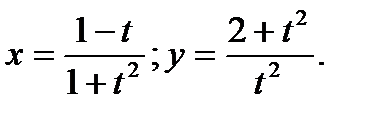
 б)
б)  ;
;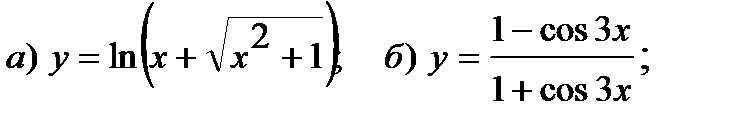
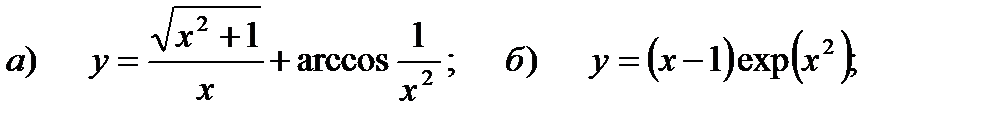
 б) y = exp(cos3x) .
б) y = exp(cos3x) .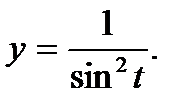
 б) y = 3x exp(-x-2) ;
б) y = 3x exp(-x-2) ;
 б)
б) 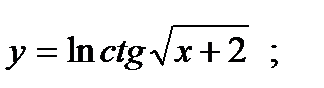

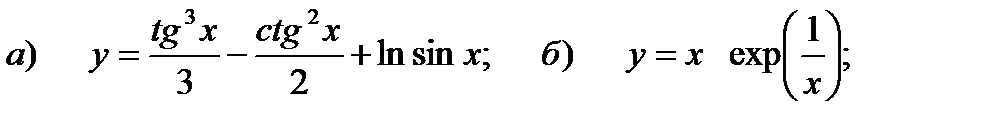
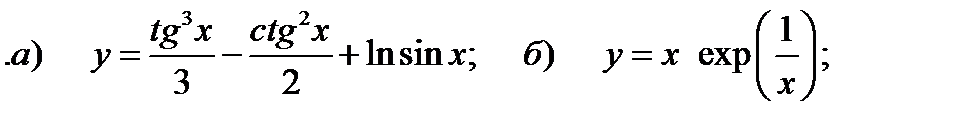
 б) [-3; 3 ] .
б) [-3; 3 ] . б) [-1; 1 ] .
б) [-1; 1 ] . б) [-2; 2 ] .
б) [-2; 2 ] . б) [-2; 2 ] .
б) [-2; 2 ] . б) [ 1; 4 ] .
б) [ 1; 4 ] . б) [ 0; 1 ] .
б) [ 0; 1 ] . б) [ 1; 9 ] .
б) [ 1; 9 ] . б) [-1; 1 ] .
б) [-1; 1 ] . б) [-2; 2 ] .
б) [-2; 2 ] . б) [-2; 2 ] .
б) [-2; 2 ] .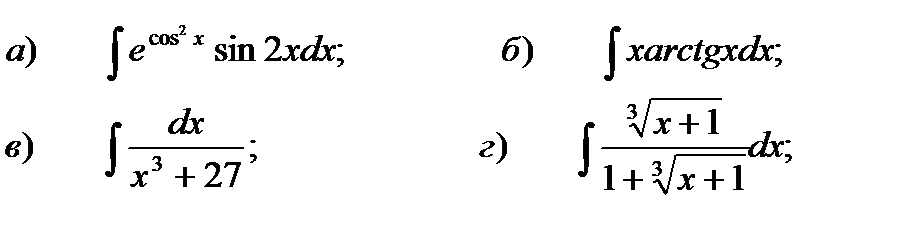
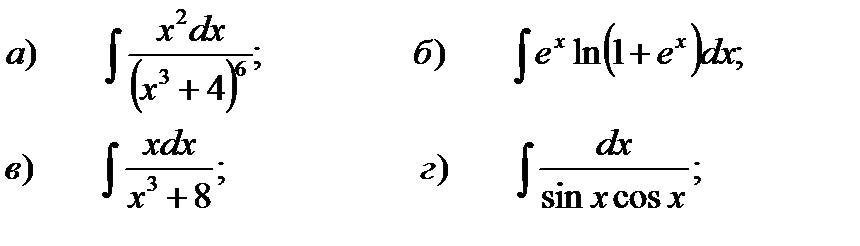
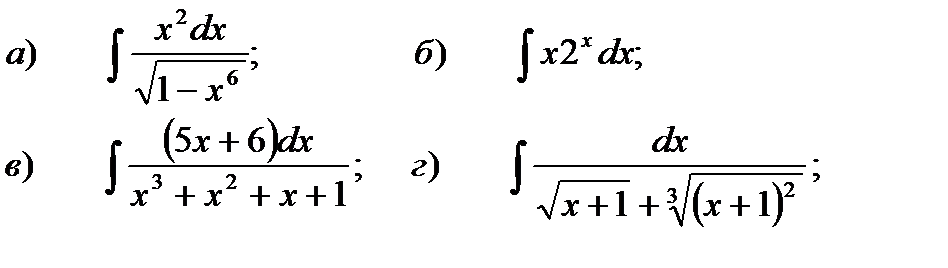
 б)
б) 
 г)
г) 
 б)
б) 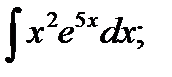
 г)
г) 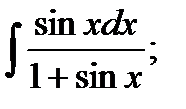
 б)
б) 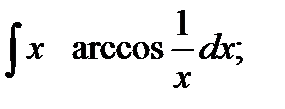
 г)
г) 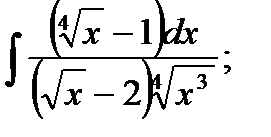
 б)
б) 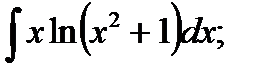
 г)
г) 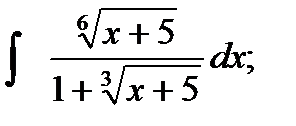
 б)
б) 
 г)
г) 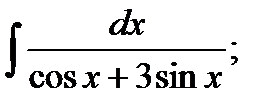
 б)
б) 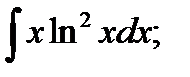
 г)
г) 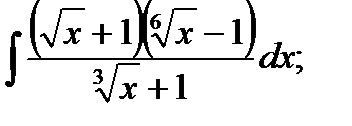
 б)
б) 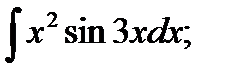
 г)
г) 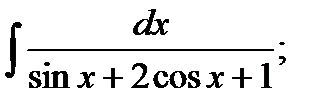
 12.
12. 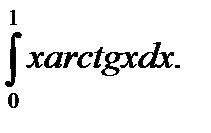
 14.
14. 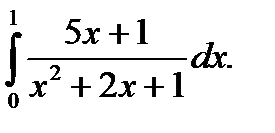
 16.
16. 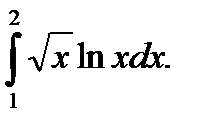
 18.
18. 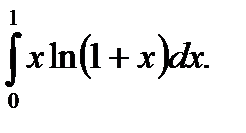
 20.
20. 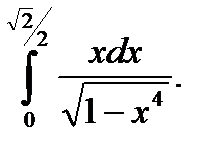
 у(1) = 0 ,
у(1) = 0 , .
. .
. .
. = y ln (y/x), y(1) = e .
= y ln (y/x), y(1) = e . .
. = 0, y(0) = 0 .
= 0, y(0) = 0 . .
. + б) y = x + 1, y(1) = 0 .
+ б) y = x + 1, y(1) = 0 . .
. cosx = (y + 1)sinx, y(0) = 0 .
cosx = (y + 1)sinx, y(0) = 0 . .
. – y =
– y =  , y(1) = 0 .
, y(1) = 0 . .
. – y/x = x2, y(1) = 0 .
– y/x = x2, y(1) = 0 . .
. , y(0) = 0 .
, y(0) = 0 . .
. (а1, а2,, а3) . Найти: 1) grad u в точке М0; 2) производную в точке М0 по направлению вектора
(а1, а2,, а3) . Найти: 1) grad u в точке М0; 2) производную в точке М0 по направлению вектора  M0 (1; -2; 1) ;
M0 (1; -2; 1) ;  (-1; 2; 2) .
(-1; 2; 2) . M0 (1; 1; 2) ;
M0 (1; 1; 2) ;  M0 (1; 2; 2) ;
M0 (1; 2; 2) ;  M0 (2; 2; 1) ;
M0 (2; 2; 1) ;  M0 (3; 4; 0) ;
M0 (3; 4; 0) ;  M0 (3; 4; 0) ;
M0 (3; 4; 0) ;