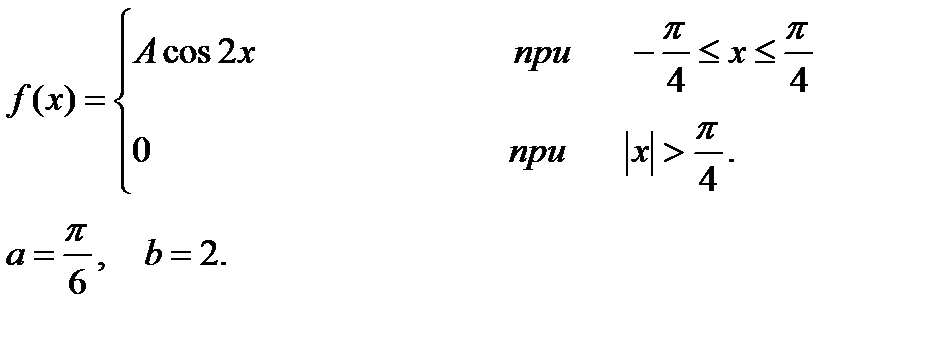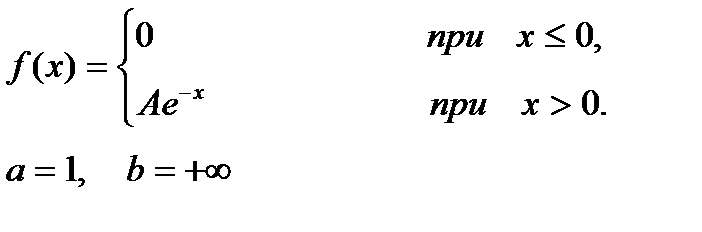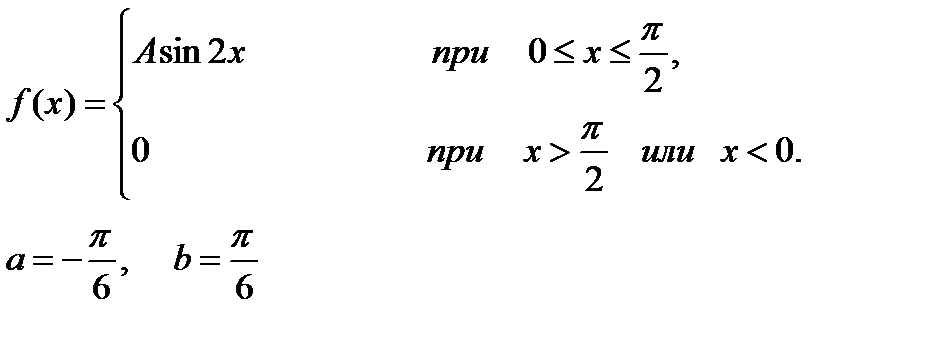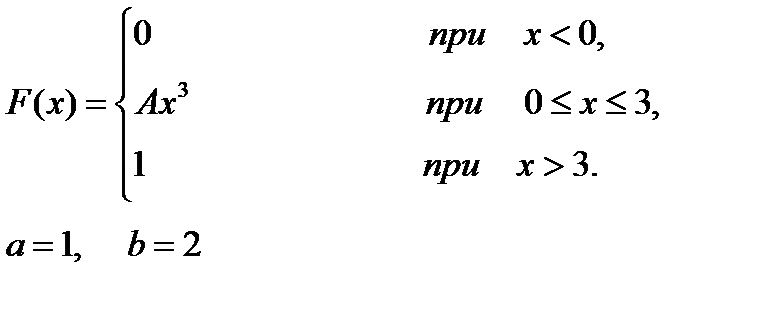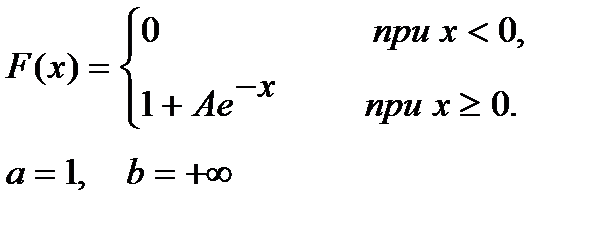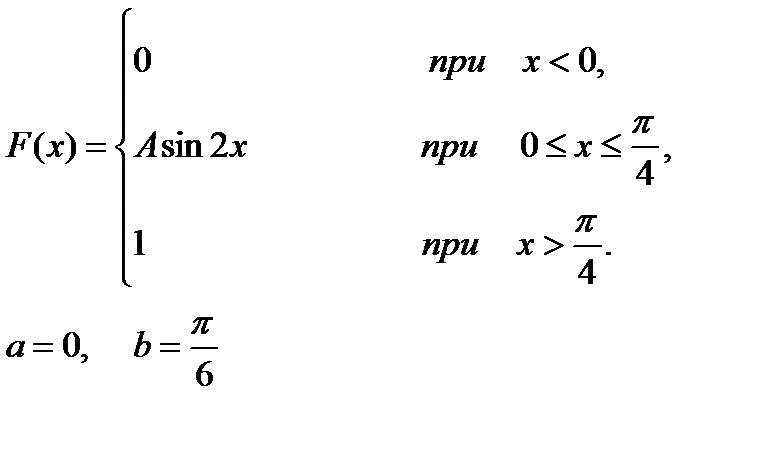|
|
Тема: «Кратные интегралы. Криволинейные и поверхностные интегралы»
1– 10. Вычислить двойной интеграл по области D. Область интегрирования D изобразить на чертеже. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
11-20. Изменить порядок интегрирования. 11 13. 15. 17. 19. 21-30. Вычислить тройные интегралы: 21. 22 23. 24. 25. 26. 27. 28. 29. 30.
31-40. Вычислить криволинейный интеграл. Сделать чертеж дуги кривой L.
31. 32. 33. 34. 35. 36. 37. 38. 39. 40.
41-45.Вычислить поверхностные интегралы 1-го рода.
41. отсеченная плоскостями
42. отсеченная плоскостями 43. отсеченная плоскостями 44. отсеченная плоскостью 45. отсеченная плоскостью
46-50.С помощью формулы Остроградского вычислить поверхностные интегралы. 46. 47.
48.
49.
50.
Самостоятельная работа № 5 Тема: «Теория вероятностей. Математическая статистика»
1. В барабане револьвера шесть гнезд, из которых в четыре вложены патроны, а два пустые. Барабан приводится в движение, в результате чего против ствола оказывается одно из гнезд. После этого нажимают спусковой крючок. Если гнездо пустое, то выстрела не происходит. Найти вероятность того, что в результате двух опытов: а) выстрела не произойдет; б) произойдет два выстрела; в) произойдет хотя бы один выстрел. 2. В лифт девятиэтажного дома вошли три человека. Предположим, что каждый из них с равной вероятностью может выйти на любом из этажей, начиная со второго. Найти вероятность того, что все пассажиры выйдут на одном этаже; что все пассажиры выйдут на разных этажах. 3. Вероятность хотя бы одного попадания при двух выстрелах равна 0,84. Найти: а) наивероятнейшее число попаданий в серии из семи выстрелов и модальную вероятность; б) что вероятнее: три попадания при четырех выстрелах или шесть попаданий при восьми? 4. Стрелок А поражает мишень с вероятностью 0,6 , стрелок В – с вероятностью 0,5 и стрелок С – с вероятностью 0,4. Стрелки дали залп по мишени и две пули попали в цель. Что вероятнее: попал стрелок С в мишень или нет? 5. В ящике десять стандартных деталей и пять бракованных. Наугад извлекаются три детали. Каковы вероятности того, что среди них: а) одна бракованная; б) две бракованных; в) хотя бы одна стандартная? 6. Имеются две партии однородных деталей. Первая партия состоит из 12 деталей, из которых три бракованных. Вторая партия состоит из 15 деталей, из которых четыре бракованных. Из первой и из второй партии извлекают по две детали. Какова вероятность того, что среди них нет бракованных деталей? 7. В ящике 100 деталей. Из них 20 деталей изготовлены первым заводом, 80 – вторым. Первый завод производит 90% хороших деталей, второй – 80%. Найти вероятность того, что две извлеченные наудачу детали окажутся хорошими. 8. Из урны, содержащей три белых и два черных шара, переложены два вынутых наудачу шара в урну, содержащую четыре белых и четыре черных шара. Найти вероятность вынуть из второй урны белый шар. 9. В коробке лежат девять теннисных мячей, из которых шесть новых. Для первой игры взяли два мяча, которые после игры возвратили. Для второй игры также взяли два мяча, оказавшиеся новыми. Какова вероятность того, что для первой игры брали два старых мяча? 10.Для изделий некоторого производства вероятность удовлетворять стандарту равна 0,96. Предлагается упрощенная система испытаний, дающая положительный результат с вероятностью 0,98 для изделий, удовлетворяющих стандарту, а для изделий, которые не удовлетворяют стандарту, с вероятностью 0,05. Какая вероятность того, что изделие, выдержавшее испытание, удовлетворяет стандарту?
11-15. Задана непрерывная случайная величина Х своей плотностью распределения вероятностей f(x). Требуется: 1) определить коэффициент А; 2) найти функцию распределения F(x); 3) схематично построить графики функций f(x) и F(x); 4) вычислить математическое ожидание и дисперсию Х; 5) определить вероятность того, что Х примет значение из интервала
11.
12.
13.
14. 15.
16-20. Задана непрерывная случайная величина Х своей функцией распределения F(x) . Требуется: 1) определить коэффициент А; 2) найти плотность распределения вероятностей f(x) ; 3) схематично построить графики функций f(x) и F(x) ; 4) вычислить математическое ожидание и дисперсию Х ; 5) определить вероятность того, что Х примет значение из интервала
16.
17.
18.
19.
20.
21-30. Нормально распределенная случайная величина Х задана своими параметрами а (математическое ожидание) и s (среднеквадратическое отклонение). Требуется: а) написать плотность вероятности и схематически изобразить ее график; б) найти вероятность того, что Х примет значение из интервала (a; b); в) найти вероятность того, что Х отклонится (по модулю) от а не более, чем на d ; г) применяя правило “трех сигм” найти значения случайной величины Х.
21. а = 7, s = 2, a = 6, b = 10, d = 3 . 22. a = 6, s = 1, a = 4, b = 7, d = 1 . 23. a = 5, s = 3, a = 1, b = 6, d = 2 . 24. a = 4, s = 2, a = 5, b = 6, d = 4 . 25. a = 3, s = 1, a = 4, b = 6, d = 2 . 26. a = 2, s = 1, a = 1, b = 3, d = 2 . 27. a = 10, s = 4, a = 5, b = 12, d = 2 . 28. a = 9, s = 5, a = 4, b = 12, d = 2,5 . 29. a = 8, s = 2, a = 5, b = 10, d = 3 . 30. a = 7, s = 3, a = 4, b = 8, d = 2 .
31-40. Данные наблюдений над случайной двумерной величиной (Х, У) представлены в корреляционной таблице. Методом наименьших квадратов найти выборочное уравнение прямой регрессии У на Х. 31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41-50. Известно эмпирическое распределение выборки объема n случайной величины Х. Проверить гипотезу о распределении по закону Пуассона генеральной совокупности этой величины. Использовать критерий согласия Пирсона (хи-квадрат) при уровне значимости α = 0,05.
Контрольной работы № 1 по темам: «Линейная алгебра и аналитическая геометрия ». |
|
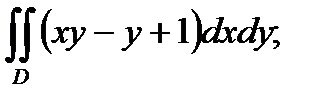 D : y = x2 , y = 2 – x2 .
D : y = x2 , y = 2 – x2 . D : x = 1 , y = x2 , y = 0 .
D : x = 1 , y = x2 , y = 0 . D : y = x , y = x3 , x ³ 0 .
D : y = x , y = x3 , x ³ 0 . D : y = x2 , y =
D : y = x2 , y =  .
. D : x = 1 , y =
D : x = 1 , y =  D : x = 1 , y = x2 , y = 0 .
D : x = 1 , y = x2 , y = 0 . D : y = x2 , y =
D : y = x2 , y =  D : x = 1 , y =
D : x = 1 , y = 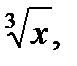 y = -x3 .
y = -x3 . D : y = x , y =
D : y = x , y =  D : x = 1 , y = x2 , y = -
D : x = 1 , y = x2 , y = -  х
х 12.
12. 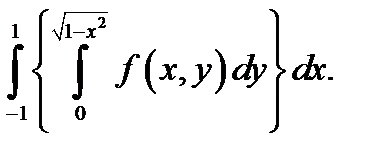
 14.
14. 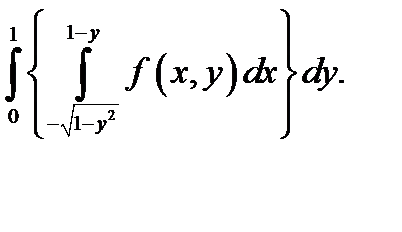
 16.
16. 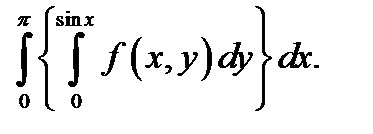
 18.
18. 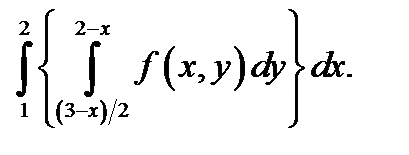
 20
20 
 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. , где L – отрезок прямой от точки (1; 0) до точки (0; -1).
, где L – отрезок прямой от точки (1; 0) до точки (0; -1). , где L – отрезок прямой от точки
, где L – отрезок прямой от точки  .
. , где L – дуга кривой y = ln x от точки (1; 0) до точки (е; 1).
, где L – дуга кривой y = ln x от точки (1; 0) до точки (е; 1). , где L – дуга кривой y = x2 от точки (1; 1) до точки (2; 4) .
, где L – дуга кривой y = x2 от точки (1; 1) до точки (2; 4) . , где L – верхняя половина окружности
, где L – верхняя половина окружности  , где L – дуга кривой y = x2 от точки
, где L – дуга кривой y = x2 от точки  , где L – первая четверть окружности
, где L – первая четверть окружности  , где L – отрезок прямой от точки (1; 2) до точки (2; 4) .
, где L – отрезок прямой от точки (1; 2) до точки (2; 4) . , где L – дуга кривой y = x2 от точки
, где L – дуга кривой y = x2 от точки  , где L – верхняя половина эллипса
, где L – верхняя половина эллипса  S-часть цилиндрической поверхности
S-часть цилиндрической поверхности 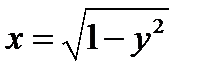 ,
,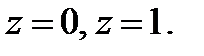
 S-часть поверхности
S-часть поверхности  ,
,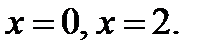
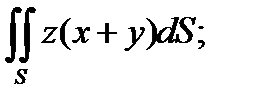 S-часть поверхности
S-часть поверхности  ,
,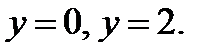
 S-часть поверхности
S-часть поверхности  ,
,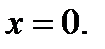
 S-часть поверхности
S-часть поверхности 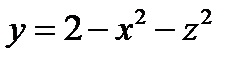 ,
,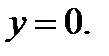
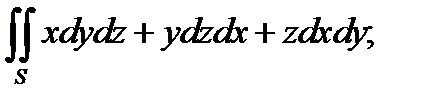 S-внешняя сторона пирамиды, ограниченная плоскостями
S-внешняя сторона пирамиды, ограниченная плоскостями 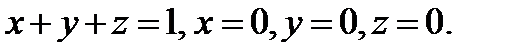
 S-внешняя сторона границы куба
S-внешняя сторона границы куба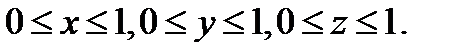
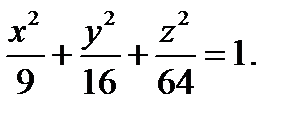
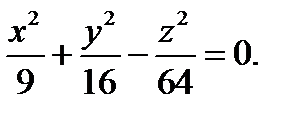
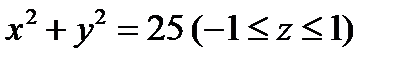 .
.