|
|
Трехфазная цепь, соединенная треугольником. Симметричная нагрузка.
Соединение обмоток генератора или фаз приемника, при котором начало одной фазы соединяется с концом другой, образуя замкнутый контур, называется соединением треугольником (
Начало фазы "А" источника питания соединяют с концом фазы "В" и точку соединения обозначают "А". Далее соединяют точки "В" и "Z" (точка "В") и точки "С" и "X" (точка "С"). Направления ЭДС приняты как и при рассмотрении схемы соединения звездой. Подобным образом соединяют треугольником и фазы приемника, сопротивления которых обозначены двумя индексами, соответствующими началу и концу фазы. По фазам приемника протекают фазные токи Поскольку каждая фаза нагрузки включена между линейными проводами, то линейное напряжение равно фазному напряжению:
Комплексные токи в фазах нагрузки могут быть определены по закону Ома:
где
Комплексные токи в линейных проводах связаны с фазными токами первым законом Кирхгофа:
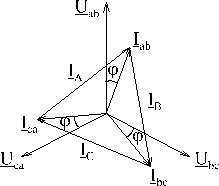
Итак, линейные токи при соединении треугольником равны векторной разности фазных токов тех фаз, которые соединены с данным линейным проводом. Отсюда следует, что векторная сумма линейных токов равна нулю:
Если нагрузка симметрична, то
и из полученных соотношений следует, что фазные токи нагрузки и линейные токи одинаковы:
а их векторы образуют симметричные системы.
Трехфазная цепь, соединенная треугольником при несимметричной Нагрузке.
В случае обрыва линейного провода А-а при соединении треугольником фазы нагрузки Согласно второму закону Кирхгофа
но поскольку
то
Напряжения на фазах
Рассматривая
Линейные токи определяются из уравнений первого закона Кирхгофа для узлов "с" и "b", но теперь
т.е. векторы фазе и по величине. Напряжение в месте обрыва определяется таким образом:
При несимметричной нагрузке отношение В случае обрыва фазы
при этом режимы работы остальных фаз не нарушаются, изменяются лишь линейные токи Соотношения между токами с учетом
Напряжение в месте обрыва равно линейному напряжению
Мощность трехфазной цепи.
Каждую фазу нагрузки в трехфазной цепи можно рассматривать как цепь однофазного переменного тока. Соотношения для мгновенной, активной, реактивной, полной и комплексной мощностей ранее были получены. Мгновенные мощности фаз можно определить согласно выражению:
Суммарная мгновенная мощность будет равна
Тогда получим
где Реактивная и полная мощности определяются так:
Через линейные токи и напряжения мощности могут быть определены:
При несимметричной нагрузке суммарные мощности определяются как алгебраические суммы мощностей отдельных фаз. Активная мощность трехфазного приемника равна сумме активных мощностей фаз и аналогично для реактивной. Полная мощность трехфазной цепи будет равна:
Тема 6. Переходные процессы
Основные понятия и принципы анализа переходных процессов.
Процессы в электрических цепях постоянного и переменного тока в установившемся состоянии были рассмотрены в предшествующих лекциях. Эти установившиеся режимы характеризуются тем, что токи в ветвях и напряжения на участках цепи или остаются неизменными или изменяются по одному и тому же закону, например: при постоянном напряжении при синусоидальном напряжении
Эти токи и напряжения называются установившимися токами и напряжениями. Любое изменение состояния электрической цепи (включение, отключение, изменение параметров цепи и т.д.) называется коммутацией. Будем считать, что процесс коммутации осуществляется мгновенно. Энергетическое же состояние цепи не может измениться мгновенно. Пример:
Если предположить, что ток в цепи изменяется мгновенно от
Но любая самоиндукция препятствует изменению тока в цепи. Поэтому предположение о мгновенном изменении тока в цепи неверно. Только в идеальном случае, когда Первый закон коммутации. Ток в цепи с катушкой индуктивности не может измениться скачком. Второй закон коммутации. Напряжение на зажимах конденсатора или другого емкостного элемента не может измениться скачком. Индуктивные и емкостные элементы являются инерционными, вследствие чего для изменения энергетического состояния электрической цепи требуется некоторый промежуток времени, в течение которого происходит процесс, который зависит от параметров цепи. Т.е. переход в установившийся режим, для которого соответствует строго определенное энергетическое состояние, например, для конденсатора определенное значение энергии электрического поля В этот промежуток времени (несколько секунд и доли секунды), токи и напряжения на отдельных участках цепи могут достигать больших значений иногда опасных для электроустановок. Поэтому необходимо уметь рассчитывать токи и напряжения переходных процессов и на основании полученных данных разрабатывать меры защиты электрической цепи. Переходный процесс можно описать дифференциальным уравнением. Режим линейных электрических цепей с постоянными параметрами
Общее (полное) решение дифференциального уравнения запишем в виде
где
Ток Ток Напряжение на элементах цепи
|
|
 ) . Таким образом, нагрузка включается между линейными проводами.
) . Таким образом, нагрузка включается между линейными проводами.
 . Условно положительное направление фазных токов приемника принято от точки первого индекса к точке второго индекса. Условно положительное направление фазных напряжений
. Условно положительное направление фазных токов приемника принято от точки первого индекса к точке второго индекса. Условно положительное направление фазных напряжений  совпадает с положительным направлением фазных токов. Условное положительное направление линейных токов
совпадает с положительным направлением фазных токов. Условное положительное направление линейных токов  принято от источника питания к приемнику.
принято от источника питания к приемнику.
 ;
;  ;
; 
 ;
;  ;
;  .
. ;
;  ;
;  .
. .
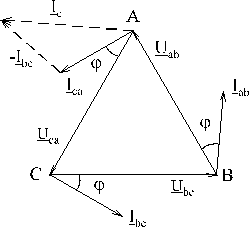
Система линейных-фазных напряжений
.
Система линейных-фазных напряжений  при соединении треугольником образует такой же замкнутый треугольник, как и при соединении звездой.
при соединении треугольником образует такой же замкнутый треугольник, как и при соединении звездой.
 ,
, ;
;  ,
,
 .
.
 ,
и симметрия векторных систем токов
нарушается. Но в любом случае система векторов фазных напряжений остается жесткой, а также всегда выполняется соотношение между линейными токами:
,
и симметрия векторных систем токов
нарушается. Но в любом случае система векторов фазных напряжений остается жесткой, а также всегда выполняется соотношение между линейными токами:

 и
и  оказываются соединенными последовательно, их можно рассматривать как одно общее сопротивление
оказываются соединенными последовательно, их можно рассматривать как одно общее сопротивление 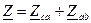 , которое, как и сопротивление фазы
, которое, как и сопротивление фазы 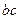 , находится под напряжением
, находится под напряжением  .
. ,
,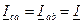 ;
;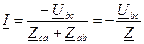
 ;
;  .
. как контур, получим соотношение:
как контур, получим соотношение:
 .
. и
и 

 и
и  совпадают по
совпадают по ;
; 
 является комплексным числом, значит, точка "а" находится вне отрезка
является комплексным числом, значит, точка "а" находится вне отрезка  ;
; 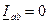
 и
и 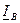 .
. имеют вид:
имеют вид: ;
; 

 .
. .
.

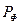 - активная мощность одной фазы, а
- активная мощность одной фазы, а  - суммарная активная мощность нагрузки. Получаем вывод: суммарная мгновенная мощность симметричной трехфазной цепи не изменяется во времени и равна суммарной активной мощности всей цепи.
- суммарная активная мощность нагрузки. Получаем вывод: суммарная мгновенная мощность симметричной трехфазной цепи не изменяется во времени и равна суммарной активной мощности всей цепи.
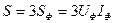
 ;
;
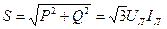
 ;
;

 , определяемый только сопротивлением цепи. При замыкании выключателя, т.е. при шунтировании резистора
, определяемый только сопротивлением цепи. При замыкании выключателя, т.е. при шунтировании резистора 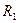 , установившийся ток в цепи
, установившийся ток в цепи  .
.

 до
до  то в индуктивной катушке в этот момент времени переменным током индуцируется ЭДС самоиндукции
то в индуктивной катушке в этот момент времени переменным током индуцируется ЭДС самоиндукции


 , можно рассматривать изменение тока как мгновенное.
, можно рассматривать изменение тока как мгновенное. и для индуктивной катушки энергии магнитного поля
и для индуктивной катушки энергии магнитного поля  , необходим некоторый промежуток времени
, необходим некоторый промежуток времени  .
. и
и  описывается линейным дифференциальным уравнением с постоянными коэффициентами. Так режим цепи синусоидального тока при последовательном соединении
описывается линейным дифференциальным уравнением с постоянными коэффициентами. Так режим цепи синусоидального тока при последовательном соединении  , описывается уравнением
, описывается уравнением

 - ток в переходном режиме,
- ток в переходном режиме, - частное решение данного неоднородного уравнения,
- частное решение данного неоднородного уравнения, - общее решение однородного дифференциального уравнения.
- общее решение однородного дифференциального уравнения. имеет тот же физический смысл, что и ток
имеет тот же физический смысл, что и ток