|
|
Релятивистский закон преобразования скорости.Выражение: Заметим, что эта формула применима только в том случае, если все три вектора — v, v' и V— направлены по одной прямой. В общем случае этот закон имеет более сложный вид. Однако при любой форме записи закона (6) его сущность заключается в выражении идеи предельности постоянной с: при любых относительных скоростях инерциальных систем отсчета V<c нельзя путем перехода от одной из них к другой изменить скорость частицы так, чтобы изменилась ее принадлежность к соответствующему классу частиц. Как и в случае классического закона, если направления скоростей v' и V противоположны, то в соотношении следует заменить V на -V, т. е. записать: Здесь v' и v — скорости данной частицы соответственно в инерциальных системах отсчета K' и K, V — относительная скорость этих систем отсчета . Координатное и собственное время. Из второго постулата специальной теории относительности следует, что частицы, движущиеся с абсолютной скоростью, не существуют в покое. Иными словами, их нельзя остановить, с ними нельзя связать систему отсчета. Напротив, для частиц, которые могут двигаться только со скоростью меньше абсолютной, имеет смысл состояние покоя. Систему отсчета, где такая частица покоится, назовем собственной системой отсчета частицы и обозначим К0. Под собственным временем частицы τ0 , понимается промежуток времени между любыми двумя событиями, относящимися непосредственно к частице, определяемый в ее собственной системе отсчета. Пусть в системе отсчета К равномерно со скоростью v движется частица А от метки а к метке b, где она находится соответственно в моменты времени t1 и t2 (по часам cистемы отсчета К). Итак, в системе отсчета К события (A, a) и (A, b) совершаются в разных пространственных точках — у меток а и b. Время, измеренное по часам в той системе отсчета К, относительно которой частица движется, назовем координатным временем τ промежуток времени между двумя событиями по этим часам (например, прохождение частицей А меток a и b) есть промежуток координатного времени (времени в системе отсчета K): В собственной системе отсчета К0 эти события происходят в одной пространственной точке, отмеченной самой частицей А. Промежуток времени между событиями (А, а) и (A, b) в системе отсчета К0 по определению равен собственному времени τ0 частицы для данных событий. Это время определяется по часам системы отсчета К0, покоящимся относительно этой частицы: На основании определения данного понятия, очевидно, что собственное время частицы абсолютно (инвариантно): Смысл данного утверждения заключается в следующем. Последовательность событий, связанных с частицей, и длительность процессов, состоящих из этих событии, не зависит по принципу относительности от выбора инерциальной системы отсчета, относительно которой частица покоится, — во всех таких системах отсчета последовательность событий и их длительность одинаковы. Образно говоря, «возраст» частицы (определяемый ее собственным временем) абсолютен, т.е. является инвариантом — величиной, независимой от выбора инерциальной системы отсчета. За счет изменения системы отсчета частица не может ни «состариться», ни «помолодеть». Относительность одновременности. Постулат специальной теории относительности об абсолютной скорости сразу отвергает гипотезу об абсолютной одновременности разноместных событий, значит, и представление о едином для всех инерциальных систем отсчета абсолютном времени. Чтобы в этом убедиться, рассмотрим следующий мысленный опыт. Пусть система отсчета К' связана с достаточно длинным «ящиком», который движется относительно системы отсчета К со скоростью V. В центре «ящика» расположен источник частиц, движущихся с абсолютной скоростью с, например источник света. При «вспышке» источника излучается пара таких частиц: одна из них движется к метке а, другая к метке b. Ясно, что соударения частиц с этими метками в системе отсчета К' (внутри «ящика») будут одновременными событиями. Относительно системы отсчета К метки а и b движутся со скоростью V так, что одной частице метку b нужно догонять. а к другой частице метка а движется навстречу. Так как скорости частиц одинаковы и равны с в обеих системах отсчета, то соударение с меткой а левой частицы произойдет раньше соударения правой частицы с меткой b. Таким образом, те же события — соударения частиц с метками а и b — будут неодновременными в системе отсчета К. Замедление времени. Относительность одновременности разноместных событий означает отсутствие абсолютного времени для всех инерциальных систем отсчета. Согласно принципу относительности в любой инерциальной системе отсчета время течет совершенно так же, как и в каждой совокупности инерциальных систем отсчета. Однако единого для всех инерциальных систем отсчета абсолютного времени не существует. Связь между собственным и координатным временем. Ясно, что соотношение между величинами τ и τ 0 зависит от скорости v движения частицы. Различие этих величин будет тем значительнее. чем ближе скорость частицы к предельной скорости. Действительно, при v>>c речь идет уже о частице, движущейся с абсолютной скоростью. А у такой частицы нет собственного времени (τ0 = 0), ибо с ней нельзя связать систему отсчета, но есть координатное время ее движения относительно системы отсчета τ 0. При v Итак, связь собственного времени частицы и ее координатного времени (времени ее движения со скоростью v в заданной инерциальной системе отсчета) определяется соотношением: Согласно этой формуле τ>τ0, т. е. время движения частицы в какой-либо инерциальной системе отсчета со скоростью v<c от «старта» до «финиша», определяемое часами данной системы отсчета, больше собственного времени, соответствующего тем же событиям («старту» и «финишу») и измеряемого часами, связанными с самой частицей. Время в неподвижной системе отсчета и движущейся относительно нее течет с разной скоростью: Из выражения (2) следует, что неподвижный наблюдатель обнаруживает замедление хода движущихся часов по сравнению с точно такими же, но находящимися в покое часами. Поскольку замедление времение свойство самого времени, то замедляют свой ход не только движущиеся часы. при движении замедляются все физические процессы, в том числе и химические реакции в человеческом организме, поэтому течение жизни замедляется в соответствующее число раз. Прямые эксперименты по проверке релятивистского соотношения (1) были поставлены в 70-х годах группой американских физиков. В них были использованы атомные часы с точностью хода порядка 10-19 с. Одни часы оставались в лаборатории. а другие отправлялись в длительные путешествия на самолетах. На заключительном этапе опыта показания всех часов вновь сравнивались в лаборатории. Результаты экспериментов подтвердили теоретический прогноз теории относительности.
Контрольные вопросы: 1.Какие величины называют инвариантными, какие относительными? Приведите примеры инвариантных и относительных величин. 2.Сформулируйте классический закон сложения скоростей. 3.Какой величиной, инвариантной или относительной является ускорение? Докажите. 4.Сформулируйте принцип относительности Галилея. Разъясните его смысл. 5.Что изучает специальная теория относительности и классическая? 6.Сформулируйте первый и второй постулаты теории относительности и объясните их смысл. 7.Сформулируйте релятивистский закон сложения скоростей, укажите границы применяемости классического закона сложения скоростей. 8.Какое время называется собственным, какое координатным? 9.Дайте понятие относительности одновременности. 10Как выражается связь собственного времени и её координатного времени. Объясните смысл взаимосвязи. 11.Во сколько раз замедляется время в ракете при её движении относительно земли со скоростью v= 2,6*108м/с? 12.Экскалатор метрополитена поднимает неподвижно стоящего на нем пассажира в течение 1 мин. По неподвижному экскалатору пассажир поднимается за 3 мин. Сколько времени будет подниматься пассажир по движущемуся экскалатору? 13.Два поезда идут навстречу друг другу со скоростями v1=36км/ч, v2=54км/ч. Пассажир в первом поезде замечает, что второй поезд проходит мимо него в течение времени t= 6с. Какова длина второго поезда? 14.Катер, переправляясь через реку, движется перпендикулярно течению реки со скоростью 4м/с в системе отсчета, связанной с водой. На сколько метров будет снесён катер течением, если ширина реки 800м, а скорость течения 1м/с? 15.Сестра в возрасте 18 лет, улетая в космическое путешествие, оставляет на Земле 14-летнего брата. Вернувшись через 2 года (по своим часам) на землю, она встречает брата, ставшего её ровесником. С кокой скоростью путешествовала девушка? 16. Две ракеты движутся навстречу друг другу относительно Земли с одинаковой скоростью, равной 0,5с. Определить скорость сближения ракет: согласно классической механике; в соответствии с релятивистским законом сложения скоростей.
Тема: «Основы динамики» Первый закон Ньютона (закон инерции). Первый закон Ньютона постулирует существование особого класса систем отсчета. В этих системах отсчета материальная точка (тело), не подверженное внешним воздействиям (такое тело называется свободным), находится в покое или движется равномерно и прямолинейно. Если существует хотя бы одна инерциальная система отсчета, в которой свободные тела покоятся или движутся равномерно и прямолинейно, то существует и бесконечное множество таких систем. Действительно, если в одной инерциальной системе отсчета свободное тело движется с постоянной скоростью и, то в системе отсчета, движущейся с постоянной скоростью v0 относительно первой, это свободное тело будет также иметь постоянную скорость, равную v1 = v0 + v. Таким образом, из первого закона Ньютона следует, что может двигаться как при наличии, так и при отсутствии внешнего воздействия. Взаимодействие тел. Причиной изменения скорости движения тела всегда является его взаимодействие с другими телами. После выключения двигателя автомобиль постепенно замедляет свое движение и останавливается. Основная причина изменения скорости движения автомобиля — взаимодействие его колес с дорожным покрытием. Неподвижно лежащий на земле мяч никогда сам собой не приходит в движение. Скорость мяча изменяется только в результате действия на него других тел, например ноги футболиста. При взаимодействии двух тел всегда изменяются скорости и первого, и второго тела, т. е. оба тела приобретают ускорения. Модули ускорений двух взаимодействующих тел могут быть различными, но их отношение оказывается постоянным при любых взаимодействиях:
Инертность тел. Постоянство отношения модулей ускорений двух тел при любых их взаимодействиях показывает, что тела обладают каким-то свойством, от которого зависит их ускорение при взаимодействиях с другими телами. Ускорение тела равно отношению изменения его скорости к времени, за которое произошло это изменение: Чем меньше изменяется скорость тела при взаимодействии с другими телами, тем ближе его движение к равномерному прямолинейному движению по инерции. Такое тело называют более инертным. Свойством инертности обладают все тела. Оно состоит в том, что для изменения скорости тела при взаимодействии его с любыми другими телами требуется некоторое время. Масса тела. Свойство тела, от которого зависит его ускорение при взаимодействии с другими телами, называется инертностью. Количественной мерой инертности тела является масса тела. Чем большей массой обладает тело, тем меньшее ускорение оно получает при взаимодействии. Поэтому в физике принято, что отношение масс взаимодействующих тел равно обратному отношению модулей их ускорений: За единицу массы в Международной системе принята масса специального эталона, изготовленного из сплава платины и иридия. Масса этого эталона называется килограммом (кг). Массу mт любого тела можно найти, осуществив взаимодействие этого тела с эталоном массой mэт. По определению понятия массы отношение масс взаимодействующих тел равно обратному отношению модулей их ускорений (2). Измерив модули ускорений ат тела и аэт эталона, можно найти отношение массы тела т, к массе эталона. Сила и ускорение. В инерциальных системах отсчета любое изменение скорости тела происходит под действием других тел. Описывая действие одного тела на другое, мы часто говорим о слабом, сильном или очень сильном действии. Но значение слов «сильный удар», «слабый удар», например, при описании действия клюшки хоккеиста на шайбу совершенно неопределенно, пока нет количественной меры действия одного тела на другое. В физике для количественного выражения действия одного тела на другое вводится понятие «сила». Когда нужно знать ускорение только одного из двух взаимодействующих тел и можно не рассматривать второе тело, то влияние одного тела на другое, вызывающее возникновение ускорения, называют силой, действующей на тело. Взаимодействие тел может приводить к различным изменениям их скоростей как по модулю, так и по направлению. Поэтому сила характеризуется не только числом, но и направлением. Сила — величина векторная, ее обозначают буквой F. За направление вектора силы принимается направление вектора ускорения тела, на которое действует сила. В Международной системе единиц за единицу силы принимается сила, которая телу массой 1 кг сообщает ускорение 1 м/с2. Эта единица называется ньютоном (Н): 1Н = 1 кг м/с. Второй закон Ньютона. Связь между силой и ускорением тела устанавливается на основании опыта. Если подействовать на одно и то же тело разными силами, то опыт показывает, что ускорение тела прямо пропорционально силе: a ~ F при m = const.
F = ma (5). Из этого закона, получившего название второго закона Ньютона, следует, что для определения ускорения тела нужно знать действующую на него силу и массу тела: a = F/m. Сложение сил. При одновременном действии на одно тело нескольких сил, тело движется с ускорением, являющимся векторной суммой ускорений, которые возникли бы под действием каждой силы в отдельности. Действующие на тело силы, складываются по правилу сложения векторов. Векторная сумма всех действующих на тело сил называется равнодействующей. F= N+F1
Используя второй закон Ньютона, получаем равенство: Это выражение, называемое третьим законом Ньютона, показывает, что тела действуют друг на друга с силами, направленными вдоль одной прямой. Эти силы равны по модулю, противоположны по направлению. Однако они не могут уравновешивать друг друга, так как приложены к разным телам. Закон всемирного тяготения. В XVI в. астроном Тихо Браге, в течение многих лет наблюдавший планеты, смог с наибольшей возможной в то время точностью определить их координаты в различные моменты времени. Обрабатывая результаты наблюдений Тихо Браге, астроном Иоган Кеплер установил формы орбит — траекторий, по которым движутся планеты, и некоторые особенности движения планет по этим орбитам. Оказалось, что планеты движутся по орбитам, близким к круговым, и отношение куба радиуса орбиты любой планеты к квадрату периода ее обращения вокруг Солнца есть величина постоянная, одинаковая для всех планет Солнечной системы: Обобщив этот вывод на все тела в природе, Ньютон получил закон всемирного тяготения: все тела (материальные точки), независимо от их свойств, притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними: где коэффициент пропорциональности G, одинаковый для всех тел в природе, получил название гравитационной постоянной G = 6,6720*10-11 Н*м2*кг-2.
Сила тяжести. Движение тела под действием силы тяжести. Сила тяжести - гравитационная сила, действующая на тело: F=m*g (10), где g- ускорение свободного падения, ускорение, приобретаемое телом под действием гравитационной силы вблизи поверхности небесных тел.
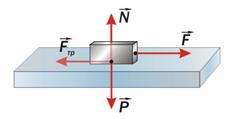
Отсюда первая космическая скорость равна Подставив в выражение (12) значения радиуса Земли и ускорения свободного падения у ее поверхности, получим, что первая космическая скорость для Земли v ~ 7,9 * 103 м/с = 7,9 км/с. Эта скорость примерно в 8 раз больше скорости пули. Первая космическая скорость для любого небесного тела также определяется выражением (12). Ускорение свободного падения на расстоянии R от центра небесного тела можно найти, воспользовавшись вторым законом Ньютона и законом всемирного тяготения: Вес тела. Весом тела называют силу, с которой тело действует на горизонтальную опору или подвес. Вес тела P, т. е. сила, с которой тело действует на опору, и сила упругости Fупр, с которой опора действует на тело, в соответствии с третьим законом Ньютона равны по модулю и противоположны по направлению: Если тело находится в покое на горизонтальной поверхности или равномерно движется и на него действуют только сила тяжести FT и сила упругости Fупр со стороны опоры, то из равенства нулю векторной суммы этих сил следует равенство:
Рассмотрим случай движения лифта, когда ускорение а направлено вертикально вниз. Если координатную ось ОУ направить вертикально вниз, то векторы P, g и a оказываются параллельными оси ОУ , а их проекции — положительными; тогда уравнение (19) примет вид Невесомость. Если тело вместе с опорой свободно падает, то а = g и из формулы (7) следует, что P= 0. Исчезновение веса при движении опоры с ускорением свободного падения называется невесомостью. Состояние невесомости наблюдается в самолете или космическом корабле при движении с ускорением свободного падения независимо от направления и значения модуля скорости их движения. За пределами земной атмосферы при выключении реактивных двигателей на космический корабль действует только сила всемирного тяготения. Под действием этой силы космический корабль и все тела, находящиеся в нем, движутся с одинаковым ускорением; поэтому в корабле наблюдается явление невесомости.
Сила трения покоя. Прикрепим к бруску крючок динамометра и попытаемся привести брусок в движение. Растяжение пружины динамометра показывает, что на брусок действует сила упругости, но тем не менее брусок остается неподвижным. Это значит, что при действии на брусок силы упругости в направлении, параллельном поверхности соприкосновения бруска со столом, возникает равная ей по модулю сила противоположного направления. Сила, возникающая на границе соприкосновения тел при отсутствии относительного движения тел, называется силой трения покоя. Сила трения покоя Fтр равна по модулю внешней силе F, направленной по касательной к поверхности соприкосновения тел, и противоположна ей по нaправлению : Сила трения скольжения. Прикрепим динамометр к бруску и заставим брусок двигаться равномерно по горизонтальной поверхности стола. Во время равномерного движения бруска динамометр показывает, что на брусок со стороны пружины действует постоянная сила упругости Fупр. При равномерном движении бруска равнодействующая всех сил, приложенных к нему, равна нулю. Следовательно, кроме силы упругости во время равномерного движения на брусок действует сила, равная по модулю силе упругости, но направленная в противоположную сторону. Эта сита называется силой трения скольжения. Вектор силы трения скольжения Fтр всегда направлен противоположно вектору скорости и движения тела относительно соприкасающегося с ним тела. Поэтому действие силы трения скольжения всегда приводит к уменьшению модуля относительной скорости тел. Силы трения возникают благодаря существованию сил взаимодействия между молекулами и атомами соприкасающихся тел.
Силу упругости N, возникающую в результате деформации опоры и действующую на тело, называют силой реакции опоры. По третьему закону Ньютона, сила давления и сила реакции опоры равны по модулю и противоположны по направлению: Опыт показывает, что модуль силы трения скольжения, как и модуль максимальной силы трения покоя, пропорционален модулю силы реакции опоры: Максимальное значение силы трения покоя примерно равно силе трения скольжения, приближенно равны также коэффициенты трения покоя и скольжения. Силы трения возникают и при качении тела. При одинаковой нагрузке сила трения качения значительно меньше силы трения скольжения. Поэтому для уменьшения сил трения в технике применяются колеса, шариковые и роликовые подшипники.
Контрольные вопросы и задания: 1.При каких условиях скорость тела остается неизменной? Сформулируйте закон инерции (первый закон Ньютона)? 2. Что такое инертность? Какая физическая величина является мерой инертности? 3.Какая физическая величина характеризует отсутствие или наличие внешнего воздействия? Дайте определение силы и назовите единицы силы. 4.Сформулируйте второй закон Ньютона. 5.Сформулируйте третий закон Ньютона. 6.В чем отличие гравитационного притяжения от сил упругости и трения? 7.Сформулируйте закон всемирного тяготения. 8.Что такое сила тяжести? Дайте определение ускорения свободного падения. 9.Дайте понятие первой космической скорости, чему она ровна? 10.Поясните в чем разница между весом неподвижного тела и движущегося с ускорением. 11.Когда возникает невесомость? Приведите примеры. 12.Какие силы называют силами упругости? Сформулируйте закон Гука. 13.Какие взаимодействия определяют силу трения? Сформулируйте определение силы трения, перечислите возможные виды трения. 14.Чему равна сила трения покоя? Как находится максимальная сила трения покоя и от чего она зависит? 15.Трактор сила тяги которого на крюке 15 кН, сообщает прицепу ускорение 0,5 м/с2. Какое ускорение сообщит такому же прицепу трактор, развивающий тяговое усилие 60 кН. 16.Тело массой 4 кг под действием некоторой силы приобрело ускорение 2 м/с2. Какое ускорение приобретает тело массой 10 кг под действием такой же силы? 17.На тело массой 5кг действуют силы F1=9н и F2=12н, Направленные на север и восток соответственно. Чему равно и куда направлено ускорение тела? 18.Моторная лодка движется с ускорением 2 м/с2 под действием трех сил: силы тяги двигателя 1000Н, силы ветра 1000Н и силы сопротивления воды 414 Н. Первая сила направлена на юг, Вторая- на запад, а сила сопротивления воды - противоположна направлению движения лодки. В каком направлении движется лодка и чему равна её масса? 19.Найти удлинение буксирного троса с жесткостью 100кН/м при буксировке автомобиля массой 2 т с ускорением 0,5 м/с2. Трением принебречь. 20.Во сколько раз сила гравитационного притяжения двух шаров массой по 1 кг, находящихся на расстоянии 1м друг от друга, меньше силы их притяжения к Земле? 21.Каково натяжение троса лифта массой 1000кг при его движении с ускорением 1 м/с2, направленным вертикально вверх? 22.С каким ускорением будет двигаться тело массой 1,5 кг, если на него будет действовать сила 20Н, направленная под углом 300 к горизонту? Коэффициент трения тела о поверхность равен 0,2. 23.Наклонная плоскость, образующая угол 300 с плоскостью горизонта, имеет длину 2м. Тело, двигаясь равноускоренно, соскользнуло с этой плоскости за время 2с. Определить коэффициент трения тела о плоскость.
|
|
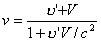 (1) представляет собой релятивистский закон. Преобразования скорости, что удовлетворяет всем необходимым требованиям специальной теории относительности.
(1) представляет собой релятивистский закон. Преобразования скорости, что удовлетворяет всем необходимым требованиям специальной теории относительности. .
.
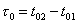
 O очевидно, что τ–>τ0.
O очевидно, что τ–>τ0.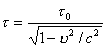 (2)
(2)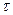 #
#  (1)
(1)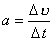 . Так как время действия тел друг на друга одинаково, изменение скорости больше у того тела, которое приобретает большее ускорение.
. Так как время действия тел друг на друга одинаково, изменение скорости больше у того тела, которое приобретает большее ускорение.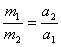 (2)
(2) (3). Отношение массы тела mт к массе эталона mэт равно отношению модуля ускорения эталона аэт к модулю ускорения тела ат при их взаимодействии. Масса тела может быть выражена через массу эталона:
(3). Отношение массы тела mт к массе эталона mэт равно отношению модуля ускорения эталона аэт к модулю ускорения тела ат при их взаимодействии. Масса тела может быть выражена через массу эталона:  . (4) Плотность вещества. Отношение массы m тела к его объему V называется плотностью вещества:
. (4) Плотность вещества. Отношение массы m тела к его объему V называется плотностью вещества: 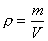 Плотность выражается в килограммах на кубический метр, единицей плотности.
Плотность выражается в килограммах на кубический метр, единицей плотности. Обобщая подобные наблюдения и опыты, И. Ньютон сформулировал один из основных законов механики: сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение:
Обобщая подобные наблюдения и опыты, И. Ньютон сформулировал один из основных законов механики: сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение: .Отсюда следует равенство: a1m1 = a2m2.
.Отсюда следует равенство: a1m1 = a2m2. В векторном виде это уравнение следует записать в виде:
В векторном виде это уравнение следует записать в виде: 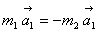 . Знак «минус» выражает тот опытный факт, что при взаимодействии тел их ускорения всегда имеют противоположные направления.
. Знак «минус» выражает тот опытный факт, что при взаимодействии тел их ускорения всегда имеют противоположные направления.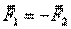 (6).
(6). , или
, или 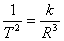 (7) Причины таких закономерностей движения планет пытался выяснить и сам Кеплер. Однако строгое научное объяснение планетных движений было дано лишь И. Ньютоном. Математическая запись закона для сил тяготения, действующих между Солнцем и планетами: сила тяготения пропорциональна массе Солнца и массе планеты и обратно пропорциональна квадрату расстояния между ними:
(7) Причины таких закономерностей движения планет пытался выяснить и сам Кеплер. Однако строгое научное объяснение планетных движений было дано лишь И. Ньютоном. Математическая запись закона для сил тяготения, действующих между Солнцем и планетами: сила тяготения пропорциональна массе Солнца и массе планеты и обратно пропорциональна квадрату расстояния между ними: 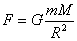 (8).
(8). (9),
(9), Самый простой случай движения тел под действием силы тяжести — свободное падение с начальной скоростью, равной нулю. В этом случае тело движется прямолинейно с ускорением свободного падения по направлению к центру Земли. Если начальная скорость тела отлична от нуля и вектор начальной скорости направлен не по вертикали, то тело под действием силы тяжести движется с ускорением свободного падения по криволинейной траектории. Форму такой траектории наглядно иллюстрирует струя воды, вытекающая под некоторым углом к горизонту. Скорость, с которой происходит движение тела по круговой орбите под действием силы всемирного тяготения, называется первой космической скоростью. Определим первую космическую скорость для Земли. Если тело под действием силы тяжести движется вокруг Земли равномерно по окружности радиусом R, то ускорение свободного падения является его центростремительным ускорением:
Самый простой случай движения тел под действием силы тяжести — свободное падение с начальной скоростью, равной нулю. В этом случае тело движется прямолинейно с ускорением свободного падения по направлению к центру Земли. Если начальная скорость тела отлична от нуля и вектор начальной скорости направлен не по вертикали, то тело под действием силы тяжести движется с ускорением свободного падения по криволинейной траектории. Форму такой траектории наглядно иллюстрирует струя воды, вытекающая под некоторым углом к горизонту. Скорость, с которой происходит движение тела по круговой орбите под действием силы всемирного тяготения, называется первой космической скоростью. Определим первую космическую скорость для Земли. Если тело под действием силы тяжести движется вокруг Земли равномерно по окружности радиусом R, то ускорение свободного падения является его центростремительным ускорением: 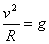 (11).
(11). (12)
(12)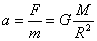 (13).
(13). = -
= -  . (14)
. (14)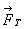 = -
= - 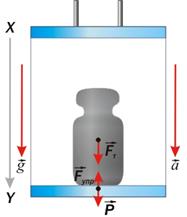 При ускоренном движении тела и опоры вес P будет отличаться от силы тяжести FT. По второму закону Ньютона, при движении тела массой m под действием силы тяжести FT и силы упругости Fупр с ускорением а выполняется равенство:
При ускоренном движении тела и опоры вес P будет отличаться от силы тяжести FT. По второму закону Ньютона, при движении тела массой m под действием силы тяжести FT и силы упругости Fупр с ускорением а выполняется равенство: 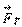 +
+ 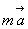 . (17). Из уравнений для веса P получаем:
. (17). Из уравнений для веса P получаем:  (18) или
(18) или 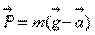 (19).
(19).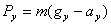 . Так как проекции векторов положительны и параллельны координатной оси, их можно заменить модулями векторов: P = m(g - a). Вес тела, направление ускорения которого совпадает с направлением ускорения свободного падения, меньше веса покоящегося тела.
. Так как проекции векторов положительны и параллельны координатной оси, их можно заменить модулями векторов: P = m(g - a). Вес тела, направление ускорения которого совпадает с направлением ускорения свободного падения, меньше веса покоящегося тела.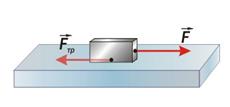 Сила упругости. Вблизи поверхности Земли любое тело действует сила тяжести, однако, большинство тел вокруг нас не падают с ускорением, а находятся в покое. Неподвижны книга, лежащая на столе, и стол, стоящий на полу. Книга на столе неподвижна — значит, кроме силы тяжести на нее действуют другие силы и равнодействующая всех сил равна нулю. Сила, возникающая в результате деформации тела и направленная в сторону, противоположную перемещениям частиц тела при деформации, называется силой упругости. Опыты по растяжению и сжатию твердых стержней показали, что при малых по сравнению с размерами тел деформациях модуль силы упругости пропорционален модулю вектора перемещения свободного конца стержня. Направление вектора силы упругости противоположно направлению вектора перемещения при деформации. Поэтому для проекции силы упругости на ось ОХ, направленную по вектору перемещения, выполняется равенство: (Fупр)x = -kx, (20) где x — удлинение стержня. Связь между проекцией силы упругости и удлинением тела была установлена экспериментально английским ученым Робертом Гуком (1635—1703) и поэтому называется законом Гука: Сила упругости, возникающая при деформации тела, прямо пропорциональна удлинению тела и направлена в сторону, противоположную направлению перемещений частиц тела при деформации. Коэффициент пропорциональности k в законе Гука называется жесткостью тела. Жесткость тела зависит от формы и размеров тела и от материала, из которого оно изготовлено. Жесткость в СИ выражается в ньютонах на метр (Н/м). Выясним природу сил упругости. В состав атомов и молекул входят частицы, обладающие электрическими зарядами. Атомы в твердом теле расположены таким образом, что силы отталкивания одноименных электрических зарядов и притяжения разноименных зарядов уравновешивают друг друга. При изменениях взаимных положений атомов или молекул в твердом теле в результате его деформации электрические силы стремятся возвратить атомы в первоначальное положение. Так при деформации возникает сила упругости. Силы взаимодействия электрических зарядов называются электромагнитными силами. Так как силы упругости обусловлены взаимодействиями электрических зарядов, по своей природе они являются электромагнитными силами.
Сила упругости. Вблизи поверхности Земли любое тело действует сила тяжести, однако, большинство тел вокруг нас не падают с ускорением, а находятся в покое. Неподвижны книга, лежащая на столе, и стол, стоящий на полу. Книга на столе неподвижна — значит, кроме силы тяжести на нее действуют другие силы и равнодействующая всех сил равна нулю. Сила, возникающая в результате деформации тела и направленная в сторону, противоположную перемещениям частиц тела при деформации, называется силой упругости. Опыты по растяжению и сжатию твердых стержней показали, что при малых по сравнению с размерами тел деформациях модуль силы упругости пропорционален модулю вектора перемещения свободного конца стержня. Направление вектора силы упругости противоположно направлению вектора перемещения при деформации. Поэтому для проекции силы упругости на ось ОХ, направленную по вектору перемещения, выполняется равенство: (Fупр)x = -kx, (20) где x — удлинение стержня. Связь между проекцией силы упругости и удлинением тела была установлена экспериментально английским ученым Робертом Гуком (1635—1703) и поэтому называется законом Гука: Сила упругости, возникающая при деформации тела, прямо пропорциональна удлинению тела и направлена в сторону, противоположную направлению перемещений частиц тела при деформации. Коэффициент пропорциональности k в законе Гука называется жесткостью тела. Жесткость тела зависит от формы и размеров тела и от материала, из которого оно изготовлено. Жесткость в СИ выражается в ньютонах на метр (Н/м). Выясним природу сил упругости. В состав атомов и молекул входят частицы, обладающие электрическими зарядами. Атомы в твердом теле расположены таким образом, что силы отталкивания одноименных электрических зарядов и притяжения разноименных зарядов уравновешивают друг друга. При изменениях взаимных положений атомов или молекул в твердом теле в результате его деформации электрические силы стремятся возвратить атомы в первоначальное положение. Так при деформации возникает сила упругости. Силы взаимодействия электрических зарядов называются электромагнитными силами. Так как силы упругости обусловлены взаимодействиями электрических зарядов, по своей природе они являются электромагнитными силами. = -
= -  .
. Коэффициент трения. Опыт показывает, что: 1) максимальное значение силы трения покоя не зависит от площади поверхности соприкосновения тел. 2) максимальное значение модуля силы трения покоя прямо пропорционально силе нормального давления. Взаимодействие тела и опоры вызывает деформацию и тела, и опоры.
Коэффициент трения. Опыт показывает, что: 1) максимальное значение силы трения покоя не зависит от площади поверхности соприкосновения тел. 2) максимальное значение модуля силы трения покоя прямо пропорционально силе нормального давления. Взаимодействие тела и опоры вызывает деформацию и тела, и опоры.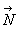 . Поэтому предыдущий вывод можно сформулировать так: модуль максимальной силы трения покоя пропорционален силе реакции опоры:
. Поэтому предыдущий вывод можно сформулировать так: модуль максимальной силы трения покоя пропорционален силе реакции опоры:  . Греческой буквой μ обозначен коэффициент пропорциональности, называемый коэффициентом трения.
. Греческой буквой μ обозначен коэффициент пропорциональности, называемый коэффициентом трения.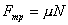 (21)
(21)